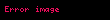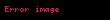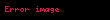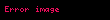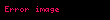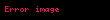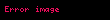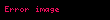Heron formülü, kenar uzunlukları bilinen bir üçgenin alanını hesaplamaya yarayan geometri formülüdür. Yunan matematikçi Heron tarafından bulunmuştur.

s, üçgenin göstermektedir:
Heron formülü şu şekillerde de yazılabilir:
Örnek
ΔABC, kenar uzunlukları a=7, b=4 ve c=5 olan bir üçgen olsun. Yarıçevre 
İspatı
Kosinüs teoremini yazarsak,
C açısının sinüsünü bulalım
Üçgenin a kenarının yüksekliği b·sin(C) olur.
İspatın iki adımında, kullanılmıştır.
Kaynakça
- "Heron's Formula". Mathworld. 5 Eylül 2015 tarihinde kaynağından . Erişim tarihi: 7 Ekim 2013.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Heron formulu kenar uzunluklari bilinen bir ucgenin alanini hesaplamaya yarayan geometri formuludur Yunan matematikci Heron tarafindan bulunmustur Kenar uzunluklari a b ve c olan bir ucgen A s s a s b s c displaystyle A sqrt s s a s b s c s ucgenin gostermektedir s a b c2 displaystyle s frac a b c 2 Heron formulu su sekillerde de yazilabilir A 14 a b c a b c a b c a b c displaystyle A frac 1 4 sqrt a b c a b c a b c a b c A 142 a2b2 a2c2 b2c2 a4 b4 c4 displaystyle A frac 1 4 sqrt 2 a 2 b 2 a 2 c 2 b 2 c 2 a 4 b 4 c 4 A 14 a2 b2 c2 2 2 a4 b4 c4 displaystyle A frac 1 4 sqrt a 2 b 2 c 2 2 2 a 4 b 4 c 4 A 144a2b2 a2 b2 c2 2 displaystyle A frac 1 4 sqrt 4a 2 b 2 a 2 b 2 c 2 2 OrnekDABC kenar uzunluklari a 7 b 4 ve c 5 olan bir ucgen olsun Yaricevre s 12 a b c 12 7 4 5 8 displaystyle s tfrac 1 2 a b c tfrac 1 2 7 4 5 8 ve alan T s s a s b s c 8 8 7 8 4 8 5 displaystyle T sqrt s left s a right left s b right left s c right sqrt 8 cdot 8 7 cdot 8 4 cdot 8 5 8 1 4 3 96 46 9 8 displaystyle sqrt 8 cdot 1 cdot 4 cdot 3 sqrt 96 4 sqrt 6 approx 9 8 dd IspatiKosinus teoremini yazarsak cos C a2 b2 c22ab displaystyle cos widehat C frac a 2 b 2 c 2 2ab C acisinin sinusunu bulalim sin C 1 cos2 C 4a2b2 a2 b2 c2 22ab displaystyle sin widehat C sqrt 1 cos 2 widehat C frac sqrt 4a 2 b 2 a 2 b 2 c 2 2 2ab Ucgenin a kenarinin yuksekligi b sin C olur A 12 taban yukseklik 12absin C 144a2b2 a2 b2 c2 2 14 2ab a2 b2 c2 2ab a2 b2 c2 14 c2 a b 2 a b 2 c2 c a b c a b a b c a b c 16 b c a 2 a c b 2 a b c 2 a b c 2 a b c 2 b c a 2 a c b 2 a b c 2 s s a s b s c displaystyle begin aligned A amp frac 1 2 mbox taban mbox yukseklik amp frac 1 2 ab sin widehat C amp frac 1 4 sqrt 4a 2 b 2 a 2 b 2 c 2 2 amp frac 1 4 sqrt 2ab a 2 b 2 c 2 2ab a 2 b 2 c 2 amp frac 1 4 sqrt c 2 a b 2 a b 2 c 2 amp sqrt frac c a b c a b a b c a b c 16 amp sqrt frac b c a 2 frac a c b 2 frac a b c 2 frac a b c 2 amp sqrt frac a b c 2 frac b c a 2 frac a c b 2 frac a b c 2 amp sqrt s left s a right left s b right left s c right end aligned Ispatin iki adiminda kullanilmistir Kaynakca Heron s Formula Mathworld 5 Eylul 2015 tarihinde kaynagindan Erisim tarihi 7 Ekim 2013
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State