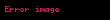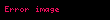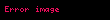Karmaşık analizde kalıntı veya rezidü, bir meromorf fonksiyonun bir tekillik etrafındaki çizgi integrallerinin davranışını açıklayan bir karmaşık sayıdır. Kalıntılar oldukça kolay bir şekilde hesaplanabilir ve bilindiklerinde kalıntı teoremi sayesinde çok karışık gerçel integrallerin belirlenmesi yolunu açarlar.
Tanım
Meromorf bir 





Motivasyon
Örnek olarak, C 'nin 0 civarında olduğu
integralini ele alalım.
Bu integrali elimizde var olan standard integral teoremlerini kullanmadan bulalım. ez 'nin Taylor serisini bildiğimiz için, bunu integrali alınan ifadeye (integranda) koyalım. O zaman integral
halini alır. 1/z5 'i de içeriye atarsak, integral şu hale gelir:

Şimdi integral daha basit bir biçim aldı.
olduğunu hatırlayalım. Böylece, cz−1 biçiminde olmayan her terimin C etrafındaki integrali sıfır olur ve integral de şu hale gelir:
1/4! değeri ez/z5 'in z = 0 'daki kalıntısıdır ve şu hallerde gösterilir.
Karmaşık düzlemde D = {z : 0 < |z - c| < R} verilmiş olsun ve f de (en azından) D üzerinde holomorf bir fonksiyon olsun. f nin c noktasındaki kalıntısı olan Res(f, c), f 'nin c noktasındaki Laurent serisi açılımında (z - c)−1 ifadesinin a-1 katsayısıdır. Bir basit kutupta, kalıntı
ile verilir.
Cauchy integral formülüne göre,
olmaktadır. Burada γ, c etrafında saat yönünün tersine yönde bir çember çizmektedir. γ'yı c etrafında istediğimiz kadar küçük yapabileceğimiz bir ε yarıçaplı çember olarak seçebiliriz.
g ve h 'nin c 'nin bir komşuluğunda h(c) = 0 ve g(c) ≠ 0 olacak şekilde holomorf fonksiyonlar olduğu f(z)=g(z)/h(z) fonksiyonunun bir c basit kutbundaki kalıntısı
ile verilir. Daha genel olarak, f 'nin mertebesi n olan bir z = c kutbundaki kalıntısı
formülü ile bulunabilir.
Eğer fonksiyon { z : |z - c| < R } diskinde holomorf olan bir fonksiyona devam ettirelebiliyorsa, o zaman Res(f, c) = 0 olur. Bunun tersi de genel de doğru değildir.
En son formül, düşük mertebeli kutuplardaki kalıntıları bulmak için faydalı olabilir. Yüksek mertebeli kutuplar için seri açılımını kullanmak daha kolaydır.
Seri yöntemleri
Bir fonksiyonun bir parçası veya tümü Taylor serisi veya Laurent serisi şeklinde açılabiliyorsa, o zaman kalıntıyı hesaplamak diğer yöntemlerden epeyce daha kolaydır.
Örnek olarak, bazı belli kontür integrallerini bulmaya yarayabilecek,
fonksiyonunun tekilliklerindeki kalıntılarını bulalım. Bu fonksiyonun açık bir şekilde z = 0 noktasında tekilliği vardır. Bununla birlikte, payda çarpanlarına ayrılıp
şeklinde yazılırsa, bu tekilliğin kaldırılabilir tekillik olduğu açıktır ve bu yüzden bu z = 0 noktasındaki kalıntı 0'dır.
Diğer tek tekillik ise z = 1 noktasındadır. Bir g(z) fonksiyonunun z = a noktasındaki Taylor serisinin ifadesinin
olduğunu hatırlayalım. O zaman, g(z) = sin z ve a = 1 için şunu yazabiliriz:
Ayrıca, g(z) = 1/z ve a = 1 için
yazabiliriz.
Bu iki seriyi çarparak ve 1/(z - 1) ifadesini koyarak
açılımını elde ederiz. Böylece, f(z) 'nin z = 1 noktasındaki kalıntısı sin 1 olur.
Notlar
- ^ Türkçe notasyonda Rez(f,a) da kullanılır; ancak genelde karmaşık değişkenler için z harfi kullanıldığından, bu gösterim karmaşaya yol açmaktadır.
Ayrıca bakınız
Dış bağlantılar
- Eric W. Weisstein, Karmaşık Kalıntı (MathWorld)
Kaynakça
- Ahlfors, Lars (1979), Complex Analysis, McGraw Hill
- Marsden & Hoffman, Basic complex analysis (Freeman, 1999).
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Karmasik analizde kalinti veya rezidu bir meromorf fonksiyonun bir tekillik etrafindaki cizgi integrallerinin davranisini aciklayan bir karmasik sayidir Kalintilar oldukca kolay bir sekilde hesaplanabilir ve bilindiklerinde kalinti teoremi sayesinde cok karisik gercel integrallerin belirlenmesi yolunu acarlar TanimMeromorf bir f displaystyle f fonksiyonunun korunmali bir a displaystyle a tekilligindeki kalintisi ki genelde Res f a displaystyle Res f a ile gosterilir f z R z a displaystyle f z R over z a ifadesini 0 lt z a lt d displaystyle 0 lt z a lt delta analitik sahip yapan biricik R displaystyle R degeridir Donusumlu olarak kalinitilar bazen Laurent serisi acilimlari bulunarak da hesaplanabilir ve bazen de bu seri acilimlari baglaminda tanimlanirlar MotivasyonOrnek olarak C nin 0 civarinda oldugu Cezz5dz displaystyle oint C e z over z 5 dz integralini ele alalim Bu integrali elimizde var olan standard integral teoremlerini kullanmadan bulalim ez nin Taylor serisini bildigimiz icin bunu integrali alinan ifadeye integranda koyalim O zaman integral C1z5 1 z z22 z33 z44 z55 z66 dz displaystyle oint C 1 over z 5 left 1 z z 2 over 2 z 3 over 3 z 4 over 4 z 5 over 5 z 6 over 6 cdots right dz halini alir 1 z5 i de iceriye atarsak integral su hale gelir C 1z5 zz5 z22 z5 z33 z5 z44 z5 z55 z5 z66 z5 dz displaystyle oint C left 1 over z 5 z over z 5 z 2 over 2 z 5 z 3 over 3 z 5 z 4 over 4 z 5 z 5 over 5 z 5 z 6 over 6 z 5 cdots right dz C 1z5 1z4 12 z3 13 z2 14 z 15 z6 dz displaystyle oint C left 1 over z 5 1 over z 4 1 over 2 z 3 1 over 3 z 2 1 over 4 z 1 over 5 z over 6 cdots right dz Simdi integral daha basit bir bicim aldi C1zadz 0 a Z a 1 displaystyle oint C 1 over z a dz 0 quad a in mathbb Z mbox a neq 1 oldugunu hatirlayalim Boylece cz 1 biciminde olmayan her terimin C etrafindaki integrali sifir olur ve integral de su hale gelir C14 zdz 14 C1zdz 14 2pi pi12 displaystyle oint C 1 over 4 z dz 1 over 4 oint C 1 over z dz 1 over 4 2 pi i pi i over 12 1 4 degeri ez z5 in z 0 daki kalintisidir ve su hallerde gosterilir Res0ezz5 veya Resz 0ezz5 veya Res f 0 displaystyle mathrm Res 0 e z over z 5 mathrm veya mathrm Res z 0 e z over z 5 mathrm veya mathrm Res f 0 Karmasik duzlemde D z 0 lt z c lt R verilmis olsun ve f de en azindan D uzerinde holomorf bir fonksiyon olsun f nin c noktasindaki kalintisi olan Res f c f nin c noktasindaki Laurent serisi aciliminda z c 1 ifadesinin a 1 katsayisidir Bir basit kutupta kalinti Res f c limz c z c f z displaystyle operatorname Res f c lim z to c z c f z ile verilir Cauchy integral formulune gore Res f c 12pi gf z dz displaystyle operatorname Res f c 1 over 2 pi i int gamma f z dz olmaktadir Burada g c etrafinda saat yonunun tersine yonde bir cember cizmektedir g yi c etrafinda istedigimiz kadar kucuk yapabilecegimiz bir e yaricapli cember olarak secebiliriz g ve h nin c nin bir komsulugunda h c 0 ve g c 0 olacak sekilde holomorf fonksiyonlar oldugu f z g z h z fonksiyonunun bir c basit kutbundaki kalintisi Res f c g c h c displaystyle operatorname Res f c frac g c h c ile verilir Daha genel olarak f nin mertebesi n olan bir z c kutbundaki kalintisi Res f c 1 n 1 limz c ddz n 1 f z z c n displaystyle mathrm Res f c frac 1 n 1 cdot lim z to c left frac d dz right n 1 left f z cdot z c n right formulu ile bulunabilir Eger fonksiyon z z c lt R diskinde holomorf olan bir fonksiyona devam ettirelebiliyorsa o zaman Res f c 0 olur Bunun tersi de genel de dogru degildir En son formul dusuk mertebeli kutuplardaki kalintilari bulmak icin faydali olabilir Yuksek mertebeli kutuplar icin seri acilimini kullanmak daha kolaydir Seri yontemleri Bir fonksiyonun bir parcasi veya tumu Taylor serisi veya Laurent serisi seklinde acilabiliyorsa o zaman kalintiyi hesaplamak diger yontemlerden epeyce daha kolaydir Ornek olarak bazi belli kontur integrallerini bulmaya yarayabilecek f z sin zz2 z displaystyle f z sin z over z 2 z fonksiyonunun tekilliklerindeki kalintilarini bulalim Bu fonksiyonun acik bir sekilde z 0 noktasinda tekilligi vardir Bununla birlikte payda carpanlarina ayrilip f z sin zz z 1 displaystyle f z sin z over z z 1 seklinde yazilirsa bu tekilligin kaldirilabilir tekillik oldugu aciktir ve bu yuzden bu z 0 noktasindaki kalinti 0 dir Diger tek tekillik ise z 1 noktasindadir Bir g z fonksiyonunun z a noktasindaki Taylor serisinin ifadesinin g z g a g a z a g a z a 22 g a z a 33 displaystyle g z g a g a z a g a z a 2 over 2 g a z a 3 over 3 cdots oldugunu hatirlayalim O zaman g z sin z ve a 1 icin sunu yazabiliriz sin z sin 1 cos 1 z 1 sin 1 z 1 22 cos 1 z 1 33 displaystyle sin z sin 1 cos 1 z 1 sin 1 z 1 2 over 2 cos 1 z 1 3 over 3 cdots Ayrica g z 1 z ve a 1 icin 1z 1 z 1 1 1 z 1 z 1 2 z 1 3 displaystyle frac 1 z frac 1 z 1 1 1 z 1 z 1 2 z 1 3 cdots yazabiliriz Bu iki seriyi carparak ve 1 z 1 ifadesini koyarak sin zz z 1 sin 1z 1 cos 1 sin 1 z 1 sin 12 cos 1 sin 1 displaystyle frac sin z z z 1 sin 1 over z 1 cos 1 sin 1 z 1 left frac sin 1 2 cos 1 sin 1 right cdots acilimini elde ederiz Boylece f z nin z 1 noktasindaki kalintisi sin 1 olur Notlar Turkce notasyonda Rez f a da kullanilir ancak genelde karmasik degiskenler icin z harfi kullanildigindan bu gosterim karmasaya yol acmaktadir Ayrica bakinizCauchy integral formulu Cauchy integral teoremi Kontur integrali yontemleri Morera teoremiDis baglantilarEric W Weisstein Karmasik Kalinti MathWorld KaynakcaAhlfors Lars 1979 Complex Analysis McGraw Hill Marsden amp Hoffman Basic complex analysis Freeman 1999
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans