Matematikte bir seri veya integral mutlak yakınsak olmayıp halen yakınsak ise koşullu yakınsak olur.
Tanım
Diğer bir deyişle bir reel sayı dizisi 

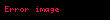
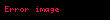

Alterne harmonik seri ise klasik bir örnektir

 'ye yakınsar ama mutlak yakınsak değildir (bkz. Harmonik seriler).
'ye yakınsar ama mutlak yakınsak değildir (bkz. Harmonik seriler). Bernhard Riemann, koşullu yakınsak bir serinin yeniden düzenlenerek herhangi bir değere (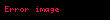
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir seri veya integral mutlak yakinsak olmayip halen yakinsak ise kosullu yakinsak olur TanimDiger bir deyisle bir reel sayi dizisi n 0 an textstyle sum n 0 infty a n in kosullu yakinsak olmasi icin limm n 0man textstyle lim m rightarrow infty sum n 0 m a n limitinin var olmasi gerekir sonsuz olmayan gercek bir sayi olarak yani displaystyle infty veya displaystyle infty olmayan ayrica n 0 an textstyle sum n 0 infty left a n right infty olmalidir Alterne harmonik seri ise klasik bir ornektir1 12 13 14 15 n 1 1 n 1n displaystyle 1 1 over 2 1 over 3 1 over 4 1 over 5 cdots sum limits n 1 infty 1 n 1 over n bu seri ln 2 displaystyle ln 2 ye yakinsar ama mutlak yakinsak degildir bkz Harmonik seriler Bernhard Riemann kosullu yakinsak bir serinin yeniden duzenlenerek herhangi bir degere displaystyle infty ve displaystyle infty dahil yakinsamasinin saglanabilecegini kanitladi Ayrica bakinizMutlak yakinsama
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans