Karekök ortalama; matematikte root mean square (kısaltması RMS ya da rms) ayrıca kuadratik ortalama olarak da bilinir. Değişen miktarların büyüklüğünün ölçülmesinde kullanılan istatistik bir ölçüttür. Değişimin artı ve eksi yönde olduğu dalgalarda özellikle çok faydalıdır.
Sürekli olarak değişen bir fonksiyonun sürekli olmayan değer serisi için hesaplanabilir. Karekök ortalama ismi karelerin ortalamasının karekökünün alınmasından gelir.
Tanım




Karekök ortalama hesaplanması

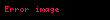
olarak hesaplanır.

Bir periyodik fonksiyonun RMS değeri fonsiyonun bir periyodunun RMS değerine eşittir. Sürekli bir fonksiyonun ya da sinyalin RMS değeri eşit aralıklarla bir dizi RMS değeri örneklenerek yaklaşık olarak hesaplanabilir.
Kullanım yerleri
Bir fonksiyonun RMS değeri çoğunlukla fizik ve elektrik mühendisliğinde kullanılır. Örneğin, 


Ancak akım değişen bir 
(
aritmetik ortalamayı ifade eder)
(R bir sabit olduğuna göre ortalamanın dışına çıkarılabilir)
(RMS in tanımından)
Aynı metot ile;
Ancak bu tanım ve akımın birbiriyle orantılı olduğu (yani yükün olduğu) varsayımı temel alınarak yapılmıştır ve genellenemez.
Şebeke güçlerinde olduğu gibi genel durumunda, 


Trigonometrik fonksiyonun karesinin alınmasını elimine etmek için trigonometrik bir varlık kullanıldığında:
Fakat T2 ve T1 zamanlarında sinüs tam bir döngü tamamladığı yani aynı değerlere geldiği için için sinüs değerler birbirini götürür ve geriye aşağıdaki ifade kalır.
Saf bir sinüs dalgası için; tepe voltajı = RMS voltajı x 1.414(
Dönüşüm katsayıları
- Tepe genliği
tepeden tepeye genliğin
yarısıdır.
- Bir dalga formunun zirve faktörü (crest factor); tepe(zirve) değerinin RMS değerine oranıdır.
- Bir AC dalga formunun şekil faktörü (form factor); tepe(zirve) değerinin ortalama değerine oranıdır.
Sinüs dalga için;
- RMS değeri = 0.707 x Tepe değeri
- Ortalama Değeri = 0.637 x Tepe değeri
- Tepeden tepeye değeri = 2 x Tepe değeri
Kare dalga için;
- RMS değeri = Tepe değeri
- Ortalama Değeri = (Tepe değeri x Darbe süresi) / Periyot
- Tepeden tepeye değeri = 2 x Tepe değeri
Üçgen dalga için;
- RMS değeri = 0.577 x Tepe değeri
- Ortalama Değeri = 0.33 x Tepe değeri
- Tepeden tepeye değeri = 2 x Tepe değeri
Dış bağlantılar
- RMS calculator2 Ocak 2010 tarihinde Wayback Machine sitesinde .
- An explanation of why RMS is a misnomer when applied to power30 Ağustos 2009 tarihinde Wayback Machine sitesinde .
- RMS, Peak and Average for some waveforms12 Ocak 2010 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Karekok ortalama matematikte root mean square kisaltmasi RMS ya da rms ayrica kuadratik ortalama olarak da bilinir Degisen miktarlarin buyuklugunun olculmesinde kullanilan istatistik bir olcuttur Degisimin arti ve eksi yonde oldugu dalgalarda ozellikle cok faydalidir Surekli olarak degisen bir fonksiyonun surekli olmayan deger serisi icin hesaplanabilir Karekok ortalama ismi karelerin ortalamasinin karekokunun alinmasindan gelir Tanimkg NiN 1 X100 displaystyle k text g left sqrt langle Ni over N rangle 1 right X100 k displaystyle k Kgort kg1 kg2 kg3 kgnn displaystyle K text gort left k text g1 k text g2 k text g3 ldots k text gn over n right Ng Ns 1 Kg100 tg ts displaystyle N text g N text s left 1 K text g over 100 right langle tg ts rangle Karekok ortalama hesaplanmasin displaystyle n sayidaki degerlerin x1 x2 xn displaystyle x 1 x 2 dots x n RMS degeri xrms 1n i 1nxi2 x12 x22 xn2n displaystyle x mathrm rms sqrt 1 over n sum i 1 n x i 2 sqrt x 1 2 x 2 2 cdots x n 2 over n olarak hesaplanir T1 t T2 displaystyle T 1 leq t leq T 2 araliginda surekli bir f t fonksiyonu icin karsilik gelen formulu frms 1T2 T1 T1T2 f t 2dt displaystyle f mathrm rms sqrt 1 over T 2 T 1 int T 1 T 2 f t 2 dt Bir periyodik fonksiyonun RMS degeri fonsiyonun bir periyodunun RMS degerine esittir Surekli bir fonksiyonun ya da sinyalin RMS degeri esit araliklarla bir dizi RMS degeri orneklenerek yaklasik olarak hesaplanabilir Kullanim yerleriBir fonksiyonun RMS degeri cogunlukla fizik ve elektrik muhendisliginde kullanilir Ornegin R displaystyle R direncindeki bir iletken tarafindan harcanan P displaystyle P gucunu hesaplamak isteyebiliriz Iletkenden sabit bir I displaystyle I akimi aktiginda bu hesabi yapmak kolaydir Basitce P I2R displaystyle P I 2 R Ancak akim degisen bir I t displaystyle I t fonksiyonu ise burada rms degeri devreye girer Pavg displaystyle P mathrm avg I2R displaystyle langle I 2 R rangle displaystyle langle ldots rangle aritmetik ortalamayi ifade eder R I2 displaystyle R langle I 2 rangle R bir sabit olduguna gore ortalamanin disina cikarilabilir Irms2R displaystyle I mathrm rms 2 R RMS in tanimindan Ayni metot ile Pavg Vrms2R displaystyle P mathrm avg V mathrm rms 2 over R Pavg VrmsIrms displaystyle P mathrm avg V mathrm rms I mathrm rms Ancak bu tanim ve akimin birbiriyle orantili oldugu yani yukun oldugu varsayimi temel alinarak yapilmistir ve genellenemez Sebeke guclerinde oldugu gibi genel durumunda I t displaystyle I t sinusoidal akim oldugunda rms degeri yukaridaki surekli durum denkleminden kolaylikla hesaplanabilir Ip displaystyle I mathrm p yi tepe genligi olarak tanimladigimizda Irms 1T2 T1 T1T2 Ipsin wt 2dt displaystyle I mathrm rms sqrt 1 over T 2 T 1 int T 1 T 2 I mathrm p sin omega t 2 dt Ip displaystyle I mathrm p positif bir gercek sayi olduguna gore Irms Ip1T2 T1 T1T2sin2 wt dt displaystyle I mathrm rms I mathrm p sqrt 1 over T 2 T 1 int T 1 T 2 sin 2 omega t dt Trigonometrik fonksiyonun karesinin alinmasini elimine etmek icin trigonometrik bir varlik kullanildiginda Irms Ip1T2 T1 T1T21 cos 2wt 2dt displaystyle I mathrm rms I mathrm p sqrt 1 over T 2 T 1 int T 1 T 2 1 cos 2 omega t over 2 dt Irms Ip1T2 T1 t2 sin 2wt 4w T1T2 displaystyle I mathrm rms I mathrm p sqrt 1 over T 2 T 1 left t over 2 sin 2 omega t over 4 omega right T 1 T 2 Fakat T2 ve T1 zamanlarinda sinus tam bir dongu tamamladigi yani ayni degerlere geldigi icin icin sinus degerler birbirini goturur ve geriye asagidaki ifade kalir Irms Ip1T2 T1 t2 T1T2 Ip1T2 T1T2 T12 Ip2 displaystyle I mathrm rms I mathrm p sqrt 1 over T 2 T 1 left t over 2 right T 1 T 2 I mathrm p sqrt 1 over T 2 T 1 T 2 T 1 over 2 I mathrm p over sqrt 2 Saf bir sinus dalgasi icin tepe voltaji RMS voltaji x 1 414 2 displaystyle sqrt 2 tur Tepeden tepeye voltaji bunun iki katidir Donusum katsayilariTepe genligi Ip displaystyle I mathrm p tepeden tepeye genligin Ip p displaystyle I mathrm p p yarisidir Bir dalga formunun zirve faktoru crest factor tepe zirve degerinin RMS degerine oranidir Bir AC dalga formunun sekil faktoru form factor tepe zirve degerinin ortalama degerine oranidir Sinus dalga icin RMS degeri 0 707 x Tepe degeri Ortalama Degeri 0 637 x Tepe degeri Tepeden tepeye degeri 2 x Tepe degeriKare dalga icin RMS degeri Tepe degeri Ortalama Degeri Tepe degeri x Darbe suresi Periyot Tepeden tepeye degeri 2 x Tepe degeriUcgen dalga icin RMS degeri 0 577 x Tepe degeri Ortalama Degeri 0 33 x Tepe degeri Tepeden tepeye degeri 2 x Tepe degeriDis baglantilarRMS calculator2 Ocak 2010 tarihinde Wayback Machine sitesinde An explanation of why RMS is a misnomer when applied to power30 Agustos 2009 tarihinde Wayback Machine sitesinde RMS Peak and Average for some waveforms12 Ocak 2010 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State