Aritmetik ortalama

Aritmetik ortalama, bir sayı dizisindeki elemanların toplamının eleman sayısına bölünmesi ile elde edilir. İstatistik bilim dalında hem betimsel istatistik alanında hem de çıkarımsal istatistik alanında en çok kullanan merkezi eğilim ölçüsü' dür.

Aritmetik ortalama tahterevallisi

Tanımlama

Aritmetik ortalama matematiksel biçimde anakütle için μ ve örneklem için (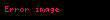${\displaystyle {\bar {x}}}$) olarak ifade edilir.

Genel formül

Aritmetik ortalama hesaplaması için kullanılan formüller, anakütle büyüklüğü N ve örneklem büyüklüğü n olduğu kabul edilirse, şöyle verilir: Anakütle aritmetik ortalaması:

${\displaystyle \mu ={\frac {1}{N}}\sum _{i=1}^{N}x_{i}={\frac {1}{N}}(x_{1}+\cdots +x_{N})}$

Örneklem aritmetik ortalaması:

${\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\cdots +x_{n})}$

Örneğin, bir sınıftaki farklı kişilerin aldığı not veya sayının toplamının kişi sayısına bölünmesi aritmetik ortalamayı verir.

Çokluk (frekans) dağılım verileri için formül gösterimi

Bazen veriler daha önceden özetlenip sınıflara ayrılıp gruplanmışlardır. Bu gruplanmış veri özetine çokluk dağılımı adı verilmektedir. Bu halde N veya n sayıda veri dizisi m sayıda gruba ayrılmakta ve her grup belli bir minimum ve maksimum değerler arasında bulunan verileri kapsamaktadır. Böylece veriler bir veya içinde m sayıda sınıf birinci sütunda ve her sınıf içinde bulunan çokluk (frekans) (${\displaystyle j=1,\cdots ,m}$ için ${\displaystyle f_{j})}$) ikinci sütunda yer almaktadır. Bu tür özetlenmiş veri dizisi için bir yaklaşık aritmetik ortalama bulunabilir. Bu yaklaşık bir değerdir çünkü her veri için gerçek x değeri değil, ancak sınıfsal ortalama (${\displaystyle j=1,\cdots ,m}$ için ${\displaystyle {\bar {x}}_{j}}$) kullanılmaktadır. Böylece çokluk dağılımlarında aritmetik ortalama hesaplanırken şu formüller kullanılır:
Anakütle ortalaması:

${\displaystyle \mu ={\frac {1}{N}}\sum _{j=1}^{m}{\bar {x}}_{j}f_{j}}$

Örneklem ortalamasi

${\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{j=1}^{m}{\bar {x}}_{j}f_{j}}$

Bazı Özellikleri

Aritmetik Ortalamanın bazı özellikleri aşağıdaki gibidir:

• ${\displaystyle \sum _{i=1}^{n}x_{i}=n{\bar {x}}}$
• ${\displaystyle {\frac {1}{n}}\sum _{i=1}^{n}cx_{i}=c{\bar {x}}}$
• ${\displaystyle \sum _{i=1}^{n}(x_{i}-{\bar {x}})=0}$
• ${\displaystyle \sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}$ minimumdur.

Dezavantajları

Aritmetik ortalama çok popüler olarak hesaplanıp kullanılmakla beraber bazı önemli dezavantajları bulunmaktadır.

• 'Aritmetik ortalama aşırı değerlere duyarlı bir merkezsel konum ölçüsüdür. Eğer veri dizisi için asimetrik olarak sadece bir uçsal değer ya aşırı küçük ya aşırı büyük ise aritmetik ortalama o aşırı değere yaklaşma gösterir.
• Aritmetik ortalama her türlü ölçülme ölçekli sayısal veri için kullanılamaz. (İsimsel ölçekli) sayısal veriler için aritmetik ortalama anlamsızdır. (Sırasal ölçekli) sayısal veriler için aritmetik ortalama kullanılması büyük tartışmalara açıktır. Birçok kişi değişik kişilerin sıralamalarının aynı olduğunu kabul etmedikleri için elde edilen verilerin toplamının ve bu toplamdan çıkartılan aritmetik ortalamanın anlamsız olacağını kabul etmektedirler. Ancak işletme alanı, davranışsal bilimler ve sosyal bilimlerde, özellikle anket verileri, sırasal ölçekli olmakta ve buna rağmen bu verilerin aritmetik ortalamaları pratikte onemli alanlarda kullanılmaktadır. (Aralıksal ölçekli) ve (oransal ölçekli) sayısal veriler için aritmetik ortalama anlamlıdır.

Ayrıca bakınız

• Merkezsel konum ölçüleri
• Geometrik ortalama
• Medyan
• Mod