Limit

Limit kelimesi Latince Limes ya da Limites 'den gelmekte olup sınır, uç nokta anlamındadır. Öklid ve Arşimet tarafından eğrisel kenarlara sahip şekillerle ilgili olan teoremlerde kullanılmıştır. Limit kavramı, çok önceleri kullanılmasına rağmen sonra unutulmuş ve daha sonra Newton ile Leibniz'in eserlerinde görülmüştür. Mesela, diferansiyel hesapta bir eğri (daire gibi) sonsuz küçük uzunlukta sonsuz kenara sahip bir çokgen olarak kabul edilir. Limit kavramından ortaya çıkan diferansiyel hesap, pek çok fizik probleminin kolayca ele alınmasını sağlar.

Matematiksel tanımı

f(x) fonksiyonu bir açık aralıkta tanımlanmış olsun ve L bir gerçek sayı olsun. Bütün 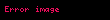${\displaystyle \varepsilon \ >0}$ değerleri için, bir ${\displaystyle \delta \ >0}$ bulunabiliyor, öyle ki bütün ${\displaystyle 0<|x-a|<\delta \ }$ sağlayan ${\displaystyle x}$ için, ${\displaystyle |f(x)-L|<\varepsilon \ }$ eşitsizliği doğru ise; L, f(x)'in a noktasındaki limitidir.

Bir fonksiyonun a'daki limiti (L):

${\displaystyle \lim _{x\to a}f(x)=L}$

şeklinde gösterilir.

Ve şöyle okunur "x a'ya giderken, f(x)'in limiti L'ye eşittir". x, a'ya yaklaşırken f(x) fonksiyonunun limit L'ye yaklaştığı sağ ok (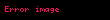${\displaystyle \rightarrow }$) ile gösterilir.

f(x) 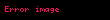${\displaystyle \rightarrow }$ L

1821’de Augustin Louis Cauchy, Karl Weierstrass’ı takiben yukarıdaki tanımlamadaki bir fonksiyonun limitinin tanımını şekillendirdi,19. Yüzyılda  limitin (ε,δ) tanımlamasıyla tanınan hale geldi. ε tanımının kullanımı(Yunanca küçük epsilon harfi) her küçük pozitif sayıyı gösterir. Böylece “f(x) isteğe bağlı olarak L’ye yakın olur”, sonuçta f(x) (L − ε, L + ε) aralığında yer alır demektir, aynı zamanda mutlak değer işareti kullanılarak da yazılabilir  |f(x) − L| < ε.”x c’ye yaklaşırken” ifadesi, baktığımız c’den uzak olan x’lerin bir  δ (Yunanca küçük delta harfi) pozitif sayısından küçük olduğunu gösterir. x’lerin  ya (c − δ, c) ya da (c, c + δ) içindeki değerleri 0 < |x − c| < δ ile ifade edilebilir. İkinci eşitsizlik x c’nin δ uzaklığı içinde olduğunu ifade ederken, ilk eşitsizlik x ve c arasındaki uzaklık 0’dan büyüktür ve x ≠ c demektir.

Yukarıdaki bir limitin tanımlamasının  f(c) ≠ L olsa bile doğru olduğunu unutmayalım. Gerçekten f fonksiyonunun c’de tanımlanmasına gerek yoktur.

${\displaystyle f(x)={\frac {x^{2}-1}{x-1}}}$

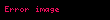
böyleyse f(1) tanımlanmaz (bkz. sıfır bölü sıfır), henüz x istenildiği kadar 1’e yakın hareket ederken, f(x) buna bağlı olarak 2’ye yaklaşıyor.

Böylece, x’i 1’e yeterince yaklaştırarak, f(x) 2’nin limitine istenildiği kadar yaklaştırılabilir.

Diğer bir deyişle,

${\displaystyle \lim _{x\to 1}{\frac {x^{2}-1}{x-1}}=2}$

Bu aynı zamanda cebirsel olarak da hesaplanabilir,

${\displaystyle {\frac {x^{2}-1}{x-1}}={\frac {(x+1)(x-1)}{x-1}}=x+1}$ her gerçek sayılar için x≠1.

Bundan beri x+1, 1’de x’in içinde süreklidir, şimdi x’e 1 yazabiliriz, böylece

${\displaystyle \lim _{x\to 1}{\frac {x^{2}-1}{x-1}}=1+1=2}$

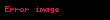
Sonsuz değerlerde limitlere ek olarak, fonksiyonların aynı zamanda sonsuzda limitleri vardır.

Örneğin, şunu dikkate alalım,

${\displaystyle f(x)={\frac {2x-1}{x}}}$

f(100)=1.9900

f(1000)=1.9990

f(10000)=1.99990

x aşırı büyüyünce, f(x)’in değeri 2’ye yaklaşıyor, ve f(x)’in değeri aynı zamanda istenirse sadece x’i yeterince büyük seçerek 2’ye tek olarak yakın yapılabilir. Bu durumda x sonsuza giderken f(x)’in limiti 2 olur. Matematiksel gösterimde,

${\displaystyle \lim _{x\to \infty }{\frac {2x-1}{x}}=2.}$

Dizilerin limiti

Şu diziyi ele alalım:  1.79, 1.799, 1.7999,... Dizinin limiti, sayılar 1,8’e “yaklaşıyor” olarak gözlenebilir.

Biçimsel olarak,  a₁, a₂, ... ‘yı gerçek sayılardan bir dizi olarak varsayalım. Dizinin limiti gerçek sayı L olarak belirtilebilir, şöyle ki;

${\displaystyle \lim _{n\to \infty }{a_{n}}=L}$

şöyle okunur

“n sonsuza giderken  a_n ‘in limiti L’ye eşittir”

şu anlama gelir

her gerçek sayı için ε > 0, her n>N için bir N doğal sayısı vardır. |a_n − L| < ε.

Sezgisel olarak, bu demek oluyor ki; mutlak değer |a_n – L| değeri, a_n ve L arasında olduğundan itibaren dizinin tüm elemanları limite istenildiği kadar yaklaşabilir. Her dizinin limiti vardır; eğer öyleyse ona yakınsak denir, eğer değilse ıraksaktır.

Önemli limitler

• ${\displaystyle \lim _{x\to \infty }(1+{\frac {k}{x}})^{x}=e^{k}}$
• ${\displaystyle \lim _{x\to 0}(1+x)^{\frac {k}{x}}=e^{k}}$
• ${\displaystyle \lim _{x\to 0}\cos(x)=1}$
• ${\displaystyle \lim _{x\to 0}{\frac {\sin(x)}{x}}=1}$
• ${\displaystyle \lim _{x\to 0}{\frac {\tan(x)}{x}}=1}$

Limit teoremleri

Eğer ${\displaystyle \lim _{x\to \infty }f(x)=a}$ ve ${\displaystyle \lim _{x\to \infty }g(x)=b}$ ise o zaman aşağıdaki denklemler doğrudur:

• ${\displaystyle \lim _{x\to \infty }(f(x)\pm g(x))=a\pm b}$
• ${\displaystyle \lim _{x\to \infty }(f(x)\cdot g(x))=a\cdot b}$
• ${\displaystyle \lim _{x\to \infty }{\frac {f(x)}{g(x)}}={\frac {a}{b}}}$, eğer ${\displaystyle b\neq 0}$.
• Eğer ${\displaystyle |f(x)|\leq |g(x)|}$ ve ${\displaystyle \lim _{x\to \infty }g(x)=0}$, o zaman ${\displaystyle \lim _{x\to \infty }f(x)=0}$.