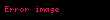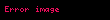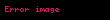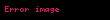Logaritmik dışbükey fonksiyon

Matematikte logaritma fonksiyonu ile bileşkesi dışbükey olan fonksiyonlara logaritmik dışbükey veya log dışbükey fonksiyon denir; daha matematiksel bir ifadeyle, verilmiş bir ${\displaystyle f}$ fonksiyonu için ${\displaystyle \log f}$ dışbükey bir fonksiyonsa, o zaman ${\displaystyle f}$ logaritmik dışbükey fonksiyondur.

Tanım

X gerçel bir vektör uzayınının dışbükey bir altkümesi olsun. f : X → R ise negatif olmayan değerler alan bir fonksiyon olsun. O zaman,

• ${\displaystyle {\log }\circ f}$ dışbükeyse, f logaritmik dışbükeydir.
• ${\displaystyle {\log }\circ f}$ kesin dışbükeyse, f kesin logaritmik dışbükeydir.

Burada, ${\displaystyle \log 0}$ değeri ${\displaystyle -\infty }$ olarak alınmıştır. Daha matematiksel bir ifadeyle açıkça yazmak gerekirse, f fonksiyonunun logaritmik dışbükeyliği ancak ve ancak x₁, x₂ ∈ X ve her t ∈ [0, 1] için aşağıdaki eşitsizlikleri sağlaması ile mümkündür:

${\displaystyle {\begin{aligned}\log f(tx_{1}+(1-t)x_{2})&\leq t\log f(x_{1})+(1-t)\log f(x_{2}),\\f(tx_{1}+(1-t)x_{2})&\leq f(x_{1})^{t}f(x_{2})^{1-t}.\end{aligned}}}$

Benzer bir şekilde, f fonksiyonunun kesin logaritmik dışbükeyliği ancak ve ancak yukarıdaki eşitsizliklerin bütün t ∈ (0, 1) için eşitlik olmadan sağlanması ile mümkündür.

Yukarıdaki tanıma göre, f sıfır değer alabilir. Ancak, f logaritmik dışbükeyse ve X kümesi içindeki herhangi bir noktada 0 değeri alıyorsa, o zaman Xin içindeki her noktada sıfır değeri almak zorundadır.

Denk koşullar

Eğer f bir I ⊆ R aralığında tanımlanmış ve türevlenebilir bir fonksiyonsa f fonksiyonunun logaritmik dışbükeyliği ancak ve ancak aşağıdaki eşitsizliğin I'daki her x ve y için sağlanmasıyla mümkündür.

${\displaystyle \log f(x)\geq \log f(y)+{\frac {f'(y)}{f(y)}}(x-y).}$

I'daki her x ve y için x > y varsayıldığında yukarıdaki eşitsizlik şuna denktir:

${\displaystyle \left({\frac {f(x)}{f(y)}}\right)^{\frac {1}{x-y}}\geq e^{\frac {f'(y)}{f(y)}}.}$

Benzer bir şekilde, f fonksiyonunun kesin logaritmik dışbükeyliği ancak ve ancak yukarıdaki eşitsizliklerin eşitlik olmadan sağlanması ile mümkündür.

Eğer f bir I ⊆ R aralığında tanımlanmış ve iki kere türevlenebilir bir fonksiyonsa, f fonksiyonunun logaritmik dışbükeyliği ancak ve ancak I'daki her x için

${\displaystyle f''(x)f(x)\geq f'(x)^{2}}$

olması ile mümkündür. Eğer eşitsizlik kâti ise, o zaman f fonksiyonu kesin logaritmik dışbükeydir. Ancak, bunun tersi doğru değildir; yani, f kesin logaritmik dışbükey olup bir x değeri için, ${\displaystyle f''(x)f(x)=f'(x)^{2}}$ olabilir. Örneğin, ${\displaystyle f(x)=e^{x^{4}}}$ ise, o zaman, f kesin logaritmik dışbükeydir. Ancak, ${\displaystyle f''(0)f(0)=0=f'(0)^{2}}$ olur.

Ayrıca, ${\displaystyle f\colon I\to (0,\infty )}$ fonksiyonunun logaritmik dışbükeyliği ancak ve ancak ${\displaystyle \alpha \in \mathbb {R} }$ için ${\displaystyle e^{\alpha x}f(x)}$ fonksiyonunun dışbükey olması ile mümkündür.

Yeterli koşullar

• ${\displaystyle f_{1},\ldots ,f_{n}}$ logaritmik dışbükeyse ve ${\displaystyle w_{1},\ldots ,w_{n}}$ negatif olmayan gerçel sayılarsa ${\displaystyle f_{1}^{w_{1}}\cdots f_{n}^{w_{n}}}$ logaritmik dışbükeydir.
• ${\displaystyle \{f_{i}\}_{i\in I}}$ logaritmik dışbükeylerden oluşan bir aile ise, o zaman, ${\displaystyle g=\sup _{i\in I}f_{i}}$ logaritmik dışbükeydir.
• ${\displaystyle f\colon X\to I\subseteq \mathbf {R} }$ dışbükeyse ve ${\displaystyle g\colon I\to \mathbf {R} _{\geq 0}}$ logaritmik dışbükey ve azalmayan bir fonksiyonsa, o zaman ${\displaystyle g\circ f}$ logaritmik dışbükeydir.

Özellikler

Logaritmik dışbükey bir fonksiyon ${\displaystyle f}$, artan dışbükey fonksiyon ${\displaystyle e^{x}}$ ile tanım gereği dışbükey olan ${\displaystyle \log \circ f}$ fonksiyonun bileşkesi olduğundan dışbükey bir fonksiyon olur. Ancak, tersi durum her zaman geçerli değildir ve logaritmik dışbükeylik olağan dışbükeylikten daha kesin ve güçlü bir özelliktir. Örneğin, ${\displaystyle f(x)=x^{2}}$ dışbükeydir ama ${\displaystyle \log f(x)=2\log |x|}$ dışbükey değildir.

Örnekler

• ${\displaystyle f(x)=\exp(|x|^{p})}$ fonksiyonu ${\displaystyle p\geq 1}$ iken logaritmik dışbükeydir ve ${\displaystyle p>1}$ iken kesin logaritmik dışbükeydir.
• ${\displaystyle f(x)={\frac {1}{x^{p}}}}$ fonksiyonu ${\displaystyle (0,\infty )}$ üzerinde bütün ${\displaystyle p>0}$ için kesin logaritmik dışbükeydir.
• Euler gama fonksiyonu pozitif gerçel sayılar üzerine kısıtlandığında kesin logaritmik dışbükeydir. Aslında, bu özellik, Bohr-Mollerup teoremi ile Euler gama fonksiyonunu karakterize etmek için kullanılan şartlardan biridir.

Ayrıca bakınız

Notlar

1. ^ TÜBA Akademik Bilim Terimleri Sözlüğü'nde logaritmik dışbükey fonksiyon sayfası
2. ^ Montel 1928.
3. ^ NiculescuPersson 2006, s. 70.

Kaynakça

1. ^ Kingman, J.F.C. 1961. A convexity property of positive matrices. Quart. J. Math. Oxford (2) 12,283-284.