Bu madde, uygun değildir. (Aralık 2019) |
Lorentz faktörü veya Lorentz terimi bir cismin herhangi bir hıza sahip olmadığı durumla bir hıza sahip olması sırasında kütle, zaman ve uzay ölçümlerinde oluşacak ölçüm farklılıklarını açıklayan niceliktir. Lorentz faktörü, referans çerçeveleri arasında dönüşüm yapılabilmesini sağlayan Lorentz dönüşümünden doğar. Faktör, içindeki erken görünümü yüzünden Hollandalı fizikçi Hendrik Lorentz adına ithaf edilmiştir.
Lorentz faktörünün aynı anda her yerde bulunması nedeniyle, genel olarak γ (Yunanca küçük gama) sembolü ile gösterilmiştir. Faktör bazen (özellikle Işıktan hızlı hareketin tartışmasında) γ yerine daha çok Γ (Yunanca büyük-gama) olarak yazılır.
Tanım
Lorentz faktörü matematiksel olarak şöyle tanımlanır:
burada:
- v bağıl hızdır,
- c Işığın vakumda sahip olduğu hızdır (ışık hızı).
- β v'nin c'ye bölümüdür.
- t zaman koordinatıdır.
- τ bir gözlemcinin kendi referans sisteminde gözlemlediği zaman aralığıdır. (en:)
Bu, tanımlamanın sadece bir yolu olsa da, uygulamada en çok kullanılan formudur. Tanımın alternatif formları için aşağıya bakınız.
Tanımı tamamlamak için, bazı yazarlar şöyle tanımlar:
bakınız ().
Lorentz faktörünün kullanımı
Aşağıda özel görelilikte Lorentz faktörünün γ olarak kullanıldığı bazı formüller gösterilmiştir:
- Lorentz dönüşümü: En basit durumda x-ekseninde referans çerçeveleri arasında düzgün doğrusal hareket (v) olduğunda bir eylemsiz referans çerçevesinden (x, y, z, t) diğer eylemsiz referans çerçevesine (x′, y′, z′, t′) göre uzayzaman koordinatlarının nasıl değiştiğini açıklar. X-ekseni dışındaki eksenler burada gösterilmemiştir.
Yukarıdaki dönüşümlerin sonuçları şunlardır:
- Zaman genişlemesi: Hareket eden referans çerçevesindeki birim zaman (∆t′) hareket etmeyen referans çerçevesindeki birim zamandan (∆t) daha uzundur:
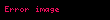
- : Bir cismin eylemsiz referans çerçevesine göre düzgün doğrusal hareket yaparken sahip olduğu birim uzunluk (∆x′) cismin eylemsiz referans çerçevesine göre hareketsiz olduğu zamanki birim uzunluğundan (∆x), kısadır. Cismin kendi durağan referans çerçevesinde de birim uzunluk ∆x olacağından hızlanan cisimlerin hız doğrultusunda kısalacağı söylenebilir.
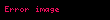
Momentum ve enerjinin korunumu şu sonuçlara yol açar:
- Göreli kütle: Cismin eylemsiz referans çerçevesine göre düzgün doğrusal hareket yaparsa sahip olacağı kütle m cismin durgun kütlesi m0'dan büyüktür:
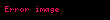
- (Göreli momentum): Göreli momentum ilişkisi klasik momentumla aynı formu alır fakat klasik kütle yeni göreli kütle kullanır:
- : Göreli kinetik enerji cismin hareket halindeyken sahip olduğu toplam enerjiden cisim hareketsizken sahip olduğu toplam enerjinin çıkartılmasına eşittir.
Lorentz faktörü (
Sayısal değerler

Aşağıdaki tabloda sol sütunda β, orta sütunda Lorentz faktörü, son sütunda Lorentz faktörünün tersi gösterilmiştir.
| Hız (c'türünden) | Lorentz faktörü | Tersi |
|---|---|---|
 |  |  |
| 0.000 | 1.000 | 1.000 |
| 0.100 | 1.005 | 0.995 |
| 0.200 | 1.021 | 0.980 |
| 0.300 | 1.048 | 0.954 |
| 0.400 | 1.091 | 0.917 |
| 0.500 | 1.155 | 0.866 |
| 0.600 | 1.250 | 0.800 |
| 0.700 | 1.400 | 0.714 |
| 0.800 | 1.667 | 0.600 |
| 0.866 | 2.000 | 0.500 |
| 0.900 | 2.294 | 0.436 |
| 0.990 | 7.089 | 0.141 |
| 0.999 | 22.366 | 0.045 |
Lorentz faktörünün alternatif temsilleri
Lorentz faktörünü yazmak için başka yollar da vardır. Yukarıda v hızı kullanıldı ama hız gibi momentum ve β de tanımlamak için uygundur.
Momentum
Göreli momentum formülünü Lorentz faktörü için çözmek şu formüle yol açar:
Bu forma çok sık rastlanılmaz fakat bu formu kullanır.
Hız oranı
Hız oranının (
Ayrıca γ ((hiperbolik özdeşliklerin)) kullanımı ile şuna yol açar:
Seri açılımı (hız)
Lorenz faktörünün bir Maclaurin serisi vardır:
Lorentz faktörünü γ ≈ 1 + 1/2β2 olarak almak düşük hızlarda göreli etkileri hesaplamak için kullanılabilir. v < 0.4 c (v < 120,000 km/s) için %1 hata payı ve v < 0.22 c (v < 66,000 km/s) için de %0.1 hata payı anlamına gelir.
Bu dizinin kısaltılmış versiyonları fizikçilerin özel göreliliğin düşük hızlarda klasik mekaniğe indirgendiğinin kanıtlamasını sağlar. Özel göreliliğin, aşağıdaki iki denklemi düşünülsün:
γ ≈ 1 ve γ ≈ 1 + 1/2β2, için sırasıyla, bu onların klasik mekanikteki eşdeğerine indirger:
Lorentz faktörü denklemi ayrıca şu şekilde tekrar yazılabilir:
Lorentz faktörü denkleminin şu hali asimptotik bir biçime sahiptir:
İlk iki terim zaman zaman büyük hızlı γ değerlerden hızları hesaplamak için kullanılır.
Ayrıca bakınız
Kaynakça
- ^ One universe 1 Kasım 2004 tarihinde Wayback Machine sitesinde ., by Neil deGrasse Tyson, Charles Tsun-Chu Liu, and Robert Irion.
- ^ a b Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009,
- ^ Yaakov Friedman, Physical Applications of Homogeneous Balls, Progress in Mathematical Physics 40 Birkhäuser, Boston, 2004, pages 1-21.
- ^ Young; Freedman (2008). Sears' and Zemansky's University Physics (12.12yayıncı=Pearson Ed. & Addison-Wesley bas.). ISBN .
- ^ Synge, J.L (1957). The Relativistic Gas. Series in physics. North-Holland. LCCN 57-003567
- ^ Kinematics 21 Kasım 2014 tarihinde Wayback Machine sitesinde ., by , See page 7 for definition of rapidity.
Dış bağlantılar
- Merrifield, Michael. "γ – Lorentz Factor (and time dilation)". Sixty Symbols. for the University of Nottingham. 7 Şubat 2016 tarihinde kaynağından . Erişim tarihi: 18 Kasım 2013.
- Merrifield, Michael. "γ2 – Gamma Reloaded". Sixty Symbols. for the University of Nottingham. 7 Şubat 2016 tarihinde kaynağından . Erişim tarihi: 18 Kasım 2013.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Aralik 2019 Lorentz faktoru veya Lorentz terimi bir cismin herhangi bir hiza sahip olmadigi durumla bir hiza sahip olmasi sirasinda kutle zaman ve uzay olcumlerinde olusacak olcum farkliliklarini aciklayan niceliktir Lorentz faktoru referans cerceveleri arasinda donusum yapilabilmesini saglayan Lorentz donusumunden dogar Faktor icindeki erken gorunumu yuzunden Hollandali fizikci Hendrik Lorentz adina ithaf edilmistir Lorentz faktorunun ayni anda her yerde bulunmasi nedeniyle genel olarak g Yunanca kucuk gama sembolu ile gosterilmistir Faktor bazen ozellikle Isiktan hizli hareketin tartismasinda g yerine daha cok G Yunanca buyuk gama olarak yazilir TanimLorentz faktoru matematiksel olarak soyle tanimlanir g 11 v2 c2 11 b2 dtdt displaystyle gamma frac 1 sqrt 1 v 2 c 2 frac 1 sqrt 1 beta 2 frac mathrm d t mathrm d tau burada v bagil hizdir c Isigin vakumda sahip oldugu hizdir isik hizi b v nin c ye bolumudur t zaman koordinatidir t bir gozlemcinin kendi referans sisteminde gozlemledigi zaman araligidir en Bu tanimlamanin sadece bir yolu olsa da uygulamada en cok kullanilan formudur Tanimin alternatif formlari icin asagiya bakiniz Tanimi tamamlamak icin bazi yazarlar soyle tanimlar a 1g 1 v2 c2 displaystyle alpha frac 1 gamma sqrt 1 v 2 c 2 bakiniz Lorentz faktorunun kullanimiAsagida ozel gorelilikte Lorentz faktorunun g olarak kullanildigi bazi formuller gosterilmistir Lorentz donusumu En basit durumda x ekseninde referans cerceveleri arasinda duzgun dogrusal hareket v oldugunda bir eylemsiz referans cercevesinden x y z t diger eylemsiz referans cercevesine x y z t gore uzayzaman koordinatlarinin nasil degistigini aciklar X ekseni disindaki eksenler burada gosterilmemistir t g t vxc2 displaystyle t gamma left t frac vx c 2 right x g x vt displaystyle x gamma left x vt right Yukaridaki donusumlerin sonuclari sunlardir Zaman genislemesi Hareket eden referans cercevesindeki birim zaman t hareket etmeyen referans cercevesindeki birim zamandan t daha uzundur Dt gDt displaystyle Delta t gamma Delta t Bir cismin eylemsiz referans cercevesine gore duzgun dogrusal hareket yaparken sahip oldugu birim uzunluk x cismin eylemsiz referans cercevesine gore hareketsiz oldugu zamanki birim uzunlugundan x kisadir Cismin kendi duragan referans cercevesinde de birim uzunluk x olacagindan hizlanan cisimlerin hiz dogrultusunda kisalacagi soylenebilir Dx Dx g displaystyle Delta x Delta x gamma Momentum ve enerjinin korunumu su sonuclara yol acar Goreli kutle Cismin eylemsiz referans cercevesine gore duzgun dogrusal hareket yaparsa sahip olacagi kutle m cismin durgun kutlesi m0 dan buyuktur m gm0 displaystyle m gamma m 0 Goreli momentum Goreli momentum iliskisi klasik momentumla ayni formu alir fakat klasik kutle yeni goreli kutle kullanir p mv gm0v displaystyle vec p m vec v gamma m 0 vec v Goreli kinetik enerji cismin hareket halindeyken sahip oldugu toplam enerjiden cisim hareketsizken sahip oldugu toplam enerjinin cikartilmasina esittir Ek E E0 g 1 m0c2 displaystyle E k E E 0 gamma 1 m 0 c 2 Lorentz faktoru g displaystyle gamma vc displaystyle tfrac v c nin bir fonksiyonu oldugundan goreli olmayan limit limv c 0Ek 12m0v2 textstyle lim v c to 0 E k tfrac 1 2 m 0 v 2 olarak bulunur Bu kinetik enerjinin klasik mekanikteki halidir Sayisal degerlerHizin bir fonksiyonu olarak Lorentz faktorunun grafigi Lorentz faktorunun baslangic degeri 1 v 0 oldugunda olur Hiz isik hizina yaklastikca v c Lorentz faktoru sinirsiz olarak artar g Asagidaki tabloda sol sutunda b orta sutunda Lorentz faktoru son sutunda Lorentz faktorunun tersi gosterilmistir Hiz c turunden Lorentz faktoru Tersib v c displaystyle beta v c g displaystyle gamma 1 g displaystyle 1 gamma 0 000 1 000 1 0000 100 1 005 0 9950 200 1 021 0 9800 300 1 048 0 9540 400 1 091 0 9170 500 1 155 0 8660 600 1 250 0 8000 700 1 400 0 7140 800 1 667 0 6000 866 2 000 0 5000 900 2 294 0 4360 990 7 089 0 1410 999 22 366 0 045Lorentz faktorunun alternatif temsilleriLorentz faktorunu yazmak icin baska yollar da vardir Yukarida v hizi kullanildi ama hiz gibi momentum ve b de tanimlamak icin uygundur Momentum Goreli momentum formulunu Lorentz faktoru icin cozmek su formule yol acar g 1 pm0c 2 displaystyle gamma sqrt 1 left frac p m 0 c right 2 Bu forma cok sik rastlanilmaz fakat bu formu kullanir Hiz orani Hiz oraninin vc displaystyle tfrac v c taniminin Hiperbolik aci f ile yapilmasi tanh f b displaystyle tanh varphi beta Ayrica g hiperbolik ozdesliklerin kullanimi ile suna yol acar g cosh f 11 tanh2 f 11 b2 displaystyle gamma cosh varphi frac 1 sqrt 1 tanh 2 varphi frac 1 sqrt 1 beta 2 Seri acilimi hiz Lorenz faktorunun bir Maclaurin serisi vardir g 11 b2 n 0 b2n k 1n 2k 12k 1 12b2 38b4 516b6 35128b8 displaystyle begin aligned gamma amp dfrac 1 sqrt 1 beta 2 amp sum n 0 infty beta 2n prod k 1 n left dfrac 2k 1 2k right amp 1 frac 1 2 beta 2 frac 3 8 beta 4 frac 5 16 beta 6 frac 35 128 beta 8 cdots end aligned Lorentz faktorunu g 1 1 2b2 olarak almak dusuk hizlarda goreli etkileri hesaplamak icin kullanilabilir v lt 0 4 c v lt 120 000 km s icin 1 hata payi ve v lt 0 22 c v lt 66 000 km s icin de 0 1 hata payi anlamina gelir Bu dizinin kisaltilmis versiyonlari fizikcilerin ozel goreliligin dusuk hizlarda klasik mekanige indirgendiginin kanitlamasini saglar Ozel goreliligin asagidaki iki denklemi dusunulsun p gmv displaystyle vec p gamma m vec v E gmc2 displaystyle E gamma mc 2 g 1 ve g 1 1 2b2 icin sirasiyla bu onlarin klasik mekanikteki esdegerine indirger p mv displaystyle vec p m vec v E mc2 12mv2 displaystyle E mc 2 frac 1 2 mv 2 Lorentz faktoru denklemi ayrica su sekilde tekrar yazilabilir b 1 1g2 displaystyle beta sqrt 1 frac 1 gamma 2 Lorentz faktoru denkleminin su hali asimptotik bir bicime sahiptir b 1 12g 2 18g 4 116g 6 5128g 8 displaystyle beta 1 frac 1 2 gamma 2 frac 1 8 gamma 4 frac 1 16 gamma 6 frac 5 128 gamma 8 cdots Ilk iki terim zaman zaman buyuk hizli g degerlerden hizlari hesaplamak icin kullanilir Ayrica bakinizEylemsiz referans cercevesi Lorentz donusumuKaynakca One universe 1 Kasim 2004 tarihinde Wayback Machine sitesinde by Neil deGrasse Tyson Charles Tsun Chu Liu and Robert Irion a b Dynamics and Relativity J R Forshaw A G Smith Wiley 2009 ISBN 978 0 470 01460 8 Yaakov Friedman Physical Applications of Homogeneous Balls Progress in Mathematical Physics 40 Birkhauser Boston 2004 pages 1 21 Young Freedman 2008 Sears and Zemansky s University Physics 12 12yayinci Pearson Ed amp Addison Wesley bas ISBN 978 0 321 50130 1 Synge J L 1957 The Relativistic Gas Series in physics North Holland LCCN 57 003567 Kinematics 21 Kasim 2014 tarihinde Wayback Machine sitesinde by See page 7 for definition of rapidity Dis baglantilarMerrifield Michael g Lorentz Factor and time dilation Sixty Symbols for the University of Nottingham 7 Subat 2016 tarihinde kaynagindan Erisim tarihi 18 Kasim 2013 Merrifield Michael g2 Gamma Reloaded Sixty Symbols for the University of Nottingham 7 Subat 2016 tarihinde kaynagindan Erisim tarihi 18 Kasim 2013
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State