Hız bir nesnenin hareket yönü ile birlikte olan süratini ifade eder. Hız, cisimlerin hareketini tanımlayan bir klasik mekanik dalı olan kinematikte temel bir kavramdır.
Hız | |
 | |
Yarış arabaları kıvrımlı pist üzerinde manevra yaptıklarında yön değiştirmekte oldukları için, süratleri sabit kalmakla birlikte, vektörel hızları değişkenlik gösterir. | |
| Yaygın sembol(ler): | v, v, v→, v |
| temel SI birimlerinden türetimi: | L T−1 |
| SI birimi: | m/s |
Hız, hem büyüklük hem de yön içeren fiziksel bir vektör niceliğidir. Hızın skaler mutlak değeri sürat olarak isimlendirilir ve bu, niceliği SI (metrik sistem) kapsamında metre bölü saniye (m/s veya m⋅s−1) birimleri ile ölçülen tutarlı bir türetilmiş birimdir. Örneğin, "saniyede 5 metre" bir skaler değer iken, "saniyede 5 metre doğuya" bir vektör olarak tanımlanır. Sürat, yön veya her ikisinin değişmesi durumunda, ilgili nesnenin ivmelenme süreci içinde olduğu ifade edilir.
Tanım
Ortalama hız
Bir nesnenin belirlenen bir zaman aralığındaki ortalama hızı, bu süre zarfında mekansal konumundaki değişim olan 
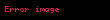

Anlık hız

Bir cismin anlık hızı, zaman diliminin sıfıra yaklaşması durumunda elde edilen ortalama hızın limiti olarak tanımlanır. Belirli bir t zamanında, zamanla ilgili olarak cismin konumunun türevi alınarak hesaplanabilir:

Bu türev denkleminin analizinden, tek boyutlu bir örnekte, hız-zaman grafiği (v'ye karşı t grafiği) altında kalan alanın, yer değiştirme, s'yi ifade ettiği sonucuna varılabilir. Matematiksel analiz çerçevesinde, hız fonksiyonunun v(t) integrali, yer değiştirme fonksiyonu s(t) olarak ifade edilir. Bu, şekilde gösterilen eğrinin altındaki sarı alanla örtüşmektedir.
Anlık hız kavramı ilk bakışta sezgiye aykırı gibi algılanabilir; ancak, bu, nesnenin o anda ivmelenmeyi durdurduğu takdirde seyahat etmeye devam edeceği hız olarak düşünülebilir.
Sürat ile hız arasındaki farklar

Bir nesnenin hareket hızını ifade etmek amacıyla günlük konuşmalarda sürat ve hız terimleri yer değiştirilerek kullanılmakta olup, bilimsel anlamda bu iki kavram arasında belirgin farklar bulunmaktadır. Sürat, bir hız vektörünün skaler büyüklüğü olarak tanımlanır ve yalnızca nesnenin ne kadar hızlı hareket ettiğini belirtir. Öte yandan hız, nesnenin hem süratini hem de hareket yönünü içerir.
Bir nesnenin sabit hız ile hareket edebilmesi için, sürekli olarak sabit bir sürat ile ve değişmeyen bir yönde ilerlemesi gerekmektedir. Sabit yönelim, nesnenin düz bir gidişizi boyunca hareketini sınırlar; bu durum, sabit bir süratle düz bir hat üzerinde ilerlemeyi gerektirir.
Örneğin, dairesel bir parkurda sürekli olarak saatte 20 kilometre süratle ilerleyen bir otomobil, sabit bir sürate sahiptir ancak yönünün sürekli değişiyor olması sebebiyle sabit bir hıza sahip değildir. Bu yüzden, aracın bir ivmelenme içerisinde olduğu düşünülmektedir.
Birimler
Zamana göre konumun türevi alındığında, mekansal değişim (metre) ile zaman aralığındaki değişim (saniye) oranı hesaplandığından, hızın birimi olarak metre/saniye (m/s) kullanılır.
Hareket denklemleri
Ortalama hız
Hız, pozisyonun zamanla nasıl değiştiğinin bir oranı olarak ifade edilir ve bu durum bazen anlık hız terimi ile daha da belirginleştirilir. Belirli uygulamalarda, bir nesnenin değişken hızla aynı zaman diliminde elde edeceği yer değiştirmeye eşdeğer sabit bir hızın belirlenmesi gerekebilir. Bu, v(t) üzerinden belirli bir Δt zaman periyodu için geçerlidir. Ortalama hız, aşağıdaki formülle hesaplanabilir:
Ortalama hız, bir nesnenin ortalama süratinden her zaman daha az veya ona eşit olur. Bu, mesafe her zaman kesinlikle artarken, yer değiştirme büyüklüğünün artabileceği veya azalabileceği ve yön değiştirebileceği gerçeği göz önüne alındığında anlaşılabilir.
Yer değiştirme-zaman (x karşısında t) grafiği bağlamında, herhangi bir noktadaki eğriye teğet çizginin eğimi olarak anlık hız (veya daha sade bir ifade ile hız) kabul edilirken, iki nokta arasındaki kiriş çizgisinin eğimi, ortalama hız için zaman diliminin sınırlarına karşılık gelen t koordinatları ile hesaplanan ortalama hızı ifade eder.
Özel durumlar
- Bir parçacık farklı zaman dilimlerinde farklı sabit süratlerle v1, v2, v3, ..., vn ilerlediğinde, yolculuğun toplam süresi boyunca hesaplanan ortalama sürat, aşağıdaki formül ile verilir:
Eğer t1 = t2 = t3 = ... = t durumunda ise, hızların aritmetik ortalamasına dayanarak ortalama sürat aşağıdaki gibi hesaplanır

- Çeşitli mesafeler s1, s2, s3, ..., sn farklı süratlerle v1, v2, v3, ..., vn ile kat edildiğinde, parçacığın toplam mesafedeki ortalama sürati aşağıdaki formülle belirlenir


İvmelenme ile olan bağlantısı
Hız, bir cismin konumundaki değişim oranı olarak ifade edilirken, çoğu zaman bir nesnenin ivmelenmesine ilişkin bir ifade ile başlanması alışılagelmiştir. Şekildeki üç yeşil teğet çizgiden görülebileceği gibi, bir nesnenin belirli bir anda gösterdiği anlık ivmelenme, bu noktada v(t) grafiğinin eğrisine çizilen teğetin eğimi olarak değerlendirilir. Başka bir ifadeyle, anlık ivmelenme, hızın zaman cinsinden türevi olarak tanımlanmaktadır:
Bu noktadan itibaren, zaman grafiği ile karşılaştırıldığında a(t) ivmesinin temsil ettiği alanı dikkate alarak hızın bir ifadesini türetebiliriz. Önceden de ifade edildiği üzere, bu süreç integral kavramının uygulanmasıyla gerçekleştirilir:

Sabit ivmelenme
Sabit ivmelenme durumunda, hızın analizi, hareket denklemleri aracılığıyla yapılabilir. a vektörünün sabit bir değer olarak ele alınması durumunda, aşağıdaki ifadenin kolaylıkla kanıtlanabileceği görülür:


Zamandan bağımsız olarak hızın bir ifadesinin türetilmesi mümkündür; bu ifadeye Torricelli denklemi adı verilir ve aşağıdaki gibi formüle edilir:



İlgili denklemler, hem Newton mekaniği hem de özel görelilik bağlamında uygulanabilir. Bu iki kuram arasındaki temel ayrım, farklı gözlemcilerin aynı durumu nasıl değerlendirdikleri ile ilgilidir. Newton mekaniğine göre, tüm gözlemciler zaman (t) değeri konusunda hemfikirdir ve konumun dönüşüm kuralları, ivmelenmeyen her gözlemcinin bir cismin ivmelenmesini aynı değerlerle tanımlamasını sağlar; bu durum özel görelilikte mümkün değildir. Yani, özel görelilikte, yalnızca göreceli hızlar hesaplanabilir.
Hıza bağlı nicelikler
Momentum
Klasik mekanikte, Newton'un ikinci kanunu momentumu, p, bir nesnenin kütlesi ile hızının vektörel çarpımı olarak tanımlar; bu ilişki matematiksel olarak
formülüyle ifade edilir, burada m cismin kütlesini temsil eder.Kinetik enerji
Bir nesnenin hareket durumundaki kinetik enerjisi, onun hızına göre değişkenlik göstermektedir ve bu enerji, kinetik enerjiyi belirleyen şu formülle hesaplanır
burada Ek, kinetik enerji miktarını temsil etmektedir. Kinetik enerji, hızın karesi ile orantılı olduğundan dolayı bir skaler büyüklüktür.Akışkan direnci (Sürtünme)
Akışkanlar dinamiği alanında, bir nesnenin çevresindeki akışkanla ilişkili hareketine zıt yönde etki eden kuvvete denir. Sürtünme kuvveti, 

, akışkanın yoğunluk değerini temsil eder,
, nesnenin akışkana göre göreli süratini,
, nesnenin kesit alanını,
, gösterir – bu, boyutsuz bir sayıdır.
Kaçış hızı
Kaçış hızı, bir nesnenin, Dünya gibi büyük bir kütleye sahip bir cisimden kaçışını sağlayacak minimum sürati ifade eder. Bu sürat, nesnenin yerçekimsel potansiyel enerjisi (daima negatif değer alır) ile birleştiğinde toplam enerjinin sıfır olmasını sağlayan kinetik enerjiyi yansıtır. Bir gezegenin merkezinden r uzaklıkta bir cismin kaçış süratini belirleyen genel formül şöyledir:

Özel görelilikteki Lorentz faktörü
Özel görelilik alanında, boyutsuz olarak tanımlanan Lorentz faktörü sıklıkla önem arz eder ve aşağıdaki formülle ifade edilir
Bu denklemde, γ, Lorentz faktörünü ve c, ışık hızını temsil eder. Bu faktör, nesnelerin ışık hızına yaklaştıkça nasıl davrandığını matematiksel olarak modellemek için kullanılır.
Bağıl hız
Bağıl hız (göreceli hız), iki nesne arasındaki hızın, tek bir koordinat sistemi çerçevesinde değerlendirilmesi ile elde edilen bir ölçümdür. Bu kavram, hem klasik hem de modern fizikte merkezi bir öneme sahiptir; zira birçok fiziksel sistem, birden fazla parçacığın birbirlerine göre hareketini incelemektedir.
Örneğin, A cisminin v vektörü ile ve B cisminin w hız vektörü ile hareket ettiği düşünüldüğünde; bu mutlak hızlar genellikle aynı eylemsiz referans çerçevesinde tanımlanır. Bu durumda, A cisminin B cismine göre hızı, iki hız vektörünün farkı olarak şöyle ifade edilir:


Newton mekaniğine göre, göreceli hızın büyüklüğü, seçilen eylemsiz referans çerçevesine bağlı olmaksızın sabit kalır. Ancak, özel görelilik altında bu durum geçerli değildir; özel görelilikte hızlar, tercih edilen referans çerçevesine göre değişiklik gösterir.
Skaler hız değerleri
Tek boyutlu bir durumda, hızlar skaler değerler alır ve ifade edilen denklem şu iki durumdan birini takip eder:


Koordinat sistemleri
Kartezyen koordinatlar
Çok boyutlu Kartezyen koordinat sistemlerinde, hızın her bir bileşeni, sistemdeki boyut eksenleri ile uyumlu şekilde ayrıştırılır. İki boyutlu bir sistemde, x ve y eksenleri mevcut olduğunda, bu eksenlere karşılık gelen hız bileşenleri aşağıdaki gibi ifade edilir:


İki boyutlu hız vektörü, 
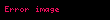
Üç boyutlu sistemlerde eklenen z-ekseni için, ilgili hız bileşeni

Üç boyutlu hız vektörü, 

Farklı ders kitapları, hızın Kartezyen bileşenlerini belirtmek için farklı notasyonlar kullanabilir; örneğin, 





Kutupsal koordinat sistemleri

Kutupsal koordinat sistemlerinde, iki boyutlu bir hızın ifadesi, orijinden uzaklaşan ya da orijine doğru olan hız bileşeni olarak ifade edilen radial hız ve bu hıza dik olan teğetsel hız ile açıklanmaktadır. Bu hız bileşenleri, orijin etrafındaki dönme hızını belirleyen açısal hızdan türetilir; bu sistemde pozitif değerler saat yönünün tersi dönüşü, negatif değerler ise saat yönü dönüşünü gösterir. Bu tür bir açıklama, sağ el koordinat sistemi temel alınarak yapılmıştır.
Radial ve teğetsel hızlar, Kartezyen hız ve yer değiştirme vektörlerinin, bu vektörlerin radial ve teğetsel bileşenlere ayrıştırılmasıyla elde edilir. Teğetsel hız, orijin merkezli bir çember üzerindeki hız bileşenini belirtir.

, teğetsel hızı,
, radial hızı gösterir.
Radial hız (veya radial hızın büyüklüğü), hız vektörü ile radial yöndeki birim vektör arasındaki nokta çarpımı kullanılarak hesaplanır.

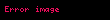 , cismin pozisyonunu ve
, cismin pozisyonunu ve  , radial yönü temsil eder.
, radial yönü temsil eder. Teğetsel hızın (veya teğetsel hızın büyüklüğünün) değeri, radial yönün birim vektörü ile hız vektörünün çapraz çarpım sonucunun büyüklüğü ile belirlenir. Bu değer, hız vektörünün teğetsel yöne göre nokta çarpımı ya da açısal hız 


Açısal momentum, skaler bir ifade olarak, cismin kütlesi ile orijine olan uzaklığının ve bu uzaklık boyunca cismin teğetsel hızının çarpımı şeklinde tanımlanır. Alternatif olarak, kütlenin, uzaklığın karesi ile açısal hızın çarpımı olarak da ifade edilir. Açısal momentum için kullanılan işaret kuralı, açısal hız için belirlenen kuralla aynıdır.

kütleyi,
uzaklığın büyüklüğünü temsil eder.
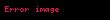
Ayrıca bakınız
- (Görelilik kuramında, Minkowski uzayzamanı için tanımlanmış hızın bir çeşidi)
- Grup hızı (Dalga paketlerinin yayılma hızı)
- (Çok yüksek hızlarda kullanılan terim)
- Faz hızı (Dalga fazlarının yayılma hızı)
- (Görelilikte, yolcu zamanına göre tanımlanan hız)
- (Görelilik hızlarında toplanabilir özellikte bir hız tanımı)
- Terminal hızı (Bir nesnenin serbest düşüşte ulaşabileceği maksimum hız)
- Akış hızı (Bir akışkan içindeki hız vektörlerinin dağılımı)
- (Hızın zamanla nasıl değiştiğini gösteren grafik)
Notlar
- Robert Resnick and Jearl Walker, Fundamentals of Physics, Wiley; 7 Sub edition (June 16, 2004). .
Kaynakça
- ^ "The Feynman Lectures on Physics Vol. I Ch. 8: Motion". www.feynmanlectures.caltech.edu. Erişim tarihi: 5 Ocak 2024.
- ^ David Halliday; Robert Resnick; Jearl Walker (2021). Fundamentals of Physics, Extended (12.12sayfa=71 bas.). John Wiley & Sons. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 71'den alıntı 29 Şubat 2024 tarihinde Wayback Machine sitesinde .
- ^ Richard P. Olenick; Tom M. Apostol; David L. Goodstein (2008). The Mechanical Universe: Introduction to Mechanics and Heat (illustrated, reprinted bas.). Cambridge University Press. s. 84. ISBN . 3 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 84'ten alıntı 6 Kasım 2023 tarihinde Wayback Machine sitesinde .
- ^ Michael J. Cardamone (2007). Fundamental Concepts of Physics. Universal-Publishers. s. 5. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 5'ten alıntı 2 Kasım 2023 tarihinde Wayback Machine sitesinde .
- ^ Jerry D. Wilson; Anthony J. Buffa; Bo Lou (2022). College Physics Essentials, Eighth Edition (Two-Volume Set) (illustrated bas.). CRC Press. s. 40. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 40'tan alıntı 2 Kasım 2023 tarihinde Wayback Machine sitesinde .
- ^ David Halliday; Robert Resnick; Jearl Walker (2021). Fundamentals of Physics, Extended (12.12yayıncı=John Wiley & Sons bas.). s. 70. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 70'den alıntı 27 Ekim 2023 tarihinde Wayback Machine sitesinde .
- ^ Adrian Banner (2007). The Calculus Lifesaver: All the Tools You Need to Excel at Calculus (illustrated bas.). Princeton University Press. s. 350. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 350'den alıntı 29 Şubat 2024 tarihinde Wayback Machine sitesinde .
- ^ a b Giri & Bannerjee (2002). Statistical Tools and Technique. Academic Publishers. s. 4. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 4'ten alıntı 29 Şubat 2024 tarihinde Wayback Machine sitesinde .
- ^ Bekir Karaoglu (2020). Classical Physics: A Two-Semester Coursebook. Springer Nature. s. 41. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 41'den alıntı 2 Kasım 2023 tarihinde Wayback Machine sitesinde .
- ^ David Halliday; Robert Resnick; Jearl Walker (2010). Fundamentals of Physics, Chapters 33-37. John Wiley & Sons. s. 1080. ISBN . 27 Ekim 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 1080'den alıntı 2 Kasım 2023 tarihinde Wayback Machine sitesinde .
- ^ Dünya'nın atmosferi için, hava yoğunluğu kullanılarak hesaplanır ve 0 °C ile 1 atmosfer altında 1.293 kg/m3 değerindedir.
- ^ Jim Breithaupt (2000). New Understanding Physics for Advanced Level (illustrated bas.). Nelson Thornes. s. 231. ISBN . 29 Şubat 2024 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 231'den alıntı 2 Kasım 2023 tarihinde Wayback Machine sitesinde .
- ^ Eckehard W Mielke (2022). Modern Aspects Of Relativity. World Scientific. s. 98. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 98'den alıntı 2 Mart 2024 tarihinde Wayback Machine sitesinde .
- ^ . 26 Kasım 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Nisan 2024.
- ^ "The Feynman Lectures on Physics Vol. I Ch. 9: Newton's Laws of Dynamics". www.feynmanlectures.caltech.edu. Erişim tarihi: 4 Ocak 2024.
- ^ White, F. M. (2008). Fluid mechanics. The McGraw Hill Companies,.
- ^ E. Graham; Aidan Burrows; Brian Gaulter (2002). Mechanics, Volume 6 (illustrated bas.). Heinemann. s. 77. ISBN . 2 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 77'den alıntı 2 Kasım 2023 tarihinde Wayback Machine sitesinde .
- ^ Anup Goel; H. J. Sawant (2021). Engineering Mechanics. Technical Publications. s. 8. ISBN . 27 Ekim 2023 tarihinde kaynağından . Erişim tarihi: 16 Nisan 2024. Sayfa 8'den alıntı 2 Kasım 2023 tarihinde Wayback Machine sitesinde .
Dış bağlantılar
| Wikimedia Commons'ta Velocity ile ilgili ortam dosyaları bulunmaktadır. |
- Velocity and Acceleration
- Introduction to Mechanisms (Carnegie Mellon University)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Hiz bir nesnenin hareket yonu ile birlikte olan suratini ifade eder Hiz cisimlerin hareketini tanimlayan bir klasik mekanik dali olan kinematikte temel bir kavramdir HizYaris arabalari kivrimli pist uzerinde manevra yaptiklarinda yon degistirmekte olduklari icin suratleri sabit kalmakla birlikte vektorel hizlari degiskenlik gosterir Yaygin sembol ler v v v vtemel SI birimlerinden turetimi L T 1SI birimi m s Hiz hem buyukluk hem de yon iceren fiziksel bir vektor niceligidir Hizin skaler mutlak degeri surat olarak isimlendirilir ve bu niceligi SI metrik sistem kapsaminda metre bolu saniye m s veya m s 1 birimleri ile olculen tutarli bir turetilmis birimdir Ornegin saniyede 5 metre bir skaler deger iken saniyede 5 metre doguya bir vektor olarak tanimlanir Surat yon veya her ikisinin degismesi durumunda ilgili nesnenin ivmelenme sureci icinde oldugu ifade edilir TanimOrtalama hiz Bir nesnenin belirlenen bir zaman araligindaki ortalama hizi bu sure zarfinda mekansal konumundaki degisim olan Ds displaystyle Delta s degeri ilgili zaman araliginin suresi Dt displaystyle Delta t ile bolundugunde elde edilen degerdir Bu iliski matematiksel olarakv DsDt displaystyle bar v frac Delta s Delta t seklinde ifade edilmektedir Anlik hiz Hiz zaman grafigi ornegi y ekseni uzerindeki hiz v ivme a egrinin farkli noktalarinda ivme degerlerini temsil eden uc yesil teget cizgisi ve yer degistirme s egrinin altindaki sari alan Bir cismin anlik hizi zaman diliminin sifira yaklasmasi durumunda elde edilen ortalama hizin limiti olarak tanimlanir Belirli bir t zamaninda zamanla ilgili olarak cismin konumunun turevi alinarak hesaplanabilir v limDt 0DsDt dsdt displaystyle boldsymbol v lim Delta t to 0 frac Delta boldsymbol s Delta t frac d boldsymbol s dt Bu turev denkleminin analizinden tek boyutlu bir ornekte hiz zaman grafigi v ye karsi t grafigi altinda kalan alanin yer degistirme s yi ifade ettigi sonucuna varilabilir Matematiksel analiz cercevesinde hiz fonksiyonunun v t integrali yer degistirme fonksiyonu s t olarak ifade edilir Bu sekilde gosterilen egrinin altindaki sari alanla ortusmektedir Anlik hiz kavrami ilk bakista sezgiye aykiri gibi algilanabilir ancak bu nesnenin o anda ivmelenmeyi durdurdugu takdirde seyahat etmeye devam edecegi hiz olarak dusunulebilir Surat ile hiz arasindaki farklar Klasik bir parcacigin kinematik ozellikleri kutle m konum r hiz v ivme a Bir nesnenin hareket hizini ifade etmek amaciyla gunluk konusmalarda surat ve hiz terimleri yer degistirilerek kullanilmakta olup bilimsel anlamda bu iki kavram arasinda belirgin farklar bulunmaktadir Surat bir hiz vektorunun skaler buyuklugu olarak tanimlanir ve yalnizca nesnenin ne kadar hizli hareket ettigini belirtir Ote yandan hiz nesnenin hem suratini hem de hareket yonunu icerir Bir nesnenin sabit hiz ile hareket edebilmesi icin surekli olarak sabit bir surat ile ve degismeyen bir yonde ilerlemesi gerekmektedir Sabit yonelim nesnenin duz bir gidisizi boyunca hareketini sinirlar bu durum sabit bir suratle duz bir hat uzerinde ilerlemeyi gerektirir Ornegin dairesel bir parkurda surekli olarak saatte 20 kilometre suratle ilerleyen bir otomobil sabit bir surate sahiptir ancak yonunun surekli degisiyor olmasi sebebiyle sabit bir hiza sahip degildir Bu yuzden aracin bir ivmelenme icerisinde oldugu dusunulmektedir Birimler Zamana gore konumun turevi alindiginda mekansal degisim metre ile zaman araligindaki degisim saniye orani hesaplandigindan hizin birimi olarak metre saniye m s kullanilir Hareket denklemleriOrtalama hiz Hiz pozisyonun zamanla nasil degistiginin bir orani olarak ifade edilir ve bu durum bazen anlik hiz terimi ile daha da belirginlestirilir Belirli uygulamalarda bir nesnenin degisken hizla ayni zaman diliminde elde edecegi yer degistirmeye esdeger sabit bir hizin belirlenmesi gerekebilir Bu v t uzerinden belirli bir Dt zaman periyodu icin gecerlidir Ortalama hiz asagidaki formulle hesaplanabilir Ortalama hiz bir nesnenin ortalama suratinden her zaman daha az veya ona esit olur Bu mesafe her zaman kesinlikle artarken yer degistirme buyuklugunun artabilecegi veya azalabilecegi ve yon degistirebilecegi gercegi goz onune alindiginda anlasilabilir Yer degistirme zaman x karsisinda t grafigi baglaminda herhangi bir noktadaki egriye teget cizginin egimi olarak anlik hiz veya daha sade bir ifade ile hiz kabul edilirken iki nokta arasindaki kiris cizgisinin egimi ortalama hiz icin zaman diliminin sinirlarina karsilik gelen t koordinatlari ile hesaplanan ortalama hizi ifade eder Ozel durumlar Bir parcacik farkli zaman dilimlerinde farkli sabit suratlerle v1 v2 v3 vn ilerlediginde yolculugun toplam suresi boyunca hesaplanan ortalama surat asagidaki formul ile verilir v v1t1 v2t2 v3t3 vntnt1 t2 t3 tn displaystyle bar v v 1 t 1 v 2 t 2 v 3 t 3 dots v n t n over t 1 t 2 t 3 dots t n Eger t1 t2 t3 t durumunda ise hizlarin aritmetik ortalamasina dayanarak ortalama surat asagidaki gibi hesaplanirv v1 v2 v3 vnn 1n i 1nvi displaystyle bar v v 1 v 2 v 3 dots v n over n frac 1 n sum i 1 n v i Cesitli mesafeler s1 s2 s3 sn farkli suratlerle v1 v2 v3 vn ile kat edildiginde parcacigin toplam mesafedeki ortalama surati asagidaki formulle belirlenirv s1 s2 s3 snt1 t2 t3 tn s1 s2 s3 sns1v1 s2v2 s3v3 snvn displaystyle bar v s 1 s 2 s 3 dots s n over t 1 t 2 t 3 dots t n s 1 s 2 s 3 dots s n over s 1 over v 1 s 2 over v 2 s 3 over v 3 dots s n over v n Eger s1 s2 s3 s ise ortalama surat hizlarin harmonik ortalamasina dayali olarak hesaplanirv n 1v1 1v2 1v3 1vn 1 n i 1n1vi 1 displaystyle bar v n left 1 over v 1 1 over v 2 1 over v 3 dots 1 over v n right 1 n left sum i 1 n frac 1 v i right 1 Ivmelenme ile olan baglantisi Hiz bir cismin konumundaki degisim orani olarak ifade edilirken cogu zaman bir nesnenin ivmelenmesine iliskin bir ifade ile baslanmasi alisilagelmistir Sekildeki uc yesil teget cizgiden gorulebilecegi gibi bir nesnenin belirli bir anda gosterdigi anlik ivmelenme bu noktada v t grafiginin egrisine cizilen tegetin egimi olarak degerlendirilir Baska bir ifadeyle anlik ivmelenme hizin zaman cinsinden turevi olarak tanimlanmaktadir Bu noktadan itibaren zaman grafigi ile karsilastirildiginda a t ivmesinin temsil ettigi alani dikkate alarak hizin bir ifadesini turetebiliriz Onceden de ifade edildigi uzere bu surec integral kavraminin uygulanmasiyla gerceklestirilir v a dt displaystyle boldsymbol v int boldsymbol a dt Sabit ivmelenme Sabit ivmelenme durumunda hizin analizi hareket denklemleri araciligiyla yapilabilir a vektorunun sabit bir deger olarak ele alinmasi durumunda asagidaki ifadenin kolaylikla kanitlanabilecegi gorulur v u at displaystyle boldsymbol v boldsymbol u boldsymbol a t burada v zaman t icin hizi u ise zaman t 0 icin baslangic hizini ifade eder Bu denklem hareket formulu x ut at2 2 ile birlestirilerek yer degistirme ile ortalama hiz arasindaki iliski su sekilde formule edilir x u v 2t v t displaystyle boldsymbol x frac boldsymbol u boldsymbol v 2 t boldsymbol bar v t Zamandan bagimsiz olarak hizin bir ifadesinin turetilmesi mumkundur bu ifadeye Torricelli denklemi adi verilir ve asagidaki gibi formule edilir v2 v v u at u at u2 2t a u a2t2 displaystyle v 2 boldsymbol v cdot boldsymbol v boldsymbol u boldsymbol a t cdot boldsymbol u boldsymbol a t u 2 2t boldsymbol a cdot boldsymbol u a 2 t 2 2a x 2a ut 12at2 2t a u a2t2 v2 u2 displaystyle 2 boldsymbol a cdot boldsymbol x 2 boldsymbol a cdot boldsymbol u t tfrac 1 2 boldsymbol a t 2 2t boldsymbol a cdot boldsymbol u a 2 t 2 v 2 u 2 v2 u2 2 a x displaystyle therefore v 2 u 2 2 boldsymbol a cdot boldsymbol x Ilgili denklemler hem Newton mekanigi hem de ozel gorelilik baglaminda uygulanabilir Bu iki kuram arasindaki temel ayrim farkli gozlemcilerin ayni durumu nasil degerlendirdikleri ile ilgilidir Newton mekanigine gore tum gozlemciler zaman t degeri konusunda hemfikirdir ve konumun donusum kurallari ivmelenmeyen her gozlemcinin bir cismin ivmelenmesini ayni degerlerle tanimlamasini saglar bu durum ozel gorelilikte mumkun degildir Yani ozel gorelilikte yalnizca goreceli hizlar hesaplanabilir Hiza bagli niceliklerMomentum Klasik mekanikte Newton un ikinci kanunu momentumu p bir nesnenin kutlesi ile hizinin vektorel carpimi olarak tanimlar bu iliski matematiksel olarak formuluyle ifade edilir burada m cismin kutlesini temsil eder Kinetik enerji Bir nesnenin hareket durumundaki kinetik enerjisi onun hizina gore degiskenlik gostermektedir ve bu enerji kinetik enerjiyi belirleyen su formulle hesaplanirburada Ek kinetik enerji miktarini temsil etmektedir Kinetik enerji hizin karesi ile orantili oldugundan dolayi bir skaler buyukluktur Akiskan direnci Surtunme Akiskanlar dinamigi alaninda bir nesnenin cevresindeki akiskanla iliskili hareketine zit yonde etki eden kuvvete denir Surtunme kuvveti FD displaystyle F D hizin karesi ile orantili olarak ifade edilir ve asagidaki formulle hesaplanir FD 12rv2CDA displaystyle F D tfrac 1 2 rho v 2 C D A Bu formulde r displaystyle rho akiskanin yogunluk degerini temsil eder v displaystyle v nesnenin akiskana gore goreli suratini A displaystyle A nesnenin kesit alanini CD displaystyle C D gosterir bu boyutsuz bir sayidir Kacis hizi Kacis hizi bir nesnenin Dunya gibi buyuk bir kutleye sahip bir cisimden kacisini saglayacak minimum surati ifade eder Bu surat nesnenin yercekimsel potansiyel enerjisi daima negatif deger alir ile birlestiginde toplam enerjinin sifir olmasini saglayan kinetik enerjiyi yansitir Bir gezegenin merkezinden r uzaklikta bir cismin kacis suratini belirleyen genel formul soyledir ve 2GMr 2gr displaystyle v text e sqrt frac 2GM r sqrt 2gr burada G yercekimi sabiti ve g yercekimi ivmesi olarak tanimlanir Dunya nin yuzeyinden hesaplanan kacis surati yaklasik olarak 11 200 m s degerindedir ve bu surat nesnenin hareket yonunden bagimsizdir Bu nedenle kacis hizi terimi teknik olarak yanilticidir kacis surati daha uygun bir ifadedir Atmosferik etkilerden bagimsiz olarak bu suratte hareket eden bir nesne yolunda herhangi bir engel bulunmadigi surece ana govdenin cekim alanindan cikacaktir Ozel gorelilikteki Lorentz faktoru Ozel gorelilik alaninda boyutsuz olarak tanimlanan Lorentz faktoru siklikla onem arz eder ve asagidaki formulle ifade edilir Bu denklemde g Lorentz faktorunu ve c isik hizini temsil eder Bu faktor nesnelerin isik hizina yaklastikca nasil davrandigini matematiksel olarak modellemek icin kullanilir Kosarak hiz alan insanlar Merel de Knegt Silvestercross 2007 Bagil hizBagil hiz goreceli hiz iki nesne arasindaki hizin tek bir koordinat sistemi cercevesinde degerlendirilmesi ile elde edilen bir olcumdur Bu kavram hem klasik hem de modern fizikte merkezi bir oneme sahiptir zira bircok fiziksel sistem birden fazla parcacigin birbirlerine gore hareketini incelemektedir Ornegin A cisminin v vektoru ile ve B cisminin w hiz vektoru ile hareket ettigi dusunuldugunde bu mutlak hizlar genellikle ayni eylemsiz referans cercevesinde tanimlanir Bu durumda A cisminin B cismine gore hizi iki hiz vektorunun farki olarak soyle ifade edilir vAya gore B v w displaystyle boldsymbol v A text ya gore B boldsymbol v boldsymbol w Ayni sekilde B cisminin A cisminin v hizi ile hareketine gore goreceli hizi su sekilde hesaplanir vBye gore A w v displaystyle boldsymbol v B text ye gore A boldsymbol w boldsymbol v Bu hesaplamalarda genellikle iki nesneden bahsi gecen son nesnenin hareketsiz oldugu eylemsiz cerceve tercih edilir Newton mekanigine gore goreceli hizin buyuklugu secilen eylemsiz referans cercevesine bagli olmaksizin sabit kalir Ancak ozel gorelilik altinda bu durum gecerli degildir ozel gorelilikte hizlar tercih edilen referans cercevesine gore degisiklik gosterir Skaler hiz degerleri Tek boyutlu bir durumda hizlar skaler degerler alir ve ifade edilen denklem su iki durumdan birini takip eder vrel v w displaystyle v text rel v w bu ifade iki nesnenin birbirlerine zit yonde hareket ettigi durumlari kapsar ya da vrel v w displaystyle v text rel v w bu ifade ise iki nesnenin ayni yonde hareket ettigi durumlari ifade eder Koordinat sistemleriKartezyen koordinatlar Cok boyutlu Kartezyen koordinat sistemlerinde hizin her bir bileseni sistemdeki boyut eksenleri ile uyumlu sekilde ayristirilir Iki boyutlu bir sistemde x ve y eksenleri mevcut oldugunda bu eksenlere karsilik gelen hiz bilesenleri asagidaki gibi ifade edilir vx dx dt displaystyle v x dx dt bu x eksenindeki degisimi zamana bolerek hesaplanir vy dy dt displaystyle v y dy dt bu ise y eksenindeki degisimi zamana bolerek hesaplanir Bu tanimlar sistemdeki hizin yon ve buyuklugunun anlasilmasina olanak tanir Iki boyutlu hiz vektoru v lt vx vy gt displaystyle textbf v lt v x v y gt biciminde ifade edilir Bu vektorun buyuklugu surati ifade eder ve mesafe formulu kullanilarak hesaplanir v vx2 vy2 displaystyle v sqrt v x 2 v y 2 Uc boyutlu sistemlerde eklenen z ekseni icin ilgili hiz bilesenivz dz dt displaystyle v z dz dt olarak belirlenir Uc boyutlu hiz vektoru v lt vx vy vz gt displaystyle textbf v lt v x v y v z gt seklinde tanimlanmis olup onun buyuklugu de surati yansitir ve su formulle hesaplanir v vx2 vy2 vz2 displaystyle v sqrt v x 2 v y 2 v z 2 Farkli ders kitaplari hizin Kartezyen bilesenlerini belirtmek icin farkli notasyonlar kullanabilir ornegin x displaystyle x y displaystyle y ve z displaystyle z eksenleri icin sirasiyla u displaystyle u v displaystyle v ve w displaystyle w sembolleri tercih edilir Kutupsal koordinat sistemleri Bir gozlemci O nun etrafinda sabit hizla dogrusal hareket eden bir nesnenin cesitli zaman dilimlerinde radial ve tegetsel hiz bilesenlerinin gosterimi Ornegin bir yaya kaldirimda dururken bir aracin duz bir sokaktan gecisi bu duruma ornektir Radial bilesen Doppler etkisi sayesinde algilanabilirken tegetsel bilesen nesnenin konumundaki gorsel degisimlere yol acar Kutupsal koordinat sistemlerinde iki boyutlu bir hizin ifadesi orijinden uzaklasan ya da orijine dogru olan hiz bileseni olarak ifade edilen radial hiz ve bu hiza dik olan tegetsel hiz ile aciklanmaktadir Bu hiz bilesenleri orijin etrafindaki donme hizini belirleyen acisal hizdan turetilir bu sistemde pozitif degerler saat yonunun tersi donusu negatif degerler ise saat yonu donusunu gosterir Bu tur bir aciklama sag el koordinat sistemi temel alinarak yapilmistir Radial ve tegetsel hizlar Kartezyen hiz ve yer degistirme vektorlerinin bu vektorlerin radial ve tegetsel bilesenlere ayristirilmasiyla elde edilir Tegetsel hiz orijin merkezli bir cember uzerindeki hiz bilesenini belirtir v vT vR displaystyle boldsymbol v boldsymbol v T boldsymbol v R seklinde ifade edilir burada vT displaystyle boldsymbol v T tegetsel hizi vR displaystyle boldsymbol v R radial hizi gosterir Radial hiz veya radial hizin buyuklugu hiz vektoru ile radial yondeki birim vektor arasindaki nokta carpimi kullanilarak hesaplanir vR v r r v r displaystyle v R frac boldsymbol v cdot boldsymbol r left boldsymbol r right boldsymbol v cdot hat boldsymbol r burada r displaystyle boldsymbol r cismin pozisyonunu ve r displaystyle hat boldsymbol r radial yonu temsil eder Tegetsel hizin veya tegetsel hizin buyuklugunun degeri radial yonun birim vektoru ile hiz vektorunun capraz carpim sonucunun buyuklugu ile belirlenir Bu deger hiz vektorunun tegetsel yone gore nokta carpimi ya da acisal hiz w displaystyle omega ile yaricapin pozisyon vektorunun buyuklugu carpimi seklinde de ifade edilebilir vT r v r v t w r displaystyle v T frac boldsymbol r times boldsymbol v boldsymbol r boldsymbol v cdot hat boldsymbol t omega boldsymbol r su denklemlerle tanimlanir w r v r 2 displaystyle omega frac boldsymbol r times boldsymbol v boldsymbol r 2 Bu formuller tegetsel hizin ve ilgili acisal hizin hesaplanmasinda kullanilir ve nesnenin hareketinin geometrik ozelliklerini yansitarak dinamik analizler icin temel olusturur Acisal momentum skaler bir ifade olarak cismin kutlesi ile orijine olan uzakliginin ve bu uzaklik boyunca cismin tegetsel hizinin carpimi seklinde tanimlanir Alternatif olarak kutlenin uzakligin karesi ile acisal hizin carpimi olarak da ifade edilir Acisal momentum icin kullanilan isaret kurali acisal hiz icin belirlenen kuralla aynidir L mrvT mr2w displaystyle L mrv T mr 2 omega seklinde gosterilir burada m displaystyle m kutleyi r r displaystyle r boldsymbol r uzakligin buyuklugunu temsil eder mr2 displaystyle mr 2 terimi genel olarak eylemsizlik momenti olarak adlandirilir Eger kuvvetler sadece radial yonde etkiliyse ve bu kuvvetler mesafenin karesine ters orantiliysa ornegin gravitasyonel bir yorunge durumunda oldugu gibi acisal momentum degismez kalir Bu durumda tegetsel hiz mesafeye ters orantili olarak degisir acisal hiz mesafenin karesine ters orantilidir ve supurulen alanin orani sabit kalir Bu iliskiler Kepler in gezegensel hareket yasalari olarak tanimlanmistir Ayrica bakiniz Gorelilik kuraminda Minkowski uzayzamani icin tanimlanmis hizin bir cesidi Grup hizi Dalga paketlerinin yayilma hizi Cok yuksek hizlarda kullanilan terim Faz hizi Dalga fazlarinin yayilma hizi Gorelilikte yolcu zamanina gore tanimlanan hiz Gorelilik hizlarinda toplanabilir ozellikte bir hiz tanimi Terminal hizi Bir nesnenin serbest dususte ulasabilecegi maksimum hiz Akis hizi Bir akiskan icindeki hiz vektorlerinin dagilimi Hizin zamanla nasil degistigini gosteren grafik NotlarRobert Resnick and Jearl Walker Fundamentals of Physics Wiley 7 Sub edition June 16 2004 0 471 23231 9 Kaynakca The Feynman Lectures on Physics Vol I Ch 8 Motion www feynmanlectures caltech edu Erisim tarihi 5 Ocak 2024 Arsivlenmesi gereken baglantiya sahip kaynak sablonu iceren maddeler link David Halliday Robert Resnick Jearl Walker 2021 Fundamentals of Physics Extended 12 12sayfa 71 bas John Wiley amp Sons ISBN 978 1 119 77351 1 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 71 den alinti 29 Subat 2024 tarihinde Wayback Machine sitesinde Richard P Olenick Tom M Apostol David L Goodstein 2008 The Mechanical Universe Introduction to Mechanics and Heat illustrated reprinted bas Cambridge University Press s 84 ISBN 978 0 521 71592 8 3 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 84 ten alinti 6 Kasim 2023 tarihinde Wayback Machine sitesinde Michael J Cardamone 2007 Fundamental Concepts of Physics Universal Publishers s 5 ISBN 978 1 59942 433 0 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 5 ten alinti 2 Kasim 2023 tarihinde Wayback Machine sitesinde Jerry D Wilson Anthony J Buffa Bo Lou 2022 College Physics Essentials Eighth Edition Two Volume Set illustrated bas CRC Press s 40 ISBN 978 1 351 12991 6 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 40 tan alinti 2 Kasim 2023 tarihinde Wayback Machine sitesinde David Halliday Robert Resnick Jearl Walker 2021 Fundamentals of Physics Extended 12 12yayinci John Wiley amp Sons bas s 70 ISBN 978 1 119 77351 1 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 70 den alinti 27 Ekim 2023 tarihinde Wayback Machine sitesinde Adrian Banner 2007 The Calculus Lifesaver All the Tools You Need to Excel at Calculus illustrated bas Princeton University Press s 350 ISBN 978 0 691 13088 0 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 350 den alinti 29 Subat 2024 tarihinde Wayback Machine sitesinde a b Giri amp Bannerjee 2002 Statistical Tools and Technique Academic Publishers s 4 ISBN 978 81 87504 39 9 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 4 ten alinti 29 Subat 2024 tarihinde Wayback Machine sitesinde Bekir Karaoglu 2020 Classical Physics A Two Semester Coursebook Springer Nature s 41 ISBN 978 3 030 38456 2 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 41 den alinti 2 Kasim 2023 tarihinde Wayback Machine sitesinde David Halliday Robert Resnick Jearl Walker 2010 Fundamentals of Physics Chapters 33 37 John Wiley amp Sons s 1080 ISBN 978 0 470 54794 6 27 Ekim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 1080 den alinti 2 Kasim 2023 tarihinde Wayback Machine sitesinde Dunya nin atmosferi icin hava yogunlugu kullanilarak hesaplanir ve 0 C ile 1 atmosfer altinda 1 293 kg m3 degerindedir Jim Breithaupt 2000 New Understanding Physics for Advanced Level illustrated bas Nelson Thornes s 231 ISBN 978 0 7487 4314 8 29 Subat 2024 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 231 den alinti 2 Kasim 2023 tarihinde Wayback Machine sitesinde Eckehard W Mielke 2022 Modern Aspects Of Relativity World Scientific s 98 ISBN 978 981 12 4406 3 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 98 den alinti 2 Mart 2024 tarihinde Wayback Machine sitesinde 26 Kasim 2022 tarihinde kaynagindan arsivlendi Erisim tarihi 16 Nisan 2024 The Feynman Lectures on Physics Vol I Ch 9 Newton s Laws of Dynamics www feynmanlectures caltech edu Erisim tarihi 4 Ocak 2024 Arsivlenmesi gereken baglantiya sahip kaynak sablonu iceren maddeler link White F M 2008 Fluid mechanics The McGraw Hill Companies E Graham Aidan Burrows Brian Gaulter 2002 Mechanics Volume 6 illustrated bas Heinemann s 77 ISBN 978 0 435 51311 5 2 Kasim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 77 den alinti 2 Kasim 2023 tarihinde Wayback Machine sitesinde Anup Goel H J Sawant 2021 Engineering Mechanics Technical Publications s 8 ISBN 978 93 332 2190 0 27 Ekim 2023 tarihinde kaynagindan Erisim tarihi 16 Nisan 2024 Sayfa 8 den alinti 2 Kasim 2023 tarihinde Wayback Machine sitesinde Dis baglantilarWikimedia Commons ta Velocity ile ilgili ortam dosyalari bulunmaktadir Velocity and Acceleration Introduction to Mechanisms Carnegie Mellon University
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State







