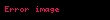Matematiğin bir alt dalı olan olasılık teorisinde bir martingal (veya martengal) ya da martingal süreci bir sonraki beklenen değerinin geçmişteki bütün gözlemlenmiş değerlerden bağımsız olarak şimdiki gözlemlenen değer olduğu bir stokastik süreçtir.
Martingal sözcüğü hakkında
Martingal sözü Türkçeye matematiksel anlamda yine aynı terimi kullanan İngilizce ve Fransızcadan Martingale sözüyle geçmiştir. Bu kavrama Türkçede karşılık bulmuş bir yerleşik bir terim yoktur. Olasılık teorisindeki martingal tanımını ilk defa 1934 yılında literatüre sokmuştur; ancak, martingal sözünü kullanmamıştır. Martingal sözünü bu yönde tezinde kullanan (1939) olmuştur ki o da Lévy'nin tanımını sürekli martingallere genişletmiştir. Martingalin matematiksel tanımını yine bu sözü kullanarak ilk defa vermiştir; Doob bu sözü Ville'in tezinde gördüğünden bir mülakatta bahsetmiştir. Martingal teorisinin bu aşamadan sonraki gelişiminde büyük pay sahibidir.
Martingal sözünün olasılık teorisinde yer alması büyük bir sürpriz değildir. öncesinde de olasılık kavramlarına aşina olan matematikçiler bu kavramı şans oyunlarında her zaman kazanan bahis stratejisi anlamına olan martingal sözünden biliyorlardı. Bu bahis stratejilerinin en basiti yazı-tura atmadaki bahsi kazanasaya kadar durmadan ikiye katlama stratejisidir.
Martingal sözünün etimolojisi hakkında kesinlik yoktur.
Tanım
Kesikli-zaman martingali
Bir rassal değişkenler dizisi 
;
.
Bir rassal değişkenler dizisinin başka bir rassal değişkenler dizisine göreceli olarak martingalini tanımlamak da mümkündür. Bu bağlamda yine 




;
.
Sürekli-zaman martingali



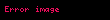

- Her
için,
,
'ye göre .
.
Eğer, 

Alt ve üst martingaller




Benzer bir şekilde, eşitsizlik aksi istimakette ise, 



Eğer 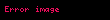

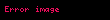

- Her
için,
,
'ye göre ölçülebilirdir.
.
.
Benzer bir şekilde, eşitsizlik aksi istimakette ise, yani aşağıdaki koşullar sağlanırsa, o zaman 

- Her
için,
,
'ye göre ölçülebilirdir.
.
.
Eğer, 

Özellikler
- Bir stokastik sürecin martingal olabilmesi için hem alt martingal hem de üst martingal olması gerekli ve yeterlidir.
- Eğer
martingalse, o zaman
sabittir.
alt martingal ise, o zaman
üst martingaldir.
- Eğer
alt (ya da üst) martingalse ve
ise, o zaman
de bir alt (ya da üst) martingaldir.
martingalse,
de
için martingaldir.
- Eğer
üst martingalse, o zaman
de bir üst martingaldir.
- Eğer
alt martingalse, o zaman
de bir alt martingaldir.
martingalse ve
, o zaman
sayesinde alt martingaldir. Eğer,
, o zaman
üst martingaldir.
- Genel olarak, bir martingal olmak zorunda değildir. Tersi ifade de genel olarak doğru değildir. Yani, bir Markov süreci genel olarak martingal olmak zorunda değildir.
- Sürekli her martingalin ya sonsuz varyasyonu vardır ya da bu martingal sabittir.
Örnekler
- Oyuncunun tura geldiğinde 1 lira kazandığı ama yazı geldiğinde 1 lira kaybettiği bir yazı-tura oyununu ele alalım.
- Eğer oyun adil bir parayla oynanıyorsa, o zaman oyuncunun herhangi bir adımdaki kazancı (oynanmış oyun sayısının fonksiyonu olarak) martingaldir.
- Eğer parada yazının gelme olasılığı daha yüksekse, o zaman oyuncunun herhangi bir adımdaki kazancı alt martingaldir.
- Eğer parada turanın gelme olasılığı daha yüksekse, o zaman oyuncunun herhangi bir adımdaki kazancı üst martingaldir.
- Eğer
integrallenebilir bir rassal değikense ve
olarak tanımlanırsa,
,
'e göre bir martingaldir. Gerçekten de,
olacaktır.
- yine martingaldir.
- Brown hareketi bir martingaldir.
- Eğer
Brown hareketiyse,
süreci martingaldir.
- Her
için,
süreci martingaldir.
Notlar
- ^ Uluğ Çapar da kitabında (Çapar 2013) Türkçe’de yerleşik bir karşılığı olmadığını belirterek söyleyişe daha uygun bulduğu martengal kelimesini kullanılmıştır.
- ^ YÖK Ulusal Tez Merkezi 9 Şubat 2014 tarihinde Wayback Machine sitesinde arşivlendi.'nde 15 Eylül 2024 tarihinde martengal ya da martingal sözü altında yapılan aramalarda elde edilen sonuçlarda martingal sözü kullanımı daha baskın gözükmektedir.
- ^ Ville 1939
- ^ Snell 1997
- ^ Mansuy 2009
Kaynakça
- Çapar, Uluğ (2013). Ölçü Kuramsal Olasılık ve Stokastik Kalkülüse Giriş. Ankara: .
- Ville, J. (1939), Gauthier-Villars (Ed.), Étude critique de la notion de collectif, Paris
- Snell, J. L. (1997). "A conversation with Joe Doob". Statist. Sci. 12 (4). ss. 301-311. Erişim tarihi: 4 Eylül 2024.
- Mansuy, Roger (June 2009). "The origins of the Word "Martingale"" (PDF). Electronic Journal for History of Probability and Statistics. 5 (1). 31 Ocak 2012 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 22 Ekim 2011.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan olasilik teorisinde bir martingal veya martengal ya da martingal sureci bir sonraki beklenen degerinin gecmisteki butun gozlemlenmis degerlerden bagimsiz olarak simdiki gozlemlenen deger oldugu bir stokastik surectir Martingal sozcugu hakkindaMartingal sozu Turkceye matematiksel anlamda yine ayni terimi kullanan Ingilizce ve Fransizcadan Martingale sozuyle gecmistir Bu kavrama Turkcede karsilik bulmus bir yerlesik bir terim yoktur Olasilik teorisindeki martingal tanimini ilk defa 1934 yilinda literature sokmustur ancak martingal sozunu kullanmamistir Martingal sozunu bu yonde tezinde kullanan 1939 olmustur ki o da Levy nin tanimini surekli martingallere genisletmistir Martingalin matematiksel tanimini yine bu sozu kullanarak ilk defa vermistir Doob bu sozu Ville in tezinde gordugunden bir mulakatta bahsetmistir Martingal teorisinin bu asamadan sonraki gelisiminde buyuk pay sahibidir Martingal sozunun olasilik teorisinde yer almasi buyuk bir surpriz degildir oncesinde de olasilik kavramlarina asina olan matematikciler bu kavrami sans oyunlarinda her zaman kazanan bahis stratejisi anlamina olan martingal sozunden biliyorlardi Bu bahis stratejilerinin en basiti yazi tura atmadaki bahsi kazanasaya kadar durmadan ikiye katlama stratejisidir Martingal sozunun etimolojisi hakkinda kesinlik yoktur TanimKesikli zaman martingali Bir rassal degiskenler dizisi Xn n N displaystyle X n n in mathbb N e asagidaki kosullar saglanirsa kesikli zaman martingali ya da kesikli martingal denir E Xn lt n N displaystyle mathsf E X n lt infty quad n in mathbb N E Xn 1 X1 Xn Xn n N displaystyle mathsf E X n 1 mid X 1 ldots X n X n quad n in mathbb N Bir rassal degiskenler dizisinin baska bir rassal degiskenler dizisine goreceli olarak martingalini tanimlamak da mumkundur Bu baglamda yine Yn n N displaystyle Y n n in mathbb N baska bir rassal degiskenler dizisi olsun Eger Xn n N displaystyle X n n in mathbb N ve Yn n N displaystyle Y n n in mathbb N asagidaki kosullari saglarsa o zaman Xn n N displaystyle X n n in mathbb N dizisine Yn n N displaystyle Y n n in mathbb N e gore martingaldir denir E Xn lt n N displaystyle mathsf E X n lt infty quad n in mathbb N E Xn 1 Y1 Yn Xn n N displaystyle mathsf E X n 1 mid Y 1 ldots Y n X n quad n in mathbb N Surekli zaman martingali W F P displaystyle Omega mathcal F mathbb P bir olasilik uzayi ve Ft t T displaystyle mathcal F t t in T de bu uzayin gercel sayilara bagli T R displaystyle T subset mathbb R filtresi olsun O zaman bir Xt t T displaystyle X t t in T stokastik surecine asagidaki kosullar saglanirsa Ft t T displaystyle mathcal F t t in T ye gore martingal denir Her t T displaystyle t in T icin Xt displaystyle X t Ft displaystyle mathcal F t ye gore E Xt lt t T displaystyle mathsf E X t lt infty quad t in T E Xt Fs Xs displaystyle mathsf E X t mid mathcal F s X s Eger Ft s Xs s t displaystyle mathcal F t sigma X s mid s leq t ise yani dogal filtreleme ise o zaman Xt displaystyle X t ye kisaca martingal denir Alt ve ust martingaller Xn n N displaystyle X n n in mathbb N ve Yn n N displaystyle Y n n in mathbb N rassal degisken dizileri verilmis olsun Asagidaki kosullar saglanirsa Xn n N displaystyle X n n in mathbb N dizisine Yn n N displaystyle Y n n in mathbb N e gore alt martingal denir E Xn lt n N displaystyle mathsf E X n lt infty quad n in mathbb N E Xn 1 Y1 Yn Xn n N displaystyle mathsf E X n 1 mid Y 1 ldots Y n geq X n quad n in mathbb N Benzer bir sekilde esitsizlik aksi istimakette ise Xn n N displaystyle X n n in mathbb N dizisine Yn n N displaystyle Y n n in mathbb N e gore ust martingal denir Yani asagidaki kosullar saglanirsa Xn n N displaystyle X n n in mathbb N dizisi Yn n N displaystyle Y n n in mathbb N e gore ust martingaldir E Xn lt n N displaystyle mathsf E X n lt infty quad n in mathbb N E Xn 1 Y1 Yn Xn n N displaystyle mathsf E X n 1 mid Y 1 ldots Y n leq X n quad n in mathbb N Eger Xt t T displaystyle X t t in T T R displaystyle T subset mathbb R bir stokastik surecse asagidaki kosullar saglandiginda Xt t T displaystyle X t t in T stokastik surecine Ft displaystyle mathcal F t ye gore alt martingal denir Her t T displaystyle t in T icin Xt displaystyle X t Ft displaystyle mathcal F t ye gore olculebilirdir E Xt lt t T displaystyle mathsf E X t lt infty quad t in T E Xt Fs Xs s t T s t displaystyle mathsf E X t mid mathcal F s geq X s quad forall s t in T s leq t Benzer bir sekilde esitsizlik aksi istimakette ise yani asagidaki kosullar saglanirsa o zaman Xt t T displaystyle X t t in T stokastik surecine Ft displaystyle mathcal F t ye gore ust martingal denir Her t T displaystyle t in T icin Xt displaystyle X t Ft displaystyle mathcal F t ye gore olculebilirdir E Xt lt t T displaystyle mathsf E X t lt infty quad t in T E Xt Fs Xs s t T s t displaystyle mathsf E X t mid mathcal F s leq X s quad forall s t in T s leq t Eger Ft s Xs s t displaystyle mathcal F t sigma X s mid s leq t ise yani dogal filtreleme ise o zaman Xt displaystyle X t stokastik surecine sagladigi esitsizlik kosuluna gore kisaca alt martingal ya da ust martingal denir OzelliklerBir stokastik surecin martingal olabilmesi icin hem alt martingal hem de ust martingal olmasi gerekli ve yeterlidir Eger Xt t T displaystyle X t t in T martingalse o zaman E Xt displaystyle mathsf E X t sabittir Xt t T displaystyle X t t in T alt martingal ise o zaman Xt t T displaystyle X t t in T ust martingaldir Eger Xt t T Yt t T displaystyle X t t in T Y t t in T alt ya da ust martingalse ve a b 0 displaystyle a b geq 0 ise o zaman aXt bYt t T displaystyle aX t bY t t in T de bir alt ya da ust martingaldir Xt t T Yt t T displaystyle X t t in T Y t t in T martingalse aXt bYt t T displaystyle aX t bY t t in T de a b R displaystyle a b in mathbb R icin martingaldir Eger Xt t T Yt t T displaystyle X t t in T Y t t in T ust martingalse o zaman min Xt Yt t T displaystyle min X t Y t t in T de bir ust martingaldir Eger Xt t T Yt t T displaystyle X t t in T Y t t in T alt martingalse o zaman max Xt Yt t T displaystyle max X t Y t t in T de bir alt martingaldir Xt t T displaystyle X t t in T martingalse ve f R R displaystyle f mathbb R to mathbb R o zaman f Xt t T displaystyle f X t t in T sayesinde alt martingaldir Eger f R R displaystyle f mathbb R to mathbb R o zaman f Xt t T displaystyle f X t t in T ust martingaldir Genel olarak bir martingal olmak zorunda degildir Tersi ifade de genel olarak dogru degildir Yani bir Markov sureci genel olarak martingal olmak zorunda degildir Surekli her martingalin ya sonsuz varyasyonu vardir ya da bu martingal sabittir OrneklerOyuncunun tura geldiginde 1 lira kazandigi ama yazi geldiginde 1 lira kaybettigi bir yazi tura oyununu ele alalim Eger oyun adil bir parayla oynaniyorsa o zaman oyuncunun herhangi bir adimdaki kazanci oynanmis oyun sayisinin fonksiyonu olarak martingaldir Eger parada yazinin gelme olasiligi daha yuksekse o zaman oyuncunun herhangi bir adimdaki kazanci alt martingaldir Eger parada turanin gelme olasiligi daha yuksekse o zaman oyuncunun herhangi bir adimdaki kazanci ust martingaldir Eger X displaystyle X integrallenebilir bir rassal degikense ve Xn E X Fn displaystyle X n E X mathcal F n olarak tanimlanirsa Xt n N displaystyle X t n in mathbb N Fn displaystyle mathcal F n e gore bir martingaldir Gercekten de E Xn 1 Fn E E X Fn 1 Fn E X Fn Xn displaystyle operatorname E X n 1 mathcal F n operatorname E operatorname E X mathcal F n 1 mathcal F n operatorname E X mathcal F n X n olacaktir yine martingaldir Brown hareketi bir martingaldir Eger Wt displaystyle W t Brown hareketiyse Wt2 t t 0 displaystyle W t 2 t t in 0 infty sureci martingaldir Her l R displaystyle lambda in mathbb R icin elWt 12tl2 t 0 displaystyle e lambda W t frac 1 2 t lambda 2 t in 0 infty sureci martingaldir Notlar Ulug Capar da kitabinda Capar 2013 Turkce de yerlesik bir karsiligi olmadigini belirterek soyleyise daha uygun buldugu martengal kelimesini kullanilmistir YOK Ulusal Tez Merkezi 9 Subat 2014 tarihinde Wayback Machine sitesinde arsivlendi nde 15 Eylul 2024 tarihinde martengal ya da martingal sozu altinda yapilan aramalarda elde edilen sonuclarda martingal sozu kullanimi daha baskin gozukmektedir Ville 1939 Snell 1997 Mansuy 2009KaynakcaCapar Ulug 2013 Olcu Kuramsal Olasilik ve Stokastik Kalkuluse Giris Ankara Ville J 1939 Gauthier Villars Ed Etude critique de la notion de collectif Paris Snell J L 1997 A conversation with Joe Doob Statist Sci 12 4 ss 301 311 Erisim tarihi 4 Eylul 2024 Mansuy Roger June 2009 The origins of the Word Martingale PDF Electronic Journal for History of Probability and Statistics 5 1 31 Ocak 2012 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 22 Ekim 2011
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans