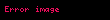İskenderiyeli Menelaus'a izafe edilen Menelaus teoremi düzlemsel geometride üçgenler üzerine bir teoremdir. , ve noktalarından oluşan üçgeninde , ve doğruları üzerinde bulunan ve üçgenin köşelerinden ayrık , ve noktalarının aynı doğru üzerinde olabilmesi ancak ve ancak:

denkleminin sağlanması ile mümkündür.
Bu denklemde, örneğin , eksi değer alabilen doğru parçalarını simgeler. Örnek olarak kesri sadece doğrusu kenarını kestiğinde artı değer alabilecek şekilde tanımlanmalıdır, çünkü sadece bu durumda iki doğru parçası aynı yönde ölçülmektedir ve bu durum diğer kesirler için de geçerlidir. Matematikçiler arasında bu teoremin yanlış olduğu üzerine süregelen bir şaka vardır (bunun yerine Ceva teoreminin kullanılması gerektiği söylenir).
İspatı

Aşağıda teoremin pek çok ispatından bir tanesi verilmiştir. Öncelikle, denklemin sol tarafının işareti kontrol edilebilir. 

Daha sonra büyüklük kontrol edilebilir. DEF doğrusunu 









Son olarak teoremin denkleminin doğruluğu durumunda 





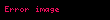



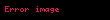


Bu da 





Batlamyus Almagest adlı eserinde Menelaus teoremini kuramının temeli olarak kullanmıştır.
Ayrıca bakınız
Dış bağlantılar
- . 22 Aralık 2017 tarihinde kaynağından arşivlendi., Menelaos teoreminin ispatı @PlanetMath
- . 9 Ağustos 2018 tarihinde kaynağından arşivlendi., Ceva'dan Menelaus'a @cut-the-knot.org
- . 9 Ağustos 2018 tarihinde kaynağından arşivlendi., Ceva ve Menelaus yolda karşılaşırlar @cut-the-knot.org
- "Menelaus and Ceva". MathPages. Erişim tarihi: 25 Ocak 2021.
- Warendorff, Jay. . . 9 Ağustos 2018 tarihinde kaynağından arşivlendi..
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Iskenderiyeli Menelaus a izafe edilen Menelaus teoremi duzlemsel geometride ucgenler uzerine bir teoremdir A displaystyle A B displaystyle B ve C displaystyle C noktalarindan olusan ABC displaystyle triangle ABC ucgeninde BC displaystyle BC AC displaystyle AC ve AB displaystyle AB dogrulari uzerinde bulunan ve ucgenin koselerinden ayrik D displaystyle D E displaystyle E ve F displaystyle F noktalarinin ayni dogru uzerinde olabilmesi ancak ve ancak Menelaus teoremi durum 1 DEF dogrsu ABC ucgeninin icinden gecerAFFB BDDC CEEA 1 displaystyle frac AF FB cdot frac BD DC cdot frac CE EA 1 denkleminin saglanmasi ile mumkundur Bu denklemde ornegin AB displaystyle AB eksi deger alabilen dogru parcalarini simgeler Ornek olarak AFFB displaystyle frac AF FB kesri sadece DEF displaystyle DEF dogrusu AB displaystyle AB kenarini kestiginde arti deger alabilecek sekilde tanimlanmalidir cunku sadece bu durumda iki dogru parcasi ayni yonde olculmektedir ve bu durum diger kesirler icin de gecerlidir Matematikciler arasinda bu teoremin yanlis oldugu uzerine suregelen bir saka vardir bunun yerine Ceva teoreminin kullanilmasi gerektigi soylenir IspatiMenelaus teoremi durum 2 DEF dogrusu ABC ucgeninin tamamen disindadir Asagida teoremin pek cok ispatindan bir tanesi verilmistir Oncelikle denklemin sol tarafinin isareti kontrol edilebilir DEF displaystyle DEF cizgisi ABC displaystyle triangle ABC ucgeninin kenarlarini cift sayida kesmelidir ucgenin icinden gecerse iki kere ust resim ya da ucgenin icinden gecmezse sifir kere alt resim Dolayisiyla daima tek sayida eksi deger olacagindan sonuc eksi olacaktir Daha sonra buyukluk kontrol edilebilir DEF dogrusunu A displaystyle A B displaystyle B ve C displaystyle C koselerine birlestiren dikmeler olusturalim DEF displaystyle DEF yi taban kabul edelim ve A displaystyle A B displaystyle B ve C displaystyle C dikmelerinin yuksekliklerini a displaystyle a b displaystyle b ve c displaystyle c olarak tanimlayalim Benzer ucgenler kullanilarak denklemin sol tarafi asagidaki gibi sadelesir ab bc ca 1 displaystyle left frac a b cdot frac b c cdot frac c a right 1 Son olarak teoremin denkleminin dogrulugu durumunda D displaystyle D E displaystyle E F displaystyle F noktalarinin dogrusal olmasi gerektigi celiski kullanilarak ispatlanabilir AB displaystyle AB kenari uzerinde F displaystyle F den farkli bir F displaystyle F noktasi oldugunu varsayalim ve AF displaystyle AF AF displaystyle AF ve AB displaystyle AB dogru parcalarinin uzunluklarini n displaystyle n n displaystyle n ve s displaystyle s olarak tanimlayalim F displaystyle F noktasinin da denklemi dogruladigini varsayalim Bu durumda asagidaki kesirler esit degerde olacaktir AFFB AF F B displaystyle frac AF FB frac AF F B ns n n s n displaystyle frac n s n frac n s n Bu da n n displaystyle n n esitligine sadelesir Bu da AB displaystyle AB dogrusu uzerinde yalnizca tek bir noktanin denklemi dogrulayabildigini kanitlar ve bu nokta da D displaystyle D ve E displaystyle E ile ayni dogru uzerinde bulunmalidir Simetriden dolayi ayni durum D displaystyle D ve E displaystyle E noktalari icin de gecerlidir Batlamyus Almagest adli eserinde Menelaus teoremini kuraminin temeli olarak kullanmistir Ayrica bakinizCeva teoremi Kenarortay geometri Dis baglantilar 22 Aralik 2017 tarihinde kaynagindan arsivlendi Menelaos teoreminin ispati PlanetMath 9 Agustos 2018 tarihinde kaynagindan arsivlendi Ceva dan Menelaus a cut the knot org 9 Agustos 2018 tarihinde kaynagindan arsivlendi Ceva ve Menelaus yolda karsilasirlar cut the knot org Menelaus and Ceva MathPages Erisim tarihi 25 Ocak 2021 Warendorff Jay 9 Agustos 2018 tarihinde kaynagindan arsivlendi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State