Moskova Matematik Papirüsü, Mısır dışındaki ilk sahibi olan Eski Mısır bilimci Vladimir Golenishchev'in ardından Golenishchev Matematik Papirüsü olarak da adlandırılan eski bir Mısır matematik papirüsüdür. Golenishchev papirüsü 1892 veya 1893'te Teb'de satın alındı. Daha sonra bugün kaldığı Moskova'daki Puşkin Devlet Güzel Sanatlar Müzesi koleksiyonuna girdi.

Hiyeratik (Resim yazısı ile yazılmış) metnin paleografisine (eski yazı bilimi) ve ortografisine (yazım ve imlasına) dayanarak, metin büyük olasılıkla 13. Hanedanlığa yazılmıştır ve muhtemelen Mısır'ın 12. Hanedanlığı'na, kabaca MÖ 1850'ye tarihlenen daha eski materyallere dayanmaktadır. Yaklaşık 5½ m (18 ft) uzunluğunda ve 3,8 ile 7,6 cm (1,5 ve 3 inç) arasında değişen genişlikte sayfa düzeni, 1930'da Sovyet Doğubilimci Vasily Vasilievich Struve tarafından çözümlerle 25 probleme bölünmüştür. İyi bilinen matematiksel bir papirüstür ve genellikle Rhind Papirüsü ile birlikte anılır. Moskova Matematik Papirüsü, Rhind Papirüsü'nden daha eski ancak daha küçüktür.
Moskova Papirüsünde yer alan egzersizler
Moskova Papirüsündeki problemler, belirli bir sırayı takip etmez ve problemlerin çözümleri Rhind Papirüs'ündekinden çok daha az ayrıntı sağlar. Papirüs, bazı geometri problemleriyle tanınır. Problem 10 ve 14, sırasıyla bir yüzey alanını ve bir kesik kısmın hacmini hesaplamakla ilgilidir. Geri kalan sorunlar doğada daha yaygındır.
Gemi parçası problemleri
2. ve 3. problemler, geminin parçası problemleridir. Problemlerden biri, bir geminin dümeninin uzunluğunu hesaplarken, diğeri, orijinal olarak 30 arşın uzunluğunda bir sedir kütüğünün uzunluğunun 1/3 + 1/5'i olan bir gemi direğinin uzunluğunu hesaplar.
Aha problemleri
| Hiyeroglif olarak: Aha |
| {{{2}}} |
Aha problemleri, miktarı ve parçalarının toplamı verilen bilinmeyen miktarları (Aha olarak anılır) bulmayı içerir. Rhind Papirüsü ayrıca bu tür problemlerden dördünü içerir. Moskova Papirüsünün 1, 19 ve 25. problemleri Aha problemleridir. Örneğin 19. problem, birinden 1 ve ½ kez alınan ve 10 yapmak için 4'e eklenen bir miktarın hesaplanmasını ister. Başka bir deyişle, modern matematiksel gösterimde birinden 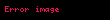
Pefsu problemleri
Problemlerin çoğu pefsu problemleridir (bakınız: ): 25 problemden 10'u. Bir pefsu, tahıl hekat'ından (antik Mısır hacim birimi) yapılan biranın gücünü ölçer:

(1) pefsu 20'nin 100 somun ekmek hesaplama örneği (2) Biri size: "pefsu 20'nin 100 somun ekmeğiniz var (3) pefsu 4 birası ile değiştirilmek için (4) 1/2 1/4 maltlık bira gibi" (5) Önce pefsu 20'nin 100 somun ekmeği için gerekli olan tahıl miktarını hesaplayın (6) Sonuç 5 hekattır. O zaman 1/2 1/4 maltlık bira denilen biradan bir sürahi bira için neye ihtiyacınız olduğunu düşünün (7) Sonuç, Yukarı Mısır tahılından yapılan sürahi birası için gereken hekat ölçüsünün 1/2'sidir. (8) 5 hekatın 1/2'sini hesaplayın, sonuç 2 1/2 olacaktır (9) Bunu 2 1/2 dört kez al (10) Sonuç 10'dur. Sonra ona şöyle dersiniz: (11) "Bakın! Bira miktarının doğru olduğu görülüyor."
Baku problemleri
11. ve 23. problemler Baku problemleridir. Bunlar, işçilerin çıktısını hesaplar. Problem 11, bir kişinin 5'e 5 ölçülerinde 100 kütük getirdiği durumda, buna karşılık 4'e 4 ölçülerde kaç kütük getirebileceğini sorar. Problem 23, sandaletleri kesmesi ve süslemesi gereken bir kunduracının çıkarttığı işi bulur.
Geometri problemleri
Yirmi beş problemin yedisi geometri problemleridir ve üçgenlerin alanlarını hesaplamadan bir yarım kürenin yüzey alanını (problem 10) ve kesik bir piramitin hacmini bulmaya kadar uzanır.
İki Geometri Problemi
Problem 10
Moskova Matematik Papirüsünün 10. problemi, bir yarım kürenin (Struve, Gillings) veya muhtemelen bir yarım silindirin (Peet) yüzey alanının hesaplanmasını ister. Aşağıda, sorunun bir yarım kürenin alanıyla ilgili olduğunu varsayıyoruz.
Problem 10'un metni şu şekilde çalışır: "Bir sepet hesaplama örneği. Size ağzı 4 1/2 olan bir sepet verilir. Bunun yüzeyi nedir? Sepet, yarım yumurta kabuğu gibi olduğu için 9'un 1/9'unu alın. 1 bulursun. Kalanı hesaplayın, 8 bulunurr. 8'in 1/9'unu hesaplayın. 2/3 + 1/6 + 1/18 elde edersiniz. 2/3 + 1/6 + 1/18'i çıkardıktan sonra bu 8'in kalanını bulun. 7 + 1/9 bulursun. 7 + 1/9'u 4 + 1/2 ile çarpın. 32 bulursun. Bakın burası onun alanıdır. Doğru buldunuz."
Çözüm, alanı şu şekilde hesaplamaktır: 
Bu, Moskova Papirüsünü yazanın 
Problem 14: Kesik kare piramidin hacmi

Moskova Matematiksel Papirüsü'nün 14. problemi, bir kesik cismin (frustum) hacmini hesaplar.
Problem 14, bir piramidin, gösterildiği gibi üst alanın 2 birim uzunluğunda bir kare, alt tarafın 4 birim uzunluğunda bir kare ve yüksekliğinin 6 birim olacağı şekilde kesildiğini belirtir. Hacmin 56 kübik birim olduğu görülmüştür ki bu doğrudur.
Örneğin metni şu şekilde çalışır: "Size söylenirse: dikey yüksekliği 6'dan oluşan kesilmiş bir piramit, dikey yükseklik için tabanda 4, üstte 2: 4'ün karesini alacaksınız; sonuç 16. 4'ü ikiye katlayacaksınız; sonuç 8. Bu 2'nin karesini alacaksınız; sonuç 4. 16'yı, 8'i ve 4'ü eklemelisiniz; sonuç 28. 6'nın 1/3'ünü alacaksınız; sonuç 2. 28'i iki kez alacaksınız; sonuç 56. Bak, bu 56. [Onu] doğru bulacaksın."
Problemin çözümü, Mısırlıların kesik bir piramidin hacmini elde etmek için doğru formülü bildiklerini gösteriyor:

a ve b, kesik piramidin taban ve üst kenar uzunlukları ve h, yüksekliği olmak üzere. Araştırmacılar, Mısırlıların kesik bir cismin (frustum) hacmi formülüne nasıl ulaşmış olabileceklerini tahmin etmişlerdir, ancak bu formülün türetilmesi papirüste verilmemiştir.
Özet
Richard J. Gillings, Papirüs'ün içeriğinin üstünkörü bir özetini verdi Üstü çizili sayılar, payda olarak bu sayıya sahip birim kesri belirtir. örneğin; 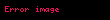
| No. | İçerik detayı. |
|---|---|
| 1 | Hasarlı ve okunamaz durumda. |
| 2 | Hasarlı ve okunamaz durumda. |
| 3 | Bir sedir direği.  'un 'un  'i 'i  . Belirsiz. . Belirsiz. |
| 4 | Bir üçgenin alanı. 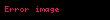 'un 'un  'si 'si 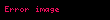 . . |
| 5 | Somun ve ekmek pesusu. No. 8'e benzer. |
| 6 | Dikdörtgen, Alan  . . 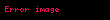 ve ve  'yi bul. 'yi bul. |
| 7 | Üçgen, Alan  . .  ve ve  'yi bul. 'yi bul. |
| 8 | Somun ve ekmek pesusu. |
| 9 | Somun ve ekmek pesusu. |
| 10 | Yarım kürenin (veya silindirin) eğimli yüzey alanı. |
| 11 | Somun ve sepet. Belirsiz. |
| 12 | Bira pesusu. Belirsiz. |
| 13 | PSomun ve ekmek pesusu. No. 9'a benzer. |
| 14 | Kesik bir piramidin hacmi. 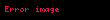 . . |
| 15 | Bira pesusu. |
| 16 | Bira pesusu. No. 15'e benzer. |
| 17 | Üçgen, Alan  . .  ve ve  'yi bul. 'yi bul. |
| 18 | Kıyafetlerin arşın ve avuç içi ile ölçümü. Belirsiz. |
| 19 | Denklemi çözün,  . Net. . Net. |
| 20 |  somun pesusu. Horus-gözü kesirleri. somun pesusu. Horus-gözü kesirleri. |
| 21 | Kurbanlık ekmeğin karıştırılması. |
| 22 | Somun ve bira pesusu. Takas. |
| 23 | Bir ayakkabı tamircisinin işini hesaplamak. Belirsiz. Peet çok zor der. |
| 24 | Somun ve bira takası. |
| 25 | Denklemi çözün,  . Basit ve net. . Basit ve net. |
Diğer Matematiksel Papirüsler
Eski Mısır'dan diğer matematiksel metinler şunları içerir:
Notlar
- ^ a b c d e f g h i Clagett, Marshall. 1999. Ancient Egyptian Science: A Source Book. Volume 3: Ancient Egyptian Mathematics. Memoirs of the American Philosophical Society 232. Philadelphia: American Philosophical Society.
- ^ Struve, Vasilij Vasil'evič, and . 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
- ^ . 13 Şubat 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Eylül 2020.
- ^ Great Soviet Encyclopedia, 3rd edition, entry on "Папирусы математические", available online here
- ^ Williams, Scott W. Egyptian Mathematical Papyri 18 Şubat 2020 tarihinde Wayback Machine sitesinde .
- ^ as given in Gunn & Peet, Journal of Egyptian Archaeology, 1929, 15: 176. See also, Van der Waerden, 1961, Plate 5
- ^ Gillings, R. J. (1964), "The volume of a truncated pyramid in ancient Egyptian papyri", The Mathematics Teacher, 57 (8), ss. 552-555, JSTOR 27957144,
While it has been generally accepted that the Egyptians were well acquainted with the formula for the volume of the complete square pyramid, it has not been easy to establish how they were able to deduce the formula for the truncated pyramid, with the mathematics at their disposal, in its most elegant and far from obvious form
. - ^ Gillings, Richard J. (1982). Mathematics in the Time of the Pharoahs. Dover. ss. 246-247. ISBN .
Dipnotlar
- ^ Bu tablo, Gillings'in "Firavunlar Zamanında Matematik (İngilizce: Mathematics in the Time of the Pharoahs)", ss. 246-247'nin kelimesi kelimesine bir kopyasıdır. Yalnızca diğer bölümlere yapılan atıflar atlanmıştır. Pesu problemleri hakkındaki 5, 8-9, 13, 15, 20-22 ve 24 numaralı problemlerin açıklamalarının bilgileri "Bkz. Bölüm 12" ile sonuçlanmıştır. Doğrusal ve ikinci dereceden denklemler hakkındaki problem 19'un açıklamasının bilgileri "Bkz. Bölüm 14" ile sonuçlanmıştır. Yarım silindirlerin veya yarım kürelerin yüzey alanları hakkındaki problem 10 ve 14'ün açıklamalarının bilgileri "Bkz. Bölüm 18" ile sonuçlanmıştır.
Kaynakça
Moskova Matematik Papirüsünün Tam Metni
- Struve, Vasilij Vasil'evič, and . 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
Diğer Kaynaklar
- Allen, Don. Nisan 2001. The Moscow Papyrus27 Mart 2018 tarihinde Wayback Machine sitesinde . and Summary of Egyptian Mathematics3 Mart 2016 tarihinde Wayback Machine sitesinde ..
- , Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Wiesbaden 2003.
- Mathpages.com. The Prismoidal Formula31 Ocak 2020 tarihinde Wayback Machine sitesinde ..
- O'Connor and Robertson, 2000. Mathematics in Egyptian Papyri12 Ocak 2012 tarihinde Wayback Machine sitesinde ..
- Truman State University, Math and Computer Science Division. Mathematics and the Liberal Arts: Ancient Egypt18 Şubat 2013 tarihinde Wayback Machine sitesinde . and The Moscow Mathematical Papyrus13 Mayıs 2012 tarihinde Wayback Machine sitesinde ..
- Williams, Scott W. Mathematicians of the African Diaspora5 Temmuz 2020 tarihinde Wayback Machine sitesinde ., containing a page on Egyptian Mathematics Papyri7 Nisan 2015 tarihinde Wayback Machine sitesinde ..
- Zahrt, Kim R. W. Thoughts on Ancient Egyptian Mathematics27 Eylül 2011 tarihinde Wayback Machine sitesinde ..
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Moskova Matematik Papirusu Misir disindaki ilk sahibi olan Eski Misir bilimci Vladimir Golenishchev in ardindan Golenishchev Matematik Papirusu olarak da adlandirilan eski bir Misir matematik papirusudur Golenishchev papirusu 1892 veya 1893 te Teb de satin alindi Daha sonra bugun kaldigi Moskova daki Puskin Devlet Guzel Sanatlar Muzesi koleksiyonuna girdi Moskova da Puskin Guzel Sanatlar Devlet Muzesi nde bulunan Moskova Matematik Papirusunun 14 problemi V Struve 1930 Misir in Ikinci Ara Donemine 13 hanedan ait Thebes menseli hiyeratik bir papirustur Hiyeratik Resim yazisi ile yazilmis metnin paleografisine eski yazi bilimi ve ortografisine yazim ve imlasina dayanarak metin buyuk olasilikla 13 Hanedanliga yazilmistir ve muhtemelen Misir in 12 Hanedanligi na kabaca MO 1850 ye tarihlenen daha eski materyallere dayanmaktadir Yaklasik 5 m 18 ft uzunlugunda ve 3 8 ile 7 6 cm 1 5 ve 3 inc arasinda degisen genislikte sayfa duzeni 1930 da Sovyet Dogubilimci Vasily Vasilievich Struve tarafindan cozumlerle 25 probleme bolunmustur Iyi bilinen matematiksel bir papirustur ve genellikle Rhind Papirusu ile birlikte anilir Moskova Matematik Papirusu Rhind Papirusu nden daha eski ancak daha kucuktur Moskova Papirusunde yer alan egzersizlerMoskova Papirusundeki problemler belirli bir sirayi takip etmez ve problemlerin cozumleri Rhind Papirus undekinden cok daha az ayrinti saglar Papirus bazi geometri problemleriyle taninir Problem 10 ve 14 sirasiyla bir yuzey alanini ve bir kesik kismin hacmini hesaplamakla ilgilidir Geri kalan sorunlar dogada daha yaygindir Gemi parcasi problemleri 2 ve 3 problemler geminin parcasi problemleridir Problemlerden biri bir geminin dumeninin uzunlugunu hesaplarken digeri orijinal olarak 30 arsin uzunlugunda bir sedir kutugunun uzunlugunun 1 3 1 5 i olan bir gemi direginin uzunlugunu hesaplar Aha problemleri Hiyeroglif olarak Aha 2 Aha problemleri miktari ve parcalarinin toplami verilen bilinmeyen miktarlari Aha olarak anilir bulmayi icerir Rhind Papirusu ayrica bu tur problemlerden dordunu icerir Moskova Papirusunun 1 19 ve 25 problemleri Aha problemleridir Ornegin 19 problem birinden 1 ve kez alinan ve 10 yapmak icin 4 e eklenen bir miktarin hesaplanmasini ister Baska bir deyisle modern matematiksel gosterimde birinden 32x 4 10 displaystyle frac 3 2 x 4 10 denklemini cozmesi istenir Pefsu problemleri Problemlerin cogu pefsu problemleridir bakiniz 25 problemden 10 u Bir pefsu tahil hekat indan antik Misir hacim birimi yapilan biranin gucunu olcer pefsu somun ekmek veya surahi bira sayisitahil hekat sayisi displaystyle mbox pefsu frac mbox somun ekmek veya surahi bira sayisi mbox tahil hekat sayisi 1 pefsu 20 nin 100 somun ekmek hesaplama ornegi 2 Biri size pefsu 20 nin 100 somun ekmeginiz var 3 pefsu 4 birasi ile degistirilmek icin 4 1 2 1 4 maltlik bira gibi 5 Once pefsu 20 nin 100 somun ekmegi icin gerekli olan tahil miktarini hesaplayin 6 Sonuc 5 hekattir O zaman 1 2 1 4 maltlik bira denilen biradan bir surahi bira icin neye ihtiyaciniz oldugunu dusunun 7 Sonuc Yukari Misir tahilindan yapilan surahi birasi icin gereken hekat olcusunun 1 2 sidir 8 5 hekatin 1 2 sini hesaplayin sonuc 2 1 2 olacaktir 9 Bunu 2 1 2 dort kez al 10 Sonuc 10 dur Sonra ona soyle dersiniz 11 Bakin Bira miktarinin dogru oldugu goruluyor Baku problemleri 11 ve 23 problemler Baku problemleridir Bunlar iscilerin ciktisini hesaplar Problem 11 bir kisinin 5 e 5 olculerinde 100 kutuk getirdigi durumda buna karsilik 4 e 4 olculerde kac kutuk getirebilecegini sorar Problem 23 sandaletleri kesmesi ve suslemesi gereken bir kunduracinin cikarttigi isi bulur Geometri problemleri Yirmi bes problemin yedisi geometri problemleridir ve ucgenlerin alanlarini hesaplamadan bir yarim kurenin yuzey alanini problem 10 ve kesik bir piramitin hacmini bulmaya kadar uzanir Iki Geometri ProblemiProblem 10 Moskova Matematik Papirusunun 10 problemi bir yarim kurenin Struve Gillings veya muhtemelen bir yarim silindirin Peet yuzey alaninin hesaplanmasini ister Asagida sorunun bir yarim kurenin alaniyla ilgili oldugunu varsayiyoruz Problem 10 un metni su sekilde calisir Bir sepet hesaplama ornegi Size agzi 4 1 2 olan bir sepet verilir Bunun yuzeyi nedir Sepet yarim yumurta kabugu gibi oldugu icin 9 un 1 9 unu alin 1 bulursun Kalani hesaplayin 8 bulunurr 8 in 1 9 unu hesaplayin 2 3 1 6 1 18 elde edersiniz 2 3 1 6 1 18 i cikardiktan sonra bu 8 in kalanini bulun 7 1 9 bulursun 7 1 9 u 4 1 2 ile carpin 32 bulursun Bakin burasi onun alanidir Dogru buldunuz Cozum alani su sekilde hesaplamaktir Alan 2 89 2 cap 2 25681 cap 2 displaystyle text Alan left frac 2 times 8 9 right 2 times text cap 2 frac 256 81 text cap 2 Bu Moskova Papirusunu yazanin 25681 3 16049 displaystyle frac 256 81 approx 3 16049 u yaklasik p degeri olarak kullandigi anlamina gelir Problem 14 Kesik kare piramidin hacmi Moskova Matematiksel Papirusu nun 14 problemi bir kesik cismin frustum hacmini hesaplar Problem 14 bir piramidin gosterildigi gibi ust alanin 2 birim uzunlugunda bir kare alt tarafin 4 birim uzunlugunda bir kare ve yuksekliginin 6 birim olacagi sekilde kesildigini belirtir Hacmin 56 kubik birim oldugu gorulmustur ki bu dogrudur Ornegin metni su sekilde calisir Size soylenirse dikey yuksekligi 6 dan olusan kesilmis bir piramit dikey yukseklik icin tabanda 4 ustte 2 4 un karesini alacaksiniz sonuc 16 4 u ikiye katlayacaksiniz sonuc 8 Bu 2 nin karesini alacaksiniz sonuc 4 16 yi 8 i ve 4 u eklemelisiniz sonuc 28 6 nin 1 3 unu alacaksiniz sonuc 2 28 i iki kez alacaksiniz sonuc 56 Bak bu 56 Onu dogru bulacaksin Problemin cozumu Misirlilarin kesik bir piramidin hacmini elde etmek icin dogru formulu bildiklerini gosteriyor V 13h a2 ab b2 displaystyle V frac 1 3 h a 2 ab b 2 a ve b kesik piramidin taban ve ust kenar uzunluklari ve h yuksekligi olmak uzere Arastirmacilar Misirlilarin kesik bir cismin frustum hacmi formulune nasil ulasmis olabileceklerini tahmin etmislerdir ancak bu formulun turetilmesi papiruste verilmemistir OzetRichard J Gillings Papirus un iceriginin ustunkoru bir ozetini verdi Ustu cizili sayilar payda olarak bu sayiya sahip birim kesri belirtir ornegin 4 14 displaystyle bar 4 frac 1 4 birim kesirler eski Misir matematiginde ortak calisma nesneleriydi Moskova Matematik Papirusunun Icerigi No Icerik detayi 1 Hasarli ve okunamaz durumda 2 Hasarli ve okunamaz durumda 3 Bir sedir diregi 30 displaystyle 30 un 3 5 displaystyle bar 3 bar 5 i 16 displaystyle 16 Belirsiz 4 Bir ucgenin alani 4 10 displaystyle 4 times 10 un 2 displaystyle bar 2 si 20 displaystyle 20 5 Somun ve ekmek pesusu No 8 e benzer 6 Dikdortgen Alan 12 b 2 4 l displaystyle 12 b bar 2 bar 4 l l displaystyle l ve b displaystyle b yi bul 7 Ucgen Alan 20 h 22 b displaystyle 20 h 2 bar 2 b h displaystyle h ve b displaystyle b yi bul 8 Somun ve ekmek pesusu 9 Somun ve ekmek pesusu 10 Yarim kurenin veya silindirin egimli yuzey alani 11 Somun ve sepet Belirsiz 12 Bira pesusu Belirsiz 13 PSomun ve ekmek pesusu No 9 a benzer 14 Kesik bir piramidin hacmi V h 3 a2 ab b2 displaystyle V h 3 a 2 ab b 2 15 Bira pesusu 16 Bira pesusu No 15 e benzer 17 Ucgen Alan 20 b 3 15 h displaystyle 20 b bar 3 bar 15 h h displaystyle h ve b displaystyle b yi bul 18 Kiyafetlerin arsin ve avuc ici ile olcumu Belirsiz 19 Denklemi cozun 12 x 4 10 displaystyle 1 bar 2 x 4 10 Net 20 1 000 displaystyle 1 000 somun pesusu Horus gozu kesirleri 21 Kurbanlik ekmegin karistirilmasi 22 Somun ve bira pesusu Takas 23 Bir ayakkabi tamircisinin isini hesaplamak Belirsiz Peet cok zor der 24 Somun ve bira takasi 25 Denklemi cozun 2x x 9 displaystyle 2x x 9 Basit ve net Diger Matematiksel PapiruslerEski Misir dan diger matematiksel metinler sunlari icerir Berlin Papirusu 6619 Rhind PapirusuNotlar a b c d e f g h i Clagett Marshall 1999 Ancient Egyptian Science A Source Book Volume 3 Ancient Egyptian Mathematics Memoirs of the American Philosophical Society 232 Philadelphia American Philosophical Society 0 87169 232 5 Struve Vasilij Vasil evic and 1930 Mathematischer Papyrus des Staatlichen Museums der Schonen Kunste in Moskau Quellen und Studien zur Geschichte der Mathematik Abteilung A Quellen 1 Berlin J Springer 13 Subat 2012 tarihinde kaynagindan arsivlendi Erisim tarihi 3 Eylul 2020 Great Soviet Encyclopedia 3rd edition entry on Papirusy matematicheskie available online here Williams Scott W Egyptian Mathematical Papyri 18 Subat 2020 tarihinde Wayback Machine sitesinde as given in Gunn amp Peet Journal of Egyptian Archaeology 1929 15 176 See also Van der Waerden 1961 Plate 5 Gillings R J 1964 The volume of a truncated pyramid in ancient Egyptian papyri The Mathematics Teacher 57 8 ss 552 555 JSTOR 27957144 While it has been generally accepted that the Egyptians were well acquainted with the formula for the volume of the complete square pyramid it has not been easy to establish how they were able to deduce the formula for the truncated pyramid with the mathematics at their disposal in its most elegant and far from obvious form Gillings Richard J 1982 Mathematics in the Time of the Pharoahs Dover ss 246 247 ISBN 9780486243153 Dipnotlar Bu tablo Gillings in Firavunlar Zamaninda Matematik Ingilizce Mathematics in the Time of the Pharoahs ss 246 247 nin kelimesi kelimesine bir kopyasidir Yalnizca diger bolumlere yapilan atiflar atlanmistir Pesu problemleri hakkindaki 5 8 9 13 15 20 22 ve 24 numarali problemlerin aciklamalarinin bilgileri Bkz Bolum 12 ile sonuclanmistir Dogrusal ve ikinci dereceden denklemler hakkindaki problem 19 un aciklamasinin bilgileri Bkz Bolum 14 ile sonuclanmistir Yarim silindirlerin veya yarim kurelerin yuzey alanlari hakkindaki problem 10 ve 14 un aciklamalarinin bilgileri Bkz Bolum 18 ile sonuclanmistir KaynakcaMoskova Matematik Papirusunun Tam Metni Struve Vasilij Vasil evic and 1930 Mathematischer Papyrus des Staatlichen Museums der Schonen Kunste in Moskau Quellen und Studien zur Geschichte der Mathematik Abteilung A Quellen 1 Berlin J SpringerDiger Kaynaklar Allen Don Nisan 2001 The Moscow Papyrus27 Mart 2018 tarihinde Wayback Machine sitesinde and Summary of Egyptian Mathematics3 Mart 2016 tarihinde Wayback Machine sitesinde Agyptische Algorithmen Eine Untersuchung zu den mittelagyptischen mathematischen Aufgabentexten Wiesbaden 2003 Mathpages com The Prismoidal Formula31 Ocak 2020 tarihinde Wayback Machine sitesinde O Connor and Robertson 2000 Mathematics in Egyptian Papyri12 Ocak 2012 tarihinde Wayback Machine sitesinde Truman State University Math and Computer Science Division Mathematics and the Liberal Arts Ancient Egypt18 Subat 2013 tarihinde Wayback Machine sitesinde and The Moscow Mathematical Papyrus13 Mayis 2012 tarihinde Wayback Machine sitesinde Williams Scott W Mathematicians of the African Diaspora5 Temmuz 2020 tarihinde Wayback Machine sitesinde containing a page on Egyptian Mathematics Papyri7 Nisan 2015 tarihinde Wayback Machine sitesinde Zahrt Kim R W Thoughts on Ancient Egyptian Mathematics27 Eylul 2011 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans