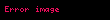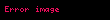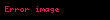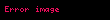Pascal üçgeni, matematikte binom katsayılarını içeren üçgensel bir dizidir. Fransız matematikçi Blaise Pascal'ın soyadıyla anılsa da Pascal'dan önce Hindistan, İran, Çin, Almanya ve İtalya'da matematikçiler tarafından çalışılmıştır.

Genellikle Pascal üçgeninin satırları üstten n=0'dan başlayarak numaralandırılır ve her satırdaki sayılar ise soldan itibaren k=0'dan başlayarak numaralandırılırlar. Satırdaki sayılar komşu sütunlarının boşluklarına gelir ve bu basit yapı tüm üçgen boyunca sürer. 0. satıra yalnızca 1 değeri yazılır. Sonraki satırlar oluşturulurken, hesaplanan noktanın sol üstünde ve sağ üstünde bulunan değerler çıkarılır. Eğer sağ ve sol üstünde sayı yoksa buradaki değer 1 olarak alınır. Örneğin, ilk satırın ilk sayısı 0 + 1 = 1'dir üçüncü satırda ise 4 ve 3 toplanarak 4. satırdaki 7 sayısını oluşturur.
Pascal kuralındaki binom katsayılarıyla ilişkili yapı aşağıdaki şekildeyse,
buradan
- olur.
Burada n negatif olmayan tam sayı ve k 0 ile n arasında bir tam sayıdır.
Pascal üçgeninin çok boyutlu şekilleri de vardır. 3 boyutlu olan şekli Pascal piramidi veya Paskal dörtyüzlüsü olarak anılırken diğer genel şekilli olanları Pascal basitleştirilmişleri olarak anılır.

Pascal'ın bu üçgeni, olasılıklar kuramında da ustalıkla kullanılır. Bu üçgen, biyolojideki uygulamalar, matematik, istatistik ve pek çok modern fizik konularında uygulama alanı bulur. (Bazı kaynaklara göre eski Çinliler de üçgeni tanımışlar; bazıları da Pascal üçgeni diye aslında bir Hayyam üçgeninden bahsetmişlerdir.)
Olasılıklar kuramının çıkış nedeni, Pascal'a kumarbaz Chevalier de Mere tarafından önerilmesiydi. En önemli görevi de elli iki kâğıt oyunu oynuyordu. Bu ara tavla zarlarının, şekilleri aynı olan ayrı renkli bilyelerin önemi büyüktür. Buna bağlı olarak, ünlü Pascal üçgeni doğdu. Pascal'ın bu üçgeni, daha sonraki yıllarda çok kullanıldı. Özellikle seri açılımları ve binom açılımı bu yöntemle kolaylıkla bulunur.
- Formül
- , olmak üzere
- Örneğin
- Üçgen sayılar
ikinci sıradan itibaren sağdan ya da soldan üçüncü sayı üçgen sayılardır
- İkinin üsleri
pascal üçgeninin her satırı ikinin 0 dan itibaren üslerini verir
- Binom açılımı
(a-b) veya (a+b) parantezlerinin açılımının katsayılarını verir örnek:
- Yazı tura
Kaç parayla yazı tura attıysak o satırla ilgileneceğiz iki parayla yazı tura attık ikinci sıradaki sayıları toplayalım 4 çıktı ikinci sıra 1-2-1 dir birinci sıradan 2 tura 0 yazı diye sayalım iki paranın ikisinin de tura gelme şansı 1tura 1yazı gelme şansı 2yazı gelme şansı
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Pascal ucgeni matematikte binom katsayilarini iceren ucgensel bir dizidir Fransiz matematikci Blaise Pascal in soyadiyla anilsa da Pascal dan once Hindistan Iran Cin Almanya ve Italya da matematikciler tarafindan calisilmistir Pascal ucgeninin ilk alti satiri Genellikle Pascal ucgeninin satirlari ustten n 0 dan baslayarak numaralandirilir ve her satirdaki sayilar ise soldan itibaren k 0 dan baslayarak numaralandirilirlar Satirdaki sayilar komsu sutunlarinin bosluklarina gelir ve bu basit yapi tum ucgen boyunca surer 0 satira yalnizca 1 degeri yazilir Sonraki satirlar olusturulurken hesaplanan noktanin sol ustunde ve sag ustunde bulunan degerler cikarilir Eger sag ve sol ustunde sayi yoksa buradaki deger 1 olarak alinir Ornegin ilk satirin ilk sayisi 0 1 1 dir ucuncu satirda ise 4 ve 3 toplanarak 4 satirdaki 7 sayisini olusturur Pascal kuralindaki binom katsayilariyla iliskili yapi asagidaki sekildeyse x y n k 0n nk xn kyk displaystyle x y n sum k 0 n n choose k x n k y k buradan nk n 1k 1 n 1k displaystyle n choose k n 1 choose k 1 n 1 choose k olur Burada n negatif olmayan tam sayi ve k 0 ile n arasinda bir tam sayidir Pascal ucgeninin cok boyutlu sekilleri de vardir 3 boyutlu olan sekli Pascal piramidi veya Paskal dortyuzlusu olarak anilirken diger genel sekilli olanlari Pascal basitlestirilmisleri olarak anilir Ucgendeki her sayi ust taraftaki iki sayinin toplanmasiyla elde ediliyor Pascal in bu ucgeni olasiliklar kuraminda da ustalikla kullanilir Bu ucgen biyolojideki uygulamalar matematik istatistik ve pek cok modern fizik konularinda uygulama alani bulur Bazi kaynaklara gore eski Cinliler de ucgeni tanimislar bazilari da Pascal ucgeni diye aslinda bir Hayyam ucgeninden bahsetmislerdir Olasiliklar kuraminin cikis nedeni Pascal a kumarbaz Chevalier de Mere tarafindan onerilmesiydi En onemli gorevi de elli iki kagit oyunu oynuyordu Bu ara tavla zarlarinin sekilleri ayni olan ayri renkli bilyelerin onemi buyuktur Buna bagli olarak unlu Pascal ucgeni dogdu Pascal in bu ucgeni daha sonraki yillarda cok kullanildi Ozellikle seri acilimlari ve binom acilimi bu yontemle kolaylikla bulunur Formul nk n k n k n1 n 12 n k 1k displaystyle n choose k frac n k cdot n k frac n 1 cdot frac n 1 2 cdot ldots cdot frac n k 1 k n k N0 displaystyle n k in mathbb N 0 olmak uzereOrnegin 53 5 3 2 5 4 3 2 3 5 42 202 10 displaystyle 5 choose 3 frac 5 3 cdot 2 frac 5 cdot 4 cdot 3 2 cdot 3 frac 5 cdot 4 2 frac 20 2 10 Ucgen sayilar ikinci siradan itibaren sagdan ya da soldan ucuncu sayi ucgen sayilardir Ikinin usleri pascal ucgeninin her satiri ikinin 0 dan itibaren uslerini verir Binom acilimi a b veya a b parantezlerinin aciliminin katsayilarini verir ornek a b 2 a2 2ab b2 displaystyle a b 2 a 2 2ab b 2 a b 2 a2 2ab b2 displaystyle a b 2 a 2 2ab b 2 Yazi tura Kac parayla yazi tura attiysak o satirla ilgilenecegiz iki parayla yazi tura attik ikinci siradaki sayilari toplayalim 4 cikti ikinci sira 1 2 1 dir birinci siradan 2 tura 0 yazi diye sayalim iki paranin ikisinin de tura gelme sansi14 displaystyle 1 over 4 1tura 1yazi gelme sansi 12 displaystyle 1 over 2 2yazi gelme sansi 14 displaystyle 1 over 4
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State