Matematikteki Poincaré yinelenme teoremine göre, dinamikleri hacmini koruyan ve sınırlı mekansal hacimle sınırlanan bir sistem, yeterli süre sonra, baştaki durumuyla aynı olacak veya ona çok yakın bir biçimde yinelenecektir.
Teorem adını, 1890 yılında geliştiren Henri Poincaré'den alır.
Kesin Formülasyon
Sıradan bir diferansiyel denklem tarafından tanımlanan herhangi bir dinamik sistem, kendi üzerinde faz uzayını haritalayan bir akış haritası belirler. Faz uzayındaki bir kümenin hacmi akış altında değişmez ise sistemin hacim koruyucu olduğu söylenir. Örneğin, tüm Hamilton sistemleri Liouville teoremi nedeniyle hacim koruyucudur. O halde teorem şudur: Eğer akış hacmi koruyorsa ve sadece sınırlı yörüngelere sahipse, bulunan her açık kümesi için o kümeyle sonsuz sıklıkta kesişen bir küme daha vardır.
Kuantum mekaniksel versiyon
Ayrık enerji öz durumlu zamandan bağımsız kuantum mekanik sistemler için benzer bir teorem geçerlidir. Her biri için 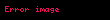


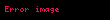
İspatın temel unsurları aşağıdaki gibidir. Sistem zamanla şunlara göre gelişir:
burada 



Toplamı T'den bağımsız bir n = N de kesebiliriz, çünkü

N'yi artırarak keyfi olarak küçük yapılabilir; 
Sonlu toplam
aşağıdaki yapıya göre, t zamanının belirli seçimleri için keyfi olarak küçük yapılabilir. Keyfi bir seçim yapın 

,
tüm sayılar için 
bu nedenle,
.
Durum vektörü 

Ayrıca bakınız
Kaynakça
- ^ Barreira, Luis (2006). Zambrini, Jean-Claude (Ed.). Poincaré recurrence: Old and new. XIVth International Congress on Mathematical Physics. World Scientific. ss. 415-422. doi:10.1142/9789812704016_0039. ISBN .
- ^ Bocchieri, P.; Loinger, A. (1957). "Quantum Recurrence Theorem". Phys. Rev. 107 (2): 337-338. Bibcode:1957PhRv..107..337B. doi:10.1103/PhysRev.107.337.
- ^ Percival, I.C. (1961). "Almost Periodicity and the Quantal H theorem". 2 (2): 235-239. Bibcode:1961JMP.....2..235P. doi:10.1063/1.1703705.
- ^ Schulman, L. S. (1978). "Note on the quantum recurrence theorem". Phys. Rev. A. 18 (5): 2379-2380. Bibcode:1978PhRvA..18.2379S. doi:10.1103/PhysRevA.18.2379.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikteki Poincare yinelenme teoremine gore dinamikleri hacmini koruyan ve sinirli mekansal hacimle sinirlanan bir sistem yeterli sure sonra bastaki durumuyla ayni olacak veya ona cok yakin bir bicimde yinelenecektir Teorem adini 1890 yilinda gelistiren Henri Poincare den alir Kesin FormulasyonSiradan bir diferansiyel denklem tarafindan tanimlanan herhangi bir dinamik sistem kendi uzerinde faz uzayini haritalayan bir akis haritasi belirler Faz uzayindaki bir kumenin hacmi akis altinda degismez ise sistemin hacim koruyucu oldugu soylenir Ornegin tum Hamilton sistemleri Liouville teoremi nedeniyle hacim koruyucudur O halde teorem sudur Eger akis hacmi koruyorsa ve sadece sinirli yorungelere sahipse bulunan her acik kumesi icin o kumeyle sonsuz siklikta kesisen bir kume daha vardir Kuantum mekaniksel versiyonAyrik enerji oz durumlu zamandan bagimsiz kuantum mekanik sistemler icin benzer bir teorem gecerlidir Her biri icin e gt 0 displaystyle varepsilon gt 0 and T0 gt 0 displaystyle T 0 gt 0 T den daha buyuk bir zaman vardir T0 displaystyle T 0 oyle ki ps T ps 0 lt e displaystyle psi T rangle psi 0 rangle lt varepsilon nerede ps t displaystyle psi t rangle t aninda sistemin durum vektorunu gosterir Ispatin temel unsurlari asagidaki gibidir Sistem zamanla sunlara gore gelisir ps t n 0 cnexp iEnt ϕn displaystyle psi t rangle sum n 0 infty c n exp iE n t phi n rangle burada En displaystyle E n enerji oz degerleri dogal birimleri kullaniyoruz bu nedenle ℏ 1 displaystyle hbar 1 ve ϕn displaystyle phi n rangle enerji oz durumlaridir Zamandaki durum vektorunun farkinin Kare normu T displaystyle T ve zaman sifir olarak yazilabilir ps T ps 0 2 2 n 0 cn 2 1 cos EnT displaystyle psi T rangle psi 0 rangle 2 2 sum n 0 infty c n 2 1 cos E n T Toplami T den bagimsiz bir n N de kesebiliriz cunku n N 1 cn 2 1 cos EnT 2 n N 1 cn 2 displaystyle sum n N 1 infty c n 2 1 cos E n T leq 2 sum n N 1 infty c n 2 N yi artirarak keyfi olarak kucuk yapilabilir n 0 cn 2 displaystyle sum n 0 infty c n 2 baslangic durumunun kare normu olan 1 e yakinsar Sonlu toplam n 0N cn 2 1 cos EnT displaystyle sum n 0 N c n 2 1 cos E n T asagidaki yapiya gore t zamaninin belirli secimleri icin keyfi olarak kucuk yapilabilir Keyfi bir secim yapin d gt 0 displaystyle delta gt 0 ve sonra tam sayilar olacak sekilde T yi secin kn displaystyle k n bu tatmin edici EnT 2pkn lt d displaystyle E n T 2 pi k n lt delta tum sayilar icin 0 n N displaystyle 0 leq n leq N Bu ozel secim icin T 1 cos EnT lt d22 displaystyle 1 cos E n T lt frac delta 2 2 bu nedenle 2 n 0N cn 2 1 cos EnT lt d2 n 0N cn 2 lt d2 displaystyle 2 sum n 0 N c n 2 1 cos E n T lt delta 2 sum n 0 N c n 2 lt delta 2 Durum vektoru ps T displaystyle psi T rangle boylece keyfi olarak baslangic durumuna yakin bir sekilde dondurur ps 0 displaystyle psi 0 rangle Ayrica bakinizBoltzmann beyni Ergodik kuramiKaynakca Barreira Luis 2006 Zambrini Jean Claude Ed Poincare recurrence Old and new XIVth International Congress on Mathematical Physics World Scientific ss 415 422 doi 10 1142 9789812704016 0039 ISBN 978 981 256 201 2 Bocchieri P Loinger A 1957 Quantum Recurrence Theorem Phys Rev 107 2 337 338 Bibcode 1957PhRv 107 337B doi 10 1103 PhysRev 107 337 Percival I C 1961 Almost Periodicity and the Quantal H theorem 2 2 235 239 Bibcode 1961JMP 2 235P doi 10 1063 1 1703705 Schulman L S 1978 Note on the quantum recurrence theorem Phys Rev A 18 5 2379 2380 Bibcode 1978PhRvA 18 2379S doi 10 1103 PhysRevA 18 2379
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State