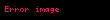Bu sayfa dinamik sistemlere dair genel bakış açılarını içerir ayrıntılı bilgi için veya çalışmak amaçlı dinamik sistemler teorisine bakabilirsiniz.

Dinamik sistem, geometrik uzay katmanındaki bir noktanın zamana bağlı durumunu tarif eder. Sarkaçlı bir saatin sarkacının salınımını, bir borudan geçen suyun hareketini ve her ilkbaharda bir göldeki balık sayısını (n değişimini/miktarını) anlatan matematiksel modeller buna bir örnektir.
Dinamik bir sistemin herhangi bir zaman aralığında/anında, reel sayılar ile (vektör ile) gösterilen bir konumu vardır, bu konum uzayda (çok katlı uzayda) uygun bir noktayla gösterilebilir. Sistemin durumunda meydana gelen ufak değişikliklere onu temsil eden rakamların değişikliği eşlik eder. Dinamik sistemlerdeki gelişim kanunu, dinamik bir sistemin şu anki durumunun gelecekteki geçireceği değişimleri açıklayan bir (şu anki durumun fonksiyonu) fonksiyonudur. Bu prensip rastgele sonuçlar üretmez, diğer bir deyişle sistemin şu anki durumunu takip edecek sadece tek bir gelecek durum vardır.
Genel Bakış
Dinamik sistem orijinini klasik mekanik (Newton mekaniğinden) alır. Diğer doğa bilimleri ve mühendislik disiplinleri gibi, bir sistemin sadece kısa bir zaman sonraki durumunu bildiren gelişim kuralının, sistemle, kapalı bir ilişkisi vardır (bkz (bu ilişki diferansiyel denklem, yineleme ilişkisini açıklayan ya da zaman -ölçek kalkulüsü-bkz time-scale calculus- gibi bağlamlardan herhangi biri olabilir). Sistemin gelecekteki tüm zamanlar boyunca durumunu gösterebilmek için bu hesaplama sürecinin, ölçülebilen her en düşük zaman aralığı için, tekrarlanması gerekir. Bu tekrarlama prosedürü sistemi analiz etmek/çözmek ya da integral hesabını (integral hesabında birim ölçütler toplanır özetle, ayrıntılı bilgi için integral) yapmak olarak da adlandırılabilir. Eğer sistem bu hesaplamalarla çözülebiliyorsa, verilen herhangi bir durum-zaman için bu sistemin gelecekteki durumları hesaplanabilir ve zaman boyunca sistemin durumunu simgeleyen bu noktalar orbit (yörünge, bir fonksiyonun grafiğinin noktalarla çizilmesi gibi) meydana getirir.
Bilgisayarların kullanımından önce, bu yörüngeyi bulmak oldukça kompleks matematiksel işlemler gerektiriyordu ve sadece sınırlı sayıda dinamik sistem için çözüm üretilebiliyordu. Sayısal yöntemleri kullanabilen elektronik hesaplama makineleri dinamik sistemlerin yörüngelerini belirleme hesaplamalarını basitleştirdi.
Basit dinamik sistemler için, yörüngesini bilmek yeterliydi ancak pek çok dinamik sistem sadece yörüngesiyle analiz edilemeyecek kadar komplekstir. Yörüngelerin bilinmesinin yetersiz kalmasının sebepleri:
- Çalışılan sistem sadece yaklaşık olarak ifade ediliyor olabilir; bu sistemin parametreleri kesin olarak bilinmiyor olabilir ya da bu sistemi ifade eden denklem çözülürken bazı terimler tam olarak hesaba katılamıyor olabilir. Sistemin yaklaşımlarla ifade edilmesi, bizi kullanılan yöntemlerin uygun ya da genel geçer olup olmadığı sorusuna yönlendirir. Bu tür sorulara cevaben uygulanan yöntemlerin isabetliliğini gösteren birkaç yöntem geliştirilmiştir, ve (ayrıntılı bilgi için bkz, Lyapunov stability ve structural stability). Dinamik sistemin denkliği ya da kararlılığı, yörüngelerin ile verilen ilk pozisyonu arasındaki eşitliğin kurulabileceğinin göstergesidir. Yörüngelerin sistemle eşitliğini göstermek için kullanılacak denklik kavramları değiştikçe eşitlik hesapları da değişir.
- Yörüngenin ne tür olduğu daha önemli olabilir.Bazı yörüngeler, diğer yörüngeler sistemin farklı durumlarını gösteren farklı eğriler/doğrularken, periyodik olabilir. Genelde, hesaplamalar için bu farklı eğriler numaralandırılır (farklı sınıflara ayrılır) ya da tek bir sınıf altında toplanır. Tüm bu yörüngeleri sınıflandırma çalışmaları, bizi dinamik sistemler üstüne niteliksel bir çalışmaya götürür, koordinat değişiklikleriyle değişmeyen özelliklerin araştırılmasına. ve , sınıflandırılmış yörüngelerinden anlaşılmış dinamik sistemlere birer örnektir.
- Yörüngelerin davranışının (yönelişleri, eğimleri vb.) bir parametreye göre fonksiyonu bir uygulama için gerekli olan durumlar. Bir parametre değiştiğinde, dinamik sistemin davranışının değiştiğini işaret eden, dinamik sistemin yörüngesi çatallanabilir/yörüngeler ayrılabilir (bkz ayrım noktaları, ). Örneğin; sadece periyodik bir yol izlerken bir anda rastgele bir yol izleyebilir (sıvının türbülansında olduğu gibi).
- Yörüngeler tamamen rastgele olabilir. Bu durumda en uzun yörüngeyi veya birden çok (fraklı davranan) yörüngeyi kullanarak ortalamanın alınması gerekebilir. Ergodik sistemler için ortalamalar oldukça iyi tanımlanmıştır (daha fazla bilgi için bkz Ergodik teori) ve daha detaylı olan hiperbolik sistemler içinde ortalama hesaplamaları ortaya konmuştur (bkz ). Dinamik sistemlerin olasılıklı halleri üstünde çalışmaların kazandırdığı kavrayış, istatistiksel mekanik ve kaos teorisinin temellerinin atılmasını sağlamıştır.
Tarihçe
Pek çok kişi dinamik sistemlerin kurucusu olarak Henri Poincaré'yi görür. Poincaré, "New Methods of Celestial Mechanics" (gök mekaniğinde yeni yöntemler) (1892–1899) ve "Lectures on Celestial Mechanics" (gök mekaniği üstüne dersler) (1905–1910) isimli iki adet monografi yayınladı. Bu kitaplarda üçlü sistemler (hareketleri) üstündeki çalışmalarının sonucunda elde ettiği yöntemleri hatasız bir şekilde uyguladı ve çözümleri üstünde daha detaylı çalışmalar yaptı (frekansları, yörüngelerin denklikleri, asimptotları vb.). Bu kağıtlardaki çalışmalara göre. (Poincare'in yineleme teorisini de içeriyorlardı) Herhangi bir sistem yeterli bir zaman geçtikten sonra, yeterli ancak ölçülebilir zaman, ölçümün başladığı o ilk pozisyonuna çok yakın bir yere dönüyordu.
Aleksandr Lyapunov pek çok, önemli, yaklaşım yöntemleri geliştirdi. 1899 yılında geliştirdiği bu yöntemleri,adi diferansiyel denklem kümelerinin kararlığının hesaplanmasını mümkün kılıyordu. Dinamik sistemler için modern kararlılık teorisini üretmiştir.
1913 yılında, George David Birkhoff'un Poincaré'nin ",üçlü sistemdeki özel bir durum için, kanıtlaması ismini dünyaya tanıttı. 1927 yılında, şimdi olarak bilinen ve ortaya atmış olduğu en uzun ömürlü çalışması olan Dynamical Systems22 Nisan 2006 tarihinde Wayback Machine sitesinde . i yayınladı. Ergodik hipotezden edilmiş fiziksel sezinin ve matematiksel hesaplamayla kombine olması, en azından prensipte, istatistiksel mekaniğin temel sorununun çözümünü oluşturuyordu. Ergodik teori aynı zamanda dinamikten esinlenmeler de içerir.
'in de büyük katkıları olmuştur. İlk katkısı at nalı haritası (ayrıntılı bilgi için bkz ) ile dinamik sistemlerde kayda değer çalışmalar yapmıştır. Ayrıca başkalarının pek çok kez baş vurduğu bir araştırma programı da yapmıştır.
1964 yılında , kesintili (bkz discrete dynamical system) dinamik sistemlerin periyotları üstünde çalışması sonucu geliştirmiştir. Teoremin çıkarımlarından birine göre, sayı doğrusundaki, kesintili bir dinamik sistem eğer üç adet periyot noktası barındırıyorsa diğer her periyotlarda da periyodik nokta bulundurmak zorundadır.
Temel tanımlar
Dinamik bir sistem çok katlı bir uzay (lineer uzanan, M diye adlandırılan, gelişim/evrilen fonksiyonlar Φt kümesini içeren uzay) katmanındaki noktanın tekrar o katmana (t geçen zamanı ifade ederken, t ∈ T) dönüşünü gösteren bir harita olarak düşünülebilir. Fonksiyonlardaki lineerlik kavramı, kullanılan uygulamalara ve çok katlıların tiplerine göre değişiklik gösterir. T kümeleri için birden fazla seçim olanağı olabilir. T gerçek sayılar kümesi olarak alındığında, dinamik sistem akışkan olarak nitelenebilir (bkz ); eğer T sadece pozitif gerçek sayılar kümesi olarak alındığında, dinamik sistem yarı akışkan olarak nitelenir. T tam sayı kümesi olarak alındığında kaskat (cascade, şelale, ardışık kelimelerine karşılık gelir) ya da bir plan, sadece pozitif tam sayılar olarak alınırsa yarı kaskat olarak nitelendirilebilir.
Örnekler
Φt ile gösterilen gelişim fonksiyonu genelde hareket için yazılmış diferansiyel denklemin bir çözümüdür;
Bu denklem, faz uzayında, x0 (herhangi bir ilk konum demektir)dan başlayıp x(t)'yi izleyen yörüngenin zamanının türevini verir (üstünde noktayla gösterilmiş, türev). v(x) ile gösterilen vektör alanı, Min bu alanın her noktasında (faz uzayının her noktasında) dinamik sistem için hız vektörünü oluşturduğu lineer bir fonksiyondur (Tabii ki, bu hız vektörleri M faz uzayında/uzay katmanındaki herhangi bir vektör değil herhangi bir x noktası için TxM ile gösterilen eğim uzayında bulunan vektörlerdir-eğim uzayından kasıt, eğimi oluşturan ögelerin meydana getirdiği uzaydır-). Verilen Φt lineer fonksiyonundan otonom bir vektör alanı türetilebilir.
v(x) için ne yüksek dereceli türevlere ne de zaman parametresini kullanmaya gerek vardır çünkü bu çokluklar sistemleri çok boyutlu uzayda açıkladığımız zaman ortadan kalkarlar. Adi diferansiyel denklemlerin dışında kalan diğer diferansiyel denklem türleri de gelişim kuralını ifade etmek için kullanılabilir:
denklemi kompleks karışıklıklardan dolayı ifade edilmesi güçleşen mekanik bir sistemin farklı bir gösterimine örnektir.
Φt gelişim fonksiyonunu anlatmak için genelde adi diferansiyel denklemler kullanılır, bu durumda M, sonlu olan, çok katlı uzay boyutunu gösterir.Dinamik sistemlerdeki pek çok kavram, sonsuz katmanlı uzaylara dek genişletilebilir. Örnek: -ayrıntılı bilgi için bkz banach sapaces- tabii bu durumda kısmi diferansiyel denklemler kullanılır. Yirminci yüzyılın sonlarında dinamik sistemlere kısmi diferansiyel kullanarak yaklaşmak oldukça yaygın bir kullanım olmuştu.
İleri düzey örnekler(ayrıntılı bilgi için orijinal isimlerine bakabilirsiniz)
- ,Bifurkasyon
- ,
- ,
- ,
- ,
- ,
- is an example of a chaotic map
- and
- ,
- ,
Lineer dinamik sistemler
Lineer dinamik sistemler basit fonksiyonlar ya da sınıflandırılmış yörüngeler kullanılarak rahatlıkla ifade edilebilen dinamik sistemler sınıfıdır. N boyutlu Öklid uzayındaki uzay katmanları (nın herhangi biri) N tane vektör ile gösterilebilir. Lineer sistemler üstünde çalışmak mümkündür çünkü, çakışma prensibine uyarlar; eğer u(t) ve w(t) vektör alanı için olan diferansiyel denklemi sağlarlarsa (ilk konumu sağlamaları şart değildir) bunların toplamı da sağlar u(t)+w(t).
Akışlar
Bir akış için(sıvının akışı) Φ(x) vektör alanı, uzay katmanındaki bir konum için, afin fonksiyonudur,
bu denklemde A matris, b sayıların oluşturduğu vektör, x ise konum vektörüne karşılık gelir.Bu sistem çakışma prensibi(lineerlik) kullanılarak çözülebilir.
b ≠ 0 with A = 0 olması durumunda bu denklem b yönündeki bir doğru denklemidir.
b sıfır ve A≠0 iken, orijin akıştaki bir denge noktasıdır ve eğer x0= 0 ise yörünge sabit kalır.Bundan farklı ilk konumlar için bu hareket denklemi; matrisin, x0 ilk konumu için, üslü fonksiyonu kullanılarak oluşturulabilir.
b = 0 iken, Anın uzay katmanının yapısını belirler. Anın eigen değerleri ve kullanılarak ilk konumun denge noktasına doğru yaklaşacağı ya da uzaklaşacağını hesaplamak mümkündür.
A ≠ 0 olduğu durumlarda iki farklı ilk konum arasındaki mesafe üssel olarak değişir, ya üssel olarak yaklaşır ya da üssel olarak uzaklaşırlar. Lineer sistemler, yaklaşma durumlarında, ilk konumlara oldukça hassas bir şekilde bağlıdırlar (ufak değişiklikler bile sonuçları değiştirir). Lineer olmayan sistemlerde bu (gerekli ancak yine de yeterli gelmeyen) kaotik teori için de gerekli şartlardandır.
Haritalar
, dinamik sistemleri matris diferansiyel denklemi ile gösterilir (ayrıntılı bilgi için bkz;):
A bir matrisi,b ise bir vektörü gösteriyor.Devamlı olan durumlarda,koordinatların dğişimi x → x + (1 − A) –1b denklemdeki b yi ortadan kaldırır.Yeni koordinat sisteminde,orijin haritada belli bir noktadadır ve lineer sistemin çözümleri;A nx0 ile gösterilir. haritanın çözümleri artık eğrilerle değil,uzay katmanlarından atlayan noktalarla gösterilir.Yörüngeler(haritanın üstündeki noktalar toplamının oluşturduğu),eğriler veya lifler şeklinde düzenlenir.
Devamlı olan durumlarda(devamlı fonksiyon gibi)olduğu gibi, Anın eigen değerleri ve vektörleri uzay katmanının yapısını belirler.Örneğin, u1Anın eigen vektörü olsun,birden küçük eigen değeri için,α u1 noktalarından geçen doğrular(α ∈ R) haritadaki sabit eğrilerdir.Bu doğrudaki noktalar sabit değerlerdir.
Kesintili dinamik sistemlere daha çok örnek için bkz(,).
Yerel dinamikler
Dinamik sistemlerin niteliksel özellikleri koordinatlarda lineer değişimler olsa bile değişmez(bu açıklama bazen nitelik kavramının tanımı olarak görülür):vektör alanındaki yalnız bir nokta(v(x) = 0 olduğu nokta)lineer değişimler sonucu yine tek bir nokta olarak kalacaktır;periyodik yörünge,uzay katmanındaki bir döngü/düğümdür ve bu uzay katmanındaki lineer dönüşümler sonucu yine aynı döngü olarak kalacaktır.Dinamik sistemlerde uzay katmanındaki tek noktalar ve döngüsel yörüngelerin yakınları yeterince iyi anlaşılabilmektedir.Dinamik sistemler üstündeki kapsamlı çalışmalar gösteriyor ki;koordinatlardaki değişimi(değişimler spesifik olarak bilinmese de hesaplanabilir olduğu zaman) kullanarak dinamik sistemlerin analizleri çok daha kolay oluyor.
Düzenleme,idealleştirme
Uzay katmanının küçük parçacıklarının akışı çok basit formlara indirgenebilir.Eğer y v(y) ≠ 0 denkliğini sağlayan bir noktaysa,o halde ynin çevresindeki vektör alanının birbirine paralel ve aynı büyüklükte geçen vektörler olmasını sağlayacak bir koordinat değişikliği yapılabilir (bu değişiklik vardır).Bu düzenleme teoremi olarak bilinir.
Düzenleme teoremi der ki;tek noktalardan uzaktaki bir paketin içindeki noktanın dinamikleri bir doğruyu meydana getirir.Bu paket bazen başka paketlerle birleşerek büyüyebilir,ve bu çözüldüğünde,tüm uzay katmanı M için uzay integrallenebilirdir.Çoğu durumda bu paket tüm uzay katmanını dolduramaz.Vektör alanında tek noktalar olabilir (v(x) = 0 olduğunda)veya paketler bir noktaya yaklaşırken git gide küçülebilir.Bu genelin doldurulamayışı için daha sağlam bir neden,yörüngelerin paketten çıktıktan sonra(belki diğer paketlere uğradıktan sonra) yine aynı yerine dönmesi olabilir.Eğer yörünge bir döngüye girerse,bu vektör alanını düzenlemek tüm paketler için düzenlemek imkânsız olur.
periyodik yörüngelerin komşulukları
Genel olarak,periyodik bir yörüngenin çevresi için düzenleme teoremi kullanılamaz.Poincaré periyodik yörüngenin yakınlarının üstünde hesaplama yapılabilmesi için bir dönüşüm formülü geliştirdi .γ yörüngesinde bir x0 noktası seçin ve uzay katmanındaki o noktaya yakın noktaların v ye dik olduğunu görün(x0 iken). Bu noktalara,S(γ, x0) Pontcare kesiti(ayrıntılı bilgi için bkz,) denir.Şimdi akış bir haritayı gösteriyor, F : S → S,Sden başlayıp Se dönen noktalar için.Her noktanın dönmesi için farklı farklı zamanlar geçecektir ancak geçen zamanlar ilk konumdan başlayana yakın olacaktır (x0).
Periyodik yörünge ile Poincare kesitinin kesiştiği nokta Poincare haritasında belirli bir noktaya karşılık gelir (F).Doğrusal yer değiştirme sonucu bu noktanın x = 0 a denk geleceği var sayılabilir.Haritanın Taylor serileri ile gösterilişi;F(x) = J • x + O(x2), yani koordinatlardaki bir değişikliğin,h,sadece Fnin lineer kısmının basitleşmesine neden olacağı tahmin edilebilir;
Bu birleşim denklemi olarak bilinir.Bu denklemin geçerli olduğu koşulların bulunması,dinamik sistemler üstündeki araştırmalarda en önemli önceliklerden biri olmuştur.Poincaré ilk olarak tüm fonksiyonların analiz edilebilir olduğunu varsayarak yaklaşmış ve rezonans olmama koşulunu keşfetmiştir.Eğerλ1, ..., λν sayıları J nin eigen değerleriyse,ve eigen değerlerinden biri lineer olarak(iki veya daha fazlasının)kombine edilmiş haliyse bu sayılar birbirinin rezonansı olmalıdır.λi – ∑ terimleri (diğer eigen değerlerinin katları)h fonksiyonunda payda da yer alırsa,rezonans olmama koşulu aynı zamanda küçük bölen problemi olarak da bilinir.
Birleşim/girişim Sonuçları
Birleşim denkleminin sonuçları olabilmesi,Jnin eigen değerlerine ve hnin derecesinin bir olmasına bağlıdır (lineer olması için).Jnin herhangi özel bir simetriye sahip olmasına gerek olmadığından,Jnin eigen değerleri karmaşık sayılar olabilir.jnin eigen değerleri birim çember üzerinde olmadığında,F üstündeki sabit x0 noktaları sabit hiperbolik noktalar olarak adlandırılır ve eigen değerleri çember üzerinde olmasının yanı sıra karmaşık sayılar olurlarsa eliptik olarak adlandırılır.
Hiperbolik olduğu durumda, lineer haritadaki sabit J • x noktasının komşuluğunun devamlı olduğu fonksiyonu verecek olan şartları ortaya koyar.Hiperbolik durum aynı zamanda yapısal kararlılığa da sahiptir.Vektör alanındaki küçük değişiklikler Poincare haritasında sadece küçük değişiklikler yaratacak ve bu küçük değişiklikler Jnin eigen değerlerinde ufak değişiklikleri meydana getirecek(karmaşık sayılar düzleminde) ki bu yeni eigen değerlerinin görünümü yine hiperbolik bir şekle sahip olacak.
teoremi eliptik noktanın komşuluğunun davranışını açıklar.
Bifurkasyon(çatallanma) teorisi
Gelişim haritası(ya da ondan türetilen vektör alanı) Φt μ gibi bir parametreye bağlı olduğu zaman uzay katmanının yapısı da bu parametreye bağlı olur.Belli bir μ0 değerine ulaşmadan,bu parametredeki değişimler uzay katmanında bir değişiklik yaratmazlar.O nokta aşıldıktan sonra uzay katmanı ölçülebilir bir şekilde değişir (değişim gözlemlenecek bir şekilde) ve dinamik sistemde bir çatallanma meydana gelir.
Bifurkasyon teorisi,uzay katmanının yapısı(özellikle sabit noktalar(bakz,periyodik yörüngeler ya da sabit yumrular(bkztorus için)ve μ parametresi için davranışını/değişimini inceler.Çatallanma noktasında,yapı kararlılığını değiştirebilir,yeni yapılar oluşturmak üzere bölünebilir ya da diğer yapılarla birleşebilir.Taylor serileriyle yaklaşımları kullanarak ve koordinat değişikliği nedeniyle eksik kalan(yok olan) parametreleri anlayarak dinamik sistemlerdeki çatallanmaları sınıflandırmak mümkün olabilir.
Fμ ailesine ait bir hiperboliğin x0 noktasındaki çatallanmaları DFμ(x0) ile sistemin çatallanma noktasındaki ilk türevi alınarak hesaplanabilir.Haritada,DFμnin eigen değerlerinin bir çember üstünde olması orada çatallanma olacağını gösterir.Bir akışta eigen değerleri sanal eksen üstünde olduğunda çatallanma olur.Daha fazla bilgi için bkz
Bazı çatallanmalar uzay katmanında oldukça karışık yapıların meydana çıkmasına sebep olurlar.Öreğin; periyodik bir çatallanmanın bit yumruya,yumrunun da oldukça karmaşık bir çekiciye dönmesini anlatır (ayrıntılı bilgi için bkz,).Başka bir örnekle, sabit bir periyodik yörüngenin çifter periyodik çatallanmalara ayrıldıını anlatır (ayrıntılı bilgi çin bkz,).
Ergodik sistemler
Pek çok dinamik sistemde,hacmin(v boyutlu bir hacim) uzay katmanından bağımsız olacağı bir koordinat ekseni seçmek mümkündür.Bu Newton'un kanunlarına dayandırılarak üretilmiş sistemlerde mümkündür(kooridantlar konum ve momentum olacak şekilde bir koordinatlar ekseni,ve hacmin birimi(konum) × (momentum) birimleri cinsinden belirtildikçe).Akışta A kümesinden bir alt küme Φ t(A) fonksiyonuyla işleme sokulur ve uzay katmanından bağımsızlı şu denklikle gösterilir;
Hamilton mekaniğinde koordinatlar bilindikçe genel(çalışmalar için elverişli)bir momentum değeri,hacimden(akış sırasında hacmin korunan sistemler için) bulunabilir.Hacmin ile bulunabilir (ayrıntılı bilgi için bkz,).
Bir Hamilton sisteminde,her çeşit kozum-momentum değerini bulmak(ilk şartlar bilindiği takdirde) mümkün değildir.Çünkü enerji korunumu sadece ilk şartlardaki enerji miktarı ile eşit olan durumlar için uygulanabilirdir. Ω adlı enerji kabuğundaki enerji miktarıyla aynı olan enerjiler o uzay katmanının alt kümeleridirler.Enerji katmanının hacmi Liouville hesabıyla bulunur ve gelişim şartları altında korunurdur.
Akışlarda hacimleri korunan sistemlerde,Poincaré,Poincaré yineleme teorisini ortaya koydu.Bu teoreme göre;bir uzay katmanının sonlu bir Liouville hacmine sahip olduğunu ve Fnin hacim korunumlu bir uzay katmanı haritası ve Anın da uzay katmanının alt kümesi olduğunu var sayın.O halde (neredeyse)her bir A noktası tekrar A noktasına sonsuz sıklıkta döner.Poincaré'nin yineleme teorisi tarafından 'nın çarpışan atomların oluşturduğu dinamik sisteminden entropinin arttığı yönündeki çıkarımına itiraz etmek için kullanıldı.
Boltzmann'ın çalışmasına yöneltilen sorulardan biri,ortalama zaman ve ortalama uzayın arasındaki eşitlik olma ihtimaliyle ilgiliydi(ergodik hipotez olarak adlandırdığı).Hipoteze göre zamanın uzunluğu(vektörel)nun A bölgesinde katettiği miktar; vol(A)/vol(Ω) idi.
Ergodik hipotezin istatistiksel mekaniğin gelişimi için temel taş olmadığı ve ergodik benzeri diğer serilerin ilişkili fiziksel sistemlerin genel görünüşünü(çıkarım yapılabilecek görünüş)kısıtladığı ortaya atıldı. ergodik sistemlere fonksiyonel analiz kullanarak yaklaştı.a uzay katmanındaki her bir sayıyla(örneğin;ani basınç veya ortalama yükseklik) ilişkilendirilmiş olan bir fonksiyon olsun.Gözlemlenebilir değerleri başka bir zaman,gelişim fonksiyonu φ t,kullanarak ölçülebilir.Bu da bizi transfer operatörüne getirir ;U t
Lineer operatör(U)ün dağılımının özellikleri üzerinde çalışarak Φ t 'ın ergodik özelliklerini sınıflamak mümkündür.Koopman yaklaşımını kullanarak(akışın gözlemlenebilir bir fonksiyonu olduğu durumlar için),sonlu boyutlu lineer olmayan bir katman için geçerli bir problemde, Φ t fonksiyonu Uyu içeren sonlu-boyutlu bir harita ile ifade edilebilir.
Liouville hesabı,sadece enerji kabuğu(Ω)nun ortalama hesaplamları kullanıldığında geçerlidir (ayrıntılı bilgi için bkz,).Bir yönerge boyunca olan zamanın ortalamasının uzayın ortalamasının(vektörel) eşdeğer oluşu Boltzmann faktörüyle ölçülür(bkz, ).Bu fikir Sinai,Bowen ve Ruelle(SRB hesabı) gibi bilim insanları tarafından daha büyük sistem sınıfları için(korunmayan sistemlerde dahil) genellenmiştir. kaotik sistemler için Boltzmann hesabı yerine kullanılmıştır.
Lineer olamayan dinamik sistemler ve kaos
Basit lineer olmayan denklemler ve hatta parçalı lineer sistemler bazen öngörülmemiş davranışlar sergileyebilir,rastgele davranır gibi, temelde tanımlı fonksiyonlar olsalar bile.Bu rast gele gibi görünen davranış kaos olarak adlandırılır.Anosov kaotik sistemler olarak adlandırılan bu sistemlere benzer davranışlar sergileyen dinamik sistemler tanımlamıştır (yüksek kesinliklerle,ayrıntılı bilgi için bkz,).Hiperbolik sistemlerde eğim uzaylarının esas yörüngeye dik olduğu sistemler iki kısma ayrılabilir;yörüngeye yakınsak noktalar içerenler(kararlı çokkatlılar) ve yörüngeye ıraksak noktalar içeren(karasız çokkatlılar)ler.
Matematiğin bu dalı dinamik sistemlerin uzun dönem davranışlarını araştırır.Yani sadece spesifik bir kısmına odaklanmak o dinamik sistem için genel çözümler üretmemize yardımcı olmaz(bu yüzden bu dal böyle soruları sormak yerine) ancak sistem uzun bir dönem sonra kararlılık kazanacaksa bu dinginlik konumları hangi zamana denk gelir ya da uzun dönem davranışı sergileyen bu sistem kendisinin ilk şartlarından bağımsız mı hareket eder(gibi sorularla uğraşır)?
Karmaşık sistemlerin kaotik davranışından bahsetmediğimize dikkat edin.Meteoroloji karmaşık sistemler hatta kaotik davranışlar sergileyen sistemler üstüne uzun zamanlar boyunca çalışma yapmıştır.Koss teorisi hep şaşırtıcı olmuştur çünkü dikkat edilmeyen önemsiz sistemlerin dahi kaos içerdiği görülmüştür. tek ikinci derece polinom dinamik sistemdir,atnalı haritası parçalı lineer sistem bir örnektir (ayrıntılı bilgi için bkz,,).
Geometrik tanım
Dinamik sistem bir değişkenler grubudur 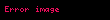

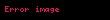
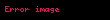
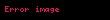
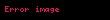
Teorik tanımın hesaplanması
Dinamik sistem formüllerle tanımlanabilir; denkliğin korunduğu dönüşümler buna bir örnek olabilir (X, Σ, μ, τ dörtlüsü kullanılarak). Diyelim ki, X bir matematiksel küme ve Σ ise X ile olan, (ayrıntılı bilgi için bkz,) sonuç olarak (X, Σ) ikilisi ölçülebilir bir uzay katanıdır. μ de sigma-cebiri ile ilişkilendirilmiş sonlu bir hesaplanma olsun ve (X, Σ, μ) üçlüsü olasılıksal uzayı oluşturur(ayrıntılı bilgi için bkz, ). Bir haritaın τ: X → X adlı ölçülebilir bir fonksiyonu sadece σ ∈ Σ nun 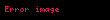
τ haritası somut bir zamana bağlı gelişimsel dinamik sistemdir.Bundan dolayı,kesintili dinamik sistemler için bu fonksiyon tekrarlanır 
Dinamik sistem örnekleri
- is an example of a chaotic piecewise linear map
- and
Çok boyutlu genelleme
Dinamik sistemler tek bir bağımsız değişken üstüne kuruludur(genelde bu değişken zamandır).Daha genel sistem sınıfları çoklu bağımsız değişkenler üstüne kuruludur ve bu yüzden çok boyutlu sistemler olarak adlandırılırlar.Bu tip sistemler matematiksel modelleme için kullanışlıdır, örneğin, görüntü işleme.
Ayrıca bakınız
Kaynakça
- ^ Strogatz, S. H. (2001). Nonlinear dynamics and chaos: with applications to physics, biology and chemistry. Perseus publishing.
- ^ Katok, A., & Hasselblatt, B. (1995). Introduction to the modern theory of dynamical systems. Cambridge, Cambridge.
- ^ Holmes, Philip. "Poincaré, celestial mechanics, dynamical-systems theory and “chaos”." Physics Reports 193.3 (1990): 137-163.
İleri düzey okulamar için
Works providing a broad coverage:
- and (1978). Foundations of mechanics. Benjamin–Cummings. ISBN . (available as a reprint: )
- Encyclopaedia of Mathematical Sciences (ISSN 0938-0396) has a sub-series on dynamical systems with reviews of current research.
- Christian Bonatti, Lorenzo J. Díaz, Marcelo Viana (2005). Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective. Springer. ISBN .
- (1967). "Differentiable dynamical systems". Bulletin of the American Mathematical Society. 73 (6). ss. 747-817. doi:10.1090/S0002-9904-1967-11798-1.
Özgün üslupları olan giriş kitapları:
- V. I. Arnold (1982). Mathematical methods of classical mechanics. Springer-Verlag. ISBN .
- and Wellington de Melo (1982). Geometric theory of dynamical systems: an introduction. Springer-Verlag. ISBN .
- David Ruelle (1989). Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. ISBN .
- Tim Bedford, Michael Keane and Caroline Series, eds. (1991). Ergodic theory, symbolic dynamics and hyperbolic spaces. Oxford University Press. ISBN .
- and (1992). Dynamics—the geometry of behavior, 2nd edition. Addison-Wesley. ISBN .
Ders kitapları:
- Kathleen T. Alligood, Tim D. Sauer and (2000). Chaos. An introduction to dynamical systems. Springer Verlag. ISBN .
- Oded Galor (2011). Discrete Dynamical Systems. Springer. ISBN .
- Anatole Katok and Boris Hasselblatt (1996). Introduction to the modern theory of dynamical systems. Cambridge. ISBN .
- Guenter Ludyk (1985). Stability of Time-variant Discrete-Time Systems. Springer. ISBN .
- Stephen Lynch (2010). Dynamical Systems with Applications using Maple 2nd Ed. Springer. ISBN .
- Stephen Lynch (2007). Dynamical Systems with Applications using Mathematica. Springer. ISBN .
- Stephen Lynch (2004). Dynamical Systems with Applications using MATLAB. Springer. ISBN .
- James Meiss (2007). Differential Dynamical Systems. SIAM. ISBN .
- Morris W. Hirsch, and Robert Devaney (2003). Differential Equations, dynamical systems, and an introduction to chaos. Academic Press. ISBN .
- Julien Clinton Sprott (2003). Chaos and time-series analysis. Oxford University Press. ISBN .
- (1994). Nonlinear dynamics and chaos: with applications to physics, biology chemistry and engineering. Addison Wesley. ISBN .
- (2012). . Providence: American Mathematical Society. ISBN . 26 Haziran 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Ocak 2015.
- Stephen Wiggins (2003). Introduction to Applied Dynamical Systems and Chaos. Springer. ISBN .
Popüler kaynaklar:
- and (1996). Celestial Encounters. Princeton. ISBN .
- (1988). Chaos: Making a New Science. Penguin. ISBN .
- (1990). Mathematics and the Unexpected (Paperback). University Of Chicago Press. ISBN .
- Ian Stewart (1997). Does God Play Dice? The New Mathematics of Chaos. Penguin. ISBN .
Dış bağlantılar
- Interactive applet for the Standard and Henon Maps13 Haziran 2011 tarihinde Wayback Machine sitesinde . by A. Luhn
- (in Monash University's Virtual Lab)
- Arxiv preprint server12 Ağustos 2013 tarihinde Wayback Machine sitesinde . has daily submissions of (non-refereed) manuscripts in Dinamik sistemler.
- DSWeb13 Ağustos 2006 tarihinde Wayback Machine sitesinde . provides up-to-date information on dynamical systems and its applications.
- Encyclopedia of dynamical systems16 Mayıs 2007 tarihinde Wayback Machine sitesinde . A part of Scholarpedia — peer reviewed and written by invited experts.
- Nonlinear Dynamics16 Ekim 2007 tarihinde Wayback Machine sitesinde .. Models of bifurcation and chaos by Elmer G. Wiens
- Oliver Knill11 Mart 2016 tarihinde Wayback Machine sitesinde . has a series of examples of dynamical systems with explanations and interactive controls.
- Sci.Nonlinear FAQ 2.0 (Sept 2003)5 Nisan 2007 tarihinde Wayback Machine sitesinde . provides definitions, explanations and resources related to nonlinear science
Çevrimiçi kitaplar ve ders notları:
- Geometrical theory of dynamical systems. Nils Berglund's lecture notes for a course at at the advanced undergraduate level.
- Dynamical systems22 Nisan 2006 tarihinde Wayback Machine sitesinde .. George D. Birkhoff's 1927 book already takes a modern approach to dynamical systems.
- Chaos: classical and quantum25 Temmuz 2011 tarihinde Wayback Machine sitesinde .. An introduction to dynamical systems from the periodic orbit point of view.
- . An introduction to the development of mathematical models of dynamic systems.
- Learning Dynamical Systems12 Temmuz 2006 tarihinde Wayback Machine sitesinde .. Tutorial on learning dynamical systems.
- Ordinary Differential Equations and Dynamical Systems26 Haziran 2012 tarihinde Wayback Machine sitesinde .. Lecture notes by
araştırma grupları:
- Dynamical Systems Group Groningen3 Nisan 2007 tarihinde Wayback Machine sitesinde ., IWI, University of Groningen.
- Chaos @ UMD12 Haziran 2005 tarihinde Wayback Machine sitesinde .. Concentrates on the applications of dynamical systems.
- , SUNY Stony Brook. Lists of conferences, researchers, and some açık sorular:
- Center for Dynamics and Geometry14 Temmuz 2014 tarihinde Wayback Machine sitesinde ., Penn State.
- Control and Dynamical Systems 30 Mayıs 2014 tarihinde Wayback Machine sitesinde ., Caltech.
- , Ecole Polytechnique Fédérale de Lausanne (EPFL).
- , University of Bremen
- , University of Oxford
- Non-Linear Dynamics Group 3 Mart 2016 tarihinde Wayback Machine sitesinde ., Instituto Superior Técnico, Technical University of Lisbon
- Dynamical Systems 2 Haziran 2017 tarihinde Wayback Machine sitesinde ., IMPA, Instituto Nacional de Matemática Pura e Applicada.
- Nonlinear Dynamics Workgroup 21 Ocak 2015 tarihinde Wayback Machine sitesinde ., Institute of Computer Science, Czech Academy of Sciences.
Simulation software based on Dynamical Systems approach:
- FyDiK20 Ocak 2009 tarihinde Wayback Machine sitesinde .
- iDMC[], simulation and dynamical analysis of nonlinear models
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu sayfa dinamik sistemlere dair genel bakis acilarini icerir ayrintili bilgi icin veya calismak amacli dinamik sistemler teorisine bakabilirsiniz The Lorenz salinimlarinda ortaya cikan dinamik sistem Dinamik sistem geometrik uzay katmanindaki bir noktanin zamana bagli durumunu tarif eder Sarkacli bir saatin sarkacinin salinimini bir borudan gecen suyun hareketini ve her ilkbaharda bir goldeki balik sayisini n degisimini miktarini anlatan matematiksel modeller buna bir ornektir Dinamik bir sistemin herhangi bir zaman araliginda aninda reel sayilar ile vektor ile gosterilen bir konumu vardir bu konum uzayda cok katli uzayda uygun bir noktayla gosterilebilir Sistemin durumunda meydana gelen ufak degisikliklere onu temsil eden rakamlarin degisikligi eslik eder Dinamik sistemlerdeki gelisim kanunu dinamik bir sistemin su anki durumunun gelecekteki gecirecegi degisimleri aciklayan bir su anki durumun fonksiyonu fonksiyonudur Bu prensip rastgele sonuclar uretmez diger bir deyisle sistemin su anki durumunu takip edecek sadece tek bir gelecek durum vardir Genel BakisDinamik sistem orijinini klasik mekanik Newton mekaniginden alir Diger doga bilimleri ve muhendislik disiplinleri gibi bir sistemin sadece kisa bir zaman sonraki durumunu bildiren gelisim kuralinin sistemle kapali bir iliskisi vardir bkz bu iliski diferansiyel denklem yineleme iliskisini aciklayan ya da zaman olcek kalkulusu bkz time scale calculus gibi baglamlardan herhangi biri olabilir Sistemin gelecekteki tum zamanlar boyunca durumunu gosterebilmek icin bu hesaplama surecinin olculebilen her en dusuk zaman araligi icin tekrarlanmasi gerekir Bu tekrarlama proseduru sistemi analiz etmek cozmek ya da integral hesabini integral hesabinda birim olcutler toplanir ozetle ayrintili bilgi icin integral yapmak olarak da adlandirilabilir Eger sistem bu hesaplamalarla cozulebiliyorsa verilen herhangi bir durum zaman icin bu sistemin gelecekteki durumlari hesaplanabilir ve zaman boyunca sistemin durumunu simgeleyen bu noktalar orbit yorunge bir fonksiyonun grafiginin noktalarla cizilmesi gibi meydana getirir Bilgisayarlarin kullanimindan once bu yorungeyi bulmak oldukca kompleks matematiksel islemler gerektiriyordu ve sadece sinirli sayida dinamik sistem icin cozum uretilebiliyordu Sayisal yontemleri kullanabilen elektronik hesaplama makineleri dinamik sistemlerin yorungelerini belirleme hesaplamalarini basitlestirdi Basit dinamik sistemler icin yorungesini bilmek yeterliydi ancak pek cok dinamik sistem sadece yorungesiyle analiz edilemeyecek kadar komplekstir Yorungelerin bilinmesinin yetersiz kalmasinin sebepleri Calisilan sistem sadece yaklasik olarak ifade ediliyor olabilir bu sistemin parametreleri kesin olarak bilinmiyor olabilir ya da bu sistemi ifade eden denklem cozulurken bazi terimler tam olarak hesaba katilamiyor olabilir Sistemin yaklasimlarla ifade edilmesi bizi kullanilan yontemlerin uygun ya da genel gecer olup olmadigi sorusuna yonlendirir Bu tur sorulara cevaben uygulanan yontemlerin isabetliligini gosteren birkac yontem gelistirilmistir ve ayrintili bilgi icin bkz Lyapunov stability ve structural stability Dinamik sistemin denkligi ya da kararliligi yorungelerin ile verilen ilk pozisyonu arasindaki esitligin kurulabileceginin gostergesidir Yorungelerin sistemle esitligini gostermek icin kullanilacak denklik kavramlari degistikce esitlik hesaplari da degisir Yorungenin ne tur oldugu daha onemli olabilir Bazi yorungeler diger yorungeler sistemin farkli durumlarini gosteren farkli egriler dogrularken periyodik olabilir Genelde hesaplamalar icin bu farkli egriler numaralandirilir farkli siniflara ayrilir ya da tek bir sinif altinda toplanir Tum bu yorungeleri siniflandirma calismalari bizi dinamik sistemler ustune niteliksel bir calismaya goturur koordinat degisiklikleriyle degismeyen ozelliklerin arastirilmasina ve siniflandirilmis yorungelerinden anlasilmis dinamik sistemlere birer ornektir Yorungelerin davranisinin yonelisleri egimleri vb bir parametreye gore fonksiyonu bir uygulama icin gerekli olan durumlar Bir parametre degistiginde dinamik sistemin davranisinin degistigini isaret eden dinamik sistemin yorungesi catallanabilir yorungeler ayrilabilir bkz ayrim noktalari Ornegin sadece periyodik bir yol izlerken bir anda rastgele bir yol izleyebilir sivinin turbulansinda oldugu gibi Yorungeler tamamen rastgele olabilir Bu durumda en uzun yorungeyi veya birden cok frakli davranan yorungeyi kullanarak ortalamanin alinmasi gerekebilir Ergodik sistemler icin ortalamalar oldukca iyi tanimlanmistir daha fazla bilgi icin bkz Ergodik teori ve daha detayli olan hiperbolik sistemler icinde ortalama hesaplamalari ortaya konmustur bkz Dinamik sistemlerin olasilikli halleri ustunde calismalarin kazandirdigi kavrayis istatistiksel mekanik ve kaos teorisinin temellerinin atilmasini saglamistir TarihcePek cok kisi dinamik sistemlerin kurucusu olarak Henri Poincare yi gorur Poincare New Methods of Celestial Mechanics gok mekaniginde yeni yontemler 1892 1899 ve Lectures on Celestial Mechanics gok mekanigi ustune dersler 1905 1910 isimli iki adet monografi yayinladi Bu kitaplarda uclu sistemler hareketleri ustundeki calismalarinin sonucunda elde ettigi yontemleri hatasiz bir sekilde uyguladi ve cozumleri ustunde daha detayli calismalar yapti frekanslari yorungelerin denklikleri asimptotlari vb Bu kagitlardaki calismalara gore Poincare in yineleme teorisini de iceriyorlardi Herhangi bir sistem yeterli bir zaman gectikten sonra yeterli ancak olculebilir zaman olcumun basladigi o ilk pozisyonuna cok yakin bir yere donuyordu Aleksandr Lyapunov pek cok onemli yaklasim yontemleri gelistirdi 1899 yilinda gelistirdigi bu yontemleri adi diferansiyel denklem kumelerinin kararliginin hesaplanmasini mumkun kiliyordu Dinamik sistemler icin modern kararlilik teorisini uretmistir 1913 yilinda George David Birkhoff un Poincare nin uclu sistemdeki ozel bir durum icin kanitlamasi ismini dunyaya tanitti 1927 yilinda simdi olarak bilinen ve ortaya atmis oldugu en uzun omurlu calismasi olan Dynamical Systems22 Nisan 2006 tarihinde Wayback Machine sitesinde i yayinladi Ergodik hipotezden edilmis fiziksel sezinin ve matematiksel hesaplamayla kombine olmasi en azindan prensipte istatistiksel mekanigin temel sorununun cozumunu olusturuyordu Ergodik teori ayni zamanda dinamikten esinlenmeler de icerir in de buyuk katkilari olmustur Ilk katkisi at nali haritasi ayrintili bilgi icin bkz ile dinamik sistemlerde kayda deger calismalar yapmistir Ayrica baskalarinin pek cok kez bas vurdugu bir arastirma programi da yapmistir 1964 yilinda kesintili bkz discrete dynamical system dinamik sistemlerin periyotlari ustunde calismasi sonucu gelistirmistir Teoremin cikarimlarindan birine gore sayi dogrusundaki kesintili bir dinamik sistem eger uc adet periyot noktasi barindiriyorsa diger her periyotlarda da periyodik nokta bulundurmak zorundadir Temel tanimlarDinamik bir sistem cok katli bir uzay lineer uzanan M diye adlandirilan gelisim evrilen fonksiyonlar Ft kumesini iceren uzay katmanindaki noktanin tekrar o katmana t gecen zamani ifade ederken t T donusunu gosteren bir harita olarak dusunulebilir Fonksiyonlardaki lineerlik kavrami kullanilan uygulamalara ve cok katlilarin tiplerine gore degisiklik gosterir T kumeleri icin birden fazla secim olanagi olabilir T gercek sayilar kumesi olarak alindiginda dinamik sistem akiskan olarak nitelenebilir bkz eger T sadece pozitif gercek sayilar kumesi olarak alindiginda dinamik sistem yari akiskan olarak nitelenir T tam sayi kumesi olarak alindiginda kaskat cascade selale ardisik kelimelerine karsilik gelir ya da bir plan sadece pozitif tam sayilar olarak alinirsa yari kaskat olarak nitelendirilebilir Ornekler Ft ile gosterilen gelisim fonksiyonu genelde hareket icin yazilmis diferansiyel denklemin bir cozumudur x v x displaystyle dot x v x Bu denklem faz uzayinda x0 herhangi bir ilk konum demektir dan baslayip x t yi izleyen yorungenin zamaninin turevini verir ustunde noktayla gosterilmis turev v x ile gosterilen vektor alani Min bu alanin her noktasinda faz uzayinin her noktasinda dinamik sistem icin hiz vektorunu olusturdugu lineer bir fonksiyondur Tabii ki bu hiz vektorleri M faz uzayinda uzay katmanindaki herhangi bir vektor degil herhangi bir x noktasi icin TxM ile gosterilen egim uzayinda bulunan vektorlerdir egim uzayindan kasit egimi olusturan ogelerin meydana getirdigi uzaydir Verilen Ft lineer fonksiyonundan otonom bir vektor alani turetilebilir v x icin ne yuksek dereceli turevlere ne de zaman parametresini kullanmaya gerek vardir cunku bu cokluklar sistemleri cok boyutlu uzayda acikladigimiz zaman ortadan kalkarlar Adi diferansiyel denklemlerin disinda kalan diger diferansiyel denklem turleri de gelisim kuralini ifade etmek icin kullanilabilir G x x 0 displaystyle G x dot x 0 denklemi kompleks karisikliklardan dolayi ifade edilmesi guclesen mekanik bir sistemin farkli bir gosterimine ornektir Ft gelisim fonksiyonunu anlatmak icin genelde adi diferansiyel denklemler kullanilir bu durumda M sonlu olan cok katli uzay boyutunu gosterir Dinamik sistemlerdeki pek cok kavram sonsuz katmanli uzaylara dek genisletilebilir Ornek ayrintili bilgi icin bkz banach sapaces tabii bu durumda kismi diferansiyel denklemler kullanilir Yirminci yuzyilin sonlarinda dinamik sistemlere kismi diferansiyel kullanarak yaklasmak oldukca yaygin bir kullanim olmustu Ileri duzey ornekler ayrintili bilgi icin orijinal isimlerine bakabilirsiniz Bifurkasyon is an example of a chaotic map and Lineer dinamik sistemlerLineer dinamik sistemler basit fonksiyonlar ya da siniflandirilmis yorungeler kullanilarak rahatlikla ifade edilebilen dinamik sistemler sinifidir N boyutlu Oklid uzayindaki uzay katmanlari nin herhangi biri N tane vektor ile gosterilebilir Lineer sistemler ustunde calismak mumkundur cunku cakisma prensibine uyarlar eger u t ve w t vektor alani icin olan diferansiyel denklemi saglarlarsa ilk konumu saglamalari sart degildir bunlarin toplami da saglar u t w t Akislar Bir akis icin sivinin akisi F x vektor alani uzay katmanindaki bir konum icin afin fonksiyonudur x ϕ x Ax b displaystyle dot x phi x Ax b bu denklemde A matris b sayilarin olusturdugu vektor x ise konum vektorune karsilik gelir Bu sistem cakisma prensibi lineerlik kullanilarak cozulebilir b 0 with A 0 olmasi durumunda bu denklem b yonundeki bir dogru denklemidir Ft x1 x1 bt displaystyle Phi t x 1 x 1 bt b sifir ve A 0 iken orijin akistaki bir denge noktasidir ve eger x0 0 ise yorunge sabit kalir Bundan farkli ilk konumlar icin bu hareket denklemi matrisin x0 ilk konumu icin uslu fonksiyonu kullanilarak olusturulabilir Ft x0 etAx0 displaystyle Phi t x 0 e tA x 0 b 0 iken Anin uzay katmaninin yapisini belirler Anin eigen degerleri ve kullanilarak ilk konumun denge noktasina dogru yaklasacagi ya da uzaklasacagini hesaplamak mumkundur A 0 oldugu durumlarda iki farkli ilk konum arasindaki mesafe ussel olarak degisir ya ussel olarak yaklasir ya da ussel olarak uzaklasirlar Lineer sistemler yaklasma durumlarinda ilk konumlara oldukca hassas bir sekilde baglidirlar ufak degisiklikler bile sonuclari degistirir Lineer olmayan sistemlerde bu gerekli ancak yine de yeterli gelmeyen kaotik teori icin de gerekli sartlardandir Haritalar dinamik sistemleri matris diferansiyel denklemi ile gosterilir ayrintili bilgi icin bkz xn 1 Axn b displaystyle x n 1 Ax n b A bir matrisi b ise bir vektoru gosteriyor Devamli olan durumlarda koordinatlarin dgisimi x x 1 A 1b denklemdeki b yi ortadan kaldirir Yeni koordinat sisteminde orijin haritada belli bir noktadadir ve lineer sistemin cozumleri A nx0 ile gosterilir haritanin cozumleri artik egrilerle degil uzay katmanlarindan atlayan noktalarla gosterilir Yorungeler haritanin ustundeki noktalar toplaminin olusturdugu egriler veya lifler seklinde duzenlenir Devamli olan durumlarda devamli fonksiyon gibi oldugu gibi Anin eigen degerleri ve vektorleri uzay katmaninin yapisini belirler Ornegin u1Anin eigen vektoru olsun birden kucuk eigen degeri icin a u1 noktalarindan gecen dogrular a R haritadaki sabit egrilerdir Bu dogrudaki noktalar sabit degerlerdir Kesintili dinamik sistemlere daha cok ornek icin bkz Yerel dinamiklerDinamik sistemlerin niteliksel ozellikleri koordinatlarda lineer degisimler olsa bile degismez bu aciklama bazen nitelik kavraminin tanimi olarak gorulur vektor alanindaki yalniz bir nokta v x 0 oldugu nokta lineer degisimler sonucu yine tek bir nokta olarak kalacaktir periyodik yorunge uzay katmanindaki bir dongu dugumdur ve bu uzay katmanindaki lineer donusumler sonucu yine ayni dongu olarak kalacaktir Dinamik sistemlerde uzay katmanindaki tek noktalar ve dongusel yorungelerin yakinlari yeterince iyi anlasilabilmektedir Dinamik sistemler ustundeki kapsamli calismalar gosteriyor ki koordinatlardaki degisimi degisimler spesifik olarak bilinmese de hesaplanabilir oldugu zaman kullanarak dinamik sistemlerin analizleri cok daha kolay oluyor Duzenleme ideallestirme Uzay katmaninin kucuk parcaciklarinin akisi cok basit formlara indirgenebilir Eger y v y 0 denkligini saglayan bir noktaysa o halde ynin cevresindeki vektor alaninin birbirine paralel ve ayni buyuklukte gecen vektorler olmasini saglayacak bir koordinat degisikligi yapilabilir bu degisiklik vardir Bu duzenleme teoremi olarak bilinir Duzenleme teoremi der ki tek noktalardan uzaktaki bir paketin icindeki noktanin dinamikleri bir dogruyu meydana getirir Bu paket bazen baska paketlerle birleserek buyuyebilir ve bu cozuldugunde tum uzay katmani M icin uzay integrallenebilirdir Cogu durumda bu paket tum uzay katmanini dolduramaz Vektor alaninda tek noktalar olabilir v x 0 oldugunda veya paketler bir noktaya yaklasirken git gide kuculebilir Bu genelin doldurulamayisi icin daha saglam bir neden yorungelerin paketten ciktiktan sonra belki diger paketlere ugradiktan sonra yine ayni yerine donmesi olabilir Eger yorunge bir donguye girerse bu vektor alanini duzenlemek tum paketler icin duzenlemek imkansiz olur periyodik yorungelerin komsuluklari Genel olarak periyodik bir yorungenin cevresi icin duzenleme teoremi kullanilamaz Poincare periyodik yorungenin yakinlarinin ustunde hesaplama yapilabilmesi icin bir donusum formulu gelistirdi g yorungesinde bir x0 noktasi secin ve uzay katmanindaki o noktaya yakin noktalarin v ye dik oldugunu gorun x0 iken Bu noktalara S g x0 Pontcare kesiti ayrintili bilgi icin bkz denir Simdi akis bir haritayi gosteriyor F S S Sden baslayip Se donen noktalar icin Her noktanin donmesi icin farkli farkli zamanlar gececektir ancak gecen zamanlar ilk konumdan baslayana yakin olacaktir x0 Periyodik yorunge ile Poincare kesitinin kesistigi nokta Poincare haritasinda belirli bir noktaya karsilik gelir F Dogrusal yer degistirme sonucu bu noktanin x 0 a denk gelecegi var sayilabilir Haritanin Taylor serileri ile gosterilisi F x J x O x2 yani koordinatlardaki bir degisikligin h sadece Fnin lineer kisminin basitlesmesine neden olacagi tahmin edilebilir h 1 F h x J x displaystyle h 1 circ F circ h x J cdot x Bu birlesim denklemi olarak bilinir Bu denklemin gecerli oldugu kosullarin bulunmasi dinamik sistemler ustundeki arastirmalarda en onemli onceliklerden biri olmustur Poincare ilk olarak tum fonksiyonlarin analiz edilebilir oldugunu varsayarak yaklasmis ve rezonans olmama kosulunu kesfetmistir Egerl1 ln sayilari J nin eigen degerleriyse ve eigen degerlerinden biri lineer olarak iki veya daha fazlasinin kombine edilmis haliyse bu sayilar birbirinin rezonansi olmalidir li terimleri diger eigen degerlerinin katlari h fonksiyonunda payda da yer alirsa rezonans olmama kosulu ayni zamanda kucuk bolen problemi olarak da bilinir Birlesim girisim Sonuclari Birlesim denkleminin sonuclari olabilmesi Jnin eigen degerlerine ve hnin derecesinin bir olmasina baglidir lineer olmasi icin Jnin herhangi ozel bir simetriye sahip olmasina gerek olmadigindan Jnin eigen degerleri karmasik sayilar olabilir jnin eigen degerleri birim cember uzerinde olmadiginda F ustundeki sabit x0 noktalari sabit hiperbolik noktalar olarak adlandirilir ve eigen degerleri cember uzerinde olmasinin yani sira karmasik sayilar olurlarsa eliptik olarak adlandirilir Hiperbolik oldugu durumda lineer haritadaki sabit J x noktasinin komsulugunun devamli oldugu fonksiyonu verecek olan sartlari ortaya koyar Hiperbolik durum ayni zamanda yapisal kararliliga da sahiptir Vektor alanindaki kucuk degisiklikler Poincare haritasinda sadece kucuk degisiklikler yaratacak ve bu kucuk degisiklikler Jnin eigen degerlerinde ufak degisiklikleri meydana getirecek karmasik sayilar duzleminde ki bu yeni eigen degerlerinin gorunumu yine hiperbolik bir sekle sahip olacak teoremi eliptik noktanin komsulugunun davranisini aciklar Bifurkasyon catallanma teorisiGelisim haritasi ya da ondan turetilen vektor alani Ft m gibi bir parametreye bagli oldugu zaman uzay katmaninin yapisi da bu parametreye bagli olur Belli bir m0 degerine ulasmadan bu parametredeki degisimler uzay katmaninda bir degisiklik yaratmazlar O nokta asildiktan sonra uzay katmani olculebilir bir sekilde degisir degisim gozlemlenecek bir sekilde ve dinamik sistemde bir catallanma meydana gelir Bifurkasyon teorisi uzay katmaninin yapisi ozellikle sabit noktalar bakz periyodik yorungeler ya da sabit yumrular bkztorus icin ve m parametresi icin davranisini degisimini inceler Catallanma noktasinda yapi kararliligini degistirebilir yeni yapilar olusturmak uzere bolunebilir ya da diger yapilarla birlesebilir Taylor serileriyle yaklasimlari kullanarak ve koordinat degisikligi nedeniyle eksik kalan yok olan parametreleri anlayarak dinamik sistemlerdeki catallanmalari siniflandirmak mumkun olabilir Fm ailesine ait bir hiperboligin x0 noktasindaki catallanmalari DFm x0 ile sistemin catallanma noktasindaki ilk turevi alinarak hesaplanabilir Haritada DFmnin eigen degerlerinin bir cember ustunde olmasi orada catallanma olacagini gosterir Bir akista eigen degerleri sanal eksen ustunde oldugunda catallanma olur Daha fazla bilgi icin bkz Bazi catallanmalar uzay katmaninda oldukca karisik yapilarin meydana cikmasina sebep olurlar Oregin periyodik bir catallanmanin bit yumruya yumrunun da oldukca karmasik bir cekiciye donmesini anlatir ayrintili bilgi icin bkz Baska bir ornekle sabit bir periyodik yorungenin cifter periyodik catallanmalara ayrildiini anlatir ayrintili bilgi cin bkz Ergodik sistemlerPek cok dinamik sistemde hacmin v boyutlu bir hacim uzay katmanindan bagimsiz olacagi bir koordinat ekseni secmek mumkundur Bu Newton un kanunlarina dayandirilarak uretilmis sistemlerde mumkundur kooridantlar konum ve momentum olacak sekilde bir koordinatlar ekseni ve hacmin birimi konum momentum birimleri cinsinden belirtildikce Akista A kumesinden bir alt kume F t A fonksiyonuyla isleme sokulur ve uzay katmanindan bagimsizli su denklikle gosterilir vol A vol Ft A displaystyle mathrm vol A mathrm vol Phi t A Hamilton mekaniginde koordinatlar bilindikce genel calismalar icin elverisli bir momentum degeri hacimden akis sirasinda hacmin korunan sistemler icin bulunabilir Hacmin ile bulunabilir ayrintili bilgi icin bkz Bir Hamilton sisteminde her cesit kozum momentum degerini bulmak ilk sartlar bilindigi takdirde mumkun degildir Cunku enerji korunumu sadece ilk sartlardaki enerji miktari ile esit olan durumlar icin uygulanabilirdir W adli enerji kabugundaki enerji miktariyla ayni olan enerjiler o uzay katmaninin alt kumeleridirler Enerji katmaninin hacmi Liouville hesabiyla bulunur ve gelisim sartlari altinda korunurdur Akislarda hacimleri korunan sistemlerde Poincare Poincare yineleme teorisini ortaya koydu Bu teoreme gore bir uzay katmaninin sonlu bir Liouville hacmine sahip oldugunu ve Fnin hacim korunumlu bir uzay katmani haritasi ve Anin da uzay katmaninin alt kumesi oldugunu var sayin O halde neredeyse her bir A noktasi tekrar A noktasina sonsuz siklikta doner Poincare nin yineleme teorisi tarafindan nin carpisan atomlarin olusturdugu dinamik sisteminden entropinin arttigi yonundeki cikarimina itiraz etmek icin kullanildi Boltzmann in calismasina yoneltilen sorulardan biri ortalama zaman ve ortalama uzayin arasindaki esitlik olma ihtimaliyle ilgiliydi ergodik hipotez olarak adlandirdigi Hipoteze gore zamanin uzunlugu vektorel nun A bolgesinde katettigi miktar vol A vol W idi Ergodik hipotezin istatistiksel mekanigin gelisimi icin temel tas olmadigi ve ergodik benzeri diger serilerin iliskili fiziksel sistemlerin genel gorunusunu cikarim yapilabilecek gorunus kisitladigi ortaya atildi ergodik sistemlere fonksiyonel analiz kullanarak yaklasti a uzay katmanindaki her bir sayiyla ornegin ani basinc veya ortalama yukseklik iliskilendirilmis olan bir fonksiyon olsun Gozlemlenebilir degerleri baska bir zaman gelisim fonksiyonu f t kullanarak olculebilir Bu da bizi transfer operatorune getirir U t Uta x a F t x displaystyle U t a x a Phi t x Lineer operator U un dagiliminin ozellikleri uzerinde calisarak F t in ergodik ozelliklerini siniflamak mumkundur Koopman yaklasimini kullanarak akisin gozlemlenebilir bir fonksiyonu oldugu durumlar icin sonlu boyutlu lineer olmayan bir katman icin gecerli bir problemde F t fonksiyonu Uyu iceren sonlu boyutlu bir harita ile ifade edilebilir Liouville hesabi sadece enerji kabugu W nun ortalama hesaplamlari kullanildiginda gecerlidir ayrintili bilgi icin bkz Bir yonerge boyunca olan zamanin ortalamasinin uzayin ortalamasinin vektorel esdeger olusu Boltzmann faktoruyle olculur bkz Bu fikir Sinai Bowen ve Ruelle SRB hesabi gibi bilim insanlari tarafindan daha buyuk sistem siniflari icin korunmayan sistemlerde dahil genellenmistir kaotik sistemler icin Boltzmann hesabi yerine kullanilmistir Lineer olamayan dinamik sistemler ve kaos Basit lineer olmayan denklemler ve hatta parcali lineer sistemler bazen ongorulmemis davranislar sergileyebilir rastgele davranir gibi temelde tanimli fonksiyonlar olsalar bile Bu rast gele gibi gorunen davranis kaos olarak adlandirilir Anosov kaotik sistemler olarak adlandirilan bu sistemlere benzer davranislar sergileyen dinamik sistemler tanimlamistir yuksek kesinliklerle ayrintili bilgi icin bkz Hiperbolik sistemlerde egim uzaylarinin esas yorungeye dik oldugu sistemler iki kisma ayrilabilir yorungeye yakinsak noktalar icerenler kararli cokkatlilar ve yorungeye iraksak noktalar iceren karasiz cokkatlilar ler Matematigin bu dali dinamik sistemlerin uzun donem davranislarini arastirir Yani sadece spesifik bir kismina odaklanmak o dinamik sistem icin genel cozumler uretmemize yardimci olmaz bu yuzden bu dal boyle sorulari sormak yerine ancak sistem uzun bir donem sonra kararlilik kazanacaksa bu dinginlik konumlari hangi zamana denk gelir ya da uzun donem davranisi sergileyen bu sistem kendisinin ilk sartlarindan bagimsiz mi hareket eder gibi sorularla ugrasir Karmasik sistemlerin kaotik davranisindan bahsetmedigimize dikkat edin Meteoroloji karmasik sistemler hatta kaotik davranislar sergileyen sistemler ustune uzun zamanlar boyunca calisma yapmistir Koss teorisi hep sasirtici olmustur cunku dikkat edilmeyen onemsiz sistemlerin dahi kaos icerdigi gorulmustur tek ikinci derece polinom dinamik sistemdir atnali haritasi parcali lineer sistem bir ornektir ayrintili bilgi icin bkz Geometrik tanim Dinamik sistem bir degiskenler grubudur M f T displaystyle langle mathcal M f mathcal T rangle M displaystyle mathcal M bircok katliyi gosterir Banach veya Oklid uzayindaki T displaystyle mathcal T ise zamanin tanim kumesidir pozitif gercek sayilar tam sayilar vb ile gosterilebilir ve f ise t f t ile veya f t gosterilen gelisim kurali t T displaystyle t in mathcal T iken ve cokkatlinin diferansiyelidir ayrintili bilgi icin bkz Yani f zamana bagli T displaystyle mathcal T nin kendi katlarina bagli degisiminin haritasidir Baska bir deyisle f t bir diferansiyellenebilir morfizmadir T displaystyle mathcal T nin tanimli oldugu her zaman tdegeri cin Teorik tanimin hesaplanmasi Dinamik sistem formullerle tanimlanabilir denkligin korundugu donusumler buna bir ornek olabilir X S m t dortlusu kullanilarak Diyelim ki X bir matematiksel kume ve S ise X ile olan ayrintili bilgi icin bkz sonuc olarak X S ikilisi olculebilir bir uzay katanidir m de sigma cebiri ile iliskilendirilmis sonlu bir hesaplanma olsun ve X S m uclusu olasiliksal uzayi olusturur ayrintili bilgi icin bkz Bir haritain t X X adli olculebilir bir fonksiyonu sadece s S nun t 1s S displaystyle tau 1 sigma in Sigma oldugu kosullarda vardirve bir haritanin korunur denkligi hesabi her s S icin sadece m t 1s m s displaystyle mu tau 1 sigma mu sigma oldugunda vardir Yukaridakileri kombine edersek korunur denkligi hesabi olan bir harita icin Xin yine X e dondugu S ile hesaplanabilir ve bu hesap korunurdur X S m t dortlusu t icin ifade edilirse dinamik sistem olarak gosterilebilir t haritasi somut bir zamana bagli gelisimsel dinamik sistemdir Bundan dolayi kesintili dinamik sistemler icin bu fonksiyon tekrarlanir tn t t t displaystyle tau n tau circ tau circ cdots circ tau nlersn tam sayi oldugu degerler icin Devamli dinamik sistemler icin bu t haritasi sonlu zamanla geisen bir gelisim fonksiyonu olarak dusunulebilir ve daha karmasik sistemler kurulabilir Dinamik sistem ornekleriis an example of a chaotic piecewise linear map andCok boyutlu genellemeDinamik sistemler tek bir bagimsiz degisken ustune kuruludur genelde bu degisken zamandir Daha genel sistem siniflari coklu bagimsiz degiskenler ustune kuruludur ve bu yuzden cok boyutlu sistemler olarak adlandirilirlar Bu tip sistemler matematiksel modelleme icin kullanislidir ornegin goruntu isleme Ayrica bakinizKaynakca Strogatz S H 2001 Nonlinear dynamics and chaos with applications to physics biology and chemistry Perseus publishing Katok A amp Hasselblatt B 1995 Introduction to the modern theory of dynamical systems Cambridge Cambridge Holmes Philip Poincare celestial mechanics dynamical systems theory and chaos Physics Reports 193 3 1990 137 163 Ileri duzey okulamar icinWorks providing a broad coverage and 1978 Foundations of mechanics Benjamin Cummings ISBN 0 8053 0102 X available as a reprint ISBN 0 201 40840 6 Encyclopaedia of Mathematical Sciences ISSN 0938 0396 has a sub series on dynamical systems with reviews of current research Christian Bonatti Lorenzo J Diaz Marcelo Viana 2005 Dynamics Beyond Uniform Hyperbolicity A Global Geometric and Probabilistic Perspective Springer ISBN 3 540 22066 6 KB1 bakim Birden fazla ad yazar listesi link 1967 Differentiable dynamical systems Bulletin of the American Mathematical Society 73 6 ss 747 817 doi 10 1090 S0002 9904 1967 11798 1 Ozgun usluplari olan giris kitaplari V I Arnold 1982 Mathematical methods of classical mechanics Springer Verlag ISBN 0 387 96890 3 and Wellington de Melo 1982 Geometric theory of dynamical systems an introduction Springer Verlag ISBN 0 387 90668 1 David Ruelle 1989 Elements of Differentiable Dynamics and Bifurcation Theory Academic Press ISBN 0 12 601710 7 Tim Bedford Michael Keane and Caroline Series eds 1991 Ergodic theory symbolic dynamics and hyperbolic spaces Oxford University Press ISBN 0 19 853390 X KB1 bakim Birden fazla ad yazar listesi link and 1992 Dynamics the geometry of behavior 2nd edition Addison Wesley ISBN 0 201 56716 4 Ders kitaplari Kathleen T Alligood Tim D Sauer and 2000 Chaos An introduction to dynamical systems Springer Verlag ISBN 0 387 94677 2 Oded Galor 2011 Discrete Dynamical Systems Springer ISBN 978 3 642 07185 0 Anatole Katok and Boris Hasselblatt 1996 Introduction to the modern theory of dynamical systems Cambridge ISBN 0 521 57557 5 Guenter Ludyk 1985 Stability of Time variant Discrete Time Systems Springer ISBN 3 528 08911 3 Stephen Lynch 2010 Dynamical Systems with Applications using Maple 2nd Ed Springer ISBN 0 8176 4389 3 Stephen Lynch 2007 Dynamical Systems with Applications using Mathematica Springer ISBN 0 8176 4482 2 Stephen Lynch 2004 Dynamical Systems with Applications using MATLAB Springer ISBN 0 8176 4321 4 James Meiss 2007 Differential Dynamical Systems SIAM ISBN 0 89871 635 7 Morris W Hirsch and Robert Devaney 2003 Differential Equations dynamical systems and an introduction to chaos Academic Press ISBN 0 12 349703 5 Julien Clinton Sprott 2003 Chaos and time series analysis Oxford University Press ISBN 0 19 850839 5 1994 Nonlinear dynamics and chaos with applications to physics biology chemistry and engineering Addison Wesley ISBN 0 201 54344 3 2012 Providence American Mathematical Society ISBN 978 0 8218 8328 0 26 Haziran 2012 tarihinde kaynagindan arsivlendi Erisim tarihi 21 Ocak 2015 Stephen Wiggins 2003 Introduction to Applied Dynamical Systems and Chaos Springer ISBN 0 387 00177 8 Populer kaynaklar and 1996 Celestial Encounters Princeton ISBN 0 691 02743 9 1988 Chaos Making a New Science Penguin ISBN 0 14 009250 1 1990 Mathematics and the Unexpected Paperback University Of Chicago Press ISBN 0 226 19990 8 Ian Stewart 1997 Does God Play Dice The New Mathematics of Chaos Penguin ISBN 0 14 025602 4 Dis baglantilarInteractive applet for the Standard and Henon Maps13 Haziran 2011 tarihinde Wayback Machine sitesinde by A Luhn in Monash University s Virtual Lab Arxiv preprint server12 Agustos 2013 tarihinde Wayback Machine sitesinde has daily submissions of non refereed manuscripts in Dinamik sistemler DSWeb13 Agustos 2006 tarihinde Wayback Machine sitesinde provides up to date information on dynamical systems and its applications Encyclopedia of dynamical systems16 Mayis 2007 tarihinde Wayback Machine sitesinde A part of Scholarpedia peer reviewed and written by invited experts Nonlinear Dynamics16 Ekim 2007 tarihinde Wayback Machine sitesinde Models of bifurcation and chaos by Elmer G Wiens Oliver Knill11 Mart 2016 tarihinde Wayback Machine sitesinde has a series of examples of dynamical systems with explanations and interactive controls Sci Nonlinear FAQ 2 0 Sept 2003 5 Nisan 2007 tarihinde Wayback Machine sitesinde provides definitions explanations and resources related to nonlinear science Cevrimici kitaplar ve ders notlari Geometrical theory of dynamical systems Nils Berglund s lecture notes for a course at at the advanced undergraduate level Dynamical systems22 Nisan 2006 tarihinde Wayback Machine sitesinde George D Birkhoff s 1927 book already takes a modern approach to dynamical systems Chaos classical and quantum25 Temmuz 2011 tarihinde Wayback Machine sitesinde An introduction to dynamical systems from the periodic orbit point of view An introduction to the development of mathematical models of dynamic systems Learning Dynamical Systems12 Temmuz 2006 tarihinde Wayback Machine sitesinde Tutorial on learning dynamical systems Ordinary Differential Equations and Dynamical Systems26 Haziran 2012 tarihinde Wayback Machine sitesinde Lecture notes by arastirma gruplari Dynamical Systems Group Groningen3 Nisan 2007 tarihinde Wayback Machine sitesinde IWI University of Groningen Chaos UMD12 Haziran 2005 tarihinde Wayback Machine sitesinde Concentrates on the applications of dynamical systems SUNY Stony Brook Lists of conferences researchers and some acik sorular Center for Dynamics and Geometry14 Temmuz 2014 tarihinde Wayback Machine sitesinde Penn State Control and Dynamical Systems 30 Mayis 2014 tarihinde Wayback Machine sitesinde Caltech Ecole Polytechnique Federale de Lausanne EPFL University of Bremen University of Oxford Non Linear Dynamics Group 3 Mart 2016 tarihinde Wayback Machine sitesinde Instituto Superior Tecnico Technical University of Lisbon Dynamical Systems 2 Haziran 2017 tarihinde Wayback Machine sitesinde IMPA Instituto Nacional de Matematica Pura e Applicada Nonlinear Dynamics Workgroup 21 Ocak 2015 tarihinde Wayback Machine sitesinde Institute of Computer Science Czech Academy of Sciences Simulation software based on Dynamical Systems approach FyDiK20 Ocak 2009 tarihinde Wayback Machine sitesinde iDMC olu kirik baglanti simulation and dynamical analysis of nonlinear models
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State