Primoriyel (İngilizce İngilizce: prime (=asal)'dan), matematikte ve bilhassa sayı teorisinde doğal sayılardan doğal sayılara tanımlanmış faktöriyele benzer şekilde art arda pozitif tam sayıları çarpacağı yerde sadece asal sayıları çarpar.


Birbiriyle çelişen iki tanımda kullanılan değişkenin mânâsı farklı yorumlanmaktadır: birincisi değişkeni asal sayıların sıralaması olarak yorumlar, dolayısıyla . İkinci yorumu değişkeni birbiriyle çarpılacak asal sayılara işaret eder ve dolayısıyla her bileşik sayı için bir önceki değerle aynı değeri alır. Bu maddenin devamında ikinci tanım kullanılacaktır.
Primoriyel adı, bu fonksiyonla faktöriyel arasındaki analojiye işaret eden tarafından verilmiştir; faktöryel nasıl faktörlere ilgiliyse primoriyel de asal sayılarla (İng. İngilizce: prime numbers veya kısaca İngilizce: primes) benzer şekilde ilgilidir.
Asal sayılar için tanımı
n'inci asal sayı pn için primoriyel pn#, ilk n asalın çarpımı olarak tarif edilir:
Burada pk k'inci asal sayıdır.
Mesela p5#, ilk beş asalın çarpımını gösterir:
İlk altı primoriyel pn# are:
Diziye p0# = 1 de olarak eklenmiştir.
Asimtotik olarak primoriyel pn#,
fonksiyonuna göre artarlar. Burada 
Doğal sayılar için tanımı
Genelde n pozitif tam sayısı için n# ≤ n olan bütün asalların çarpımı olarak da tarif edilebilir: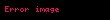
Burada 
Bu tanım, aynı zamanda şuna da eşittir.
Mesela 12#, 12'den küçük asal sayıların çarpımıdır:

şeklinde hesaplanır.
Bu tanıma göre ilk 12 primoriyel n# şöyledir:
- 1, 2, 6, 6, 30, 30, 210, 210, 210, 210, 2310, 2310.
Görüldüğü gibi bileşik n için her terim n#, tarifinde de görüldüğü gibi bir önceki terimin eşidir (n − 1)#. Yukarıdaki örnekte 12 bileşik sayı olduğundan 12# = p5# = 11#'dir.
n#'nin tabii logaritması birinci olup 

n# primoriyeli
fonksiyonuna göre büyür.
Bütün bilinen asal sayıları çarpma fikri asal sayıların sonsuzluğu ile ilgili bâzı ispatlarda geçmekte olup başka bir asal sayının varlığını türetmek için kullanılır.
Özellikler ve uygulamalar
Primoriyeller, aramada bir rol oynar. Mesela 2236133941 + 23# bir asal sayıdır ve on üç asal sayıdan oluşan bir dizinin başıdır. Bu dizi, yukarıdaki asal sayıya 23# eklemekle elde edilir, on üçüncü ve sonuncu elemanı da 5136341251'dir. 23#, aynı zamanda on beş ve on altı asalın aritmetik progresyonunda ortak farkı teşkil eder.
Her primoriyellerin çarpımıdır (mesela = 2·6·30).
Primoriyeller olup kendilerinden küçük herhangi bir sayıdan daha fazla farklı vardır. Her primoriyel n için 

Görünüm
Birden büyük pozitif tam sayılar için Riemann zeta fonksiyonu, primorieller ve 
Primoriyellerin tablosu
| n | n# | pn | pn# |
|---|---|---|---|
| 0 | 1 | asal yok | |
| 1 | 1 | 2 | 2 |
| 2 | 2 | 3 | 6 |
| 3 | 6 | 5 | 30 |
| 4 | 6 | 7 | 210 |
| 5 | 30 | 11 | 2310 |
| 6 | 30 | 13 | 30030 |
| 7 | 210 | 17 | 510510 |
| 8 | 210 | 19 | 9699690 |
| 9 | 210 | 23 | 223092870 |
| 10 | 210 | 29 | 6469693230 |
| 11 | 2310 | 31 | 200560490130 |
| 12 | 2310 | 37 | 7420738134810 |
| 13 | 30030 | 41 | 304250263527210 |
| 14 | 30030 | 43 | 13082761331670030 |
| 15 | 30030 | 47 | 614889782588491410 |
| 16 | 30030 | 53 | 32589158477190044730 |
| 17 | 510510 | 59 | 1922760350154212639070 |
| 18 | 510510 | 61 | 117288381359406970983270 |
| 19 | 9699690 | 67 | 7858321551080267055879090 |
| 20 | 9699690 | 71 | 557940830126698960967415390 |
Kaynakça
- ^ a b Eric W. Weisstein, Primorial (MathWorld), Eric W. Weisstein. "Primorial". 30 Nisan 2016 tarihinde kaynağından . Erişim tarihi: 6 Mayıs 2015.
- ^ a b (OEIS'de A002110 dizisi)
- ^ (OEIS'de A034386 dizisi)
- ^ Eric W. Weisstein, Chebyshev Functions (MathWorld)
- ^ "Sloane's A002182 : Highly composite numbers", The . OEIS Foundation.
- ^ Mező, István (2013). "The Primorial and the Riemann zeta function". The American Mathematical Monthly. 120 (4). s. 321.
- Harvey Dubner, "Factorial and primorial primes". , 19, 197–203, 1987.
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Primoriyel Ingilizce Ingilizce prime asal dan matematikte ve bilhassa sayi teorisinde dogal sayilardan dogal sayilara tanimlanmis faktoriyele benzer sekilde art arda pozitif tam sayilari carpacagi yerde sadece asal sayilari carpar pn in n in fonksiyonu olarak logaritmik egrisi n in n nin fonksiyonu diagraminin kirmizi noktalar n le kiyasi Her iki egri logaritmiktir Birbiriyle celisen iki tanimda kullanilan degiskenin manasi farkli yorumlanmaktadir birincisi degiskeni asal sayilarin siralamasi olarak yorumlar dolayisiyla Ikinci yorumu degiskeni birbiriyle carpilacak asal sayilara isaret eder ve dolayisiyla her bilesik sayi icin bir onceki degerle ayni degeri alir Bu maddenin devaminda ikinci tanim kullanilacaktir Primoriyel adi bu fonksiyonla faktoriyel arasindaki analojiye isaret eden tarafindan verilmistir faktoryel nasil faktorlere ilgiliyse primoriyel de asal sayilarla Ing Ingilizce prime numbers veya kisaca Ingilizce primes benzer sekilde ilgilidir Asal sayilar icin tanimin inci asal sayi pn icin primoriyel pn ilk n asalin carpimi olarak tarif edilir pn k 1npk displaystyle p n prod k 1 n p k Burada pk k inci asal sayidir Mesela p5 ilk bes asalin carpimini gosterir p5 2 3 5 7 11 2310 displaystyle p 5 2 times 3 times 5 times 7 times 11 2310 Ilk alti primoriyel pn are 1 2 6 30 2310 OEIS de A002110 dizisi Diziye p0 1 de olarak eklenmistir Asimtotik olarak primoriyel pn pn e 1 o 1 nlog n displaystyle p n e 1 o 1 n log n fonksiyonuna gore artarlar Burada o displaystyle o cdot kucuk o gosterimidir Dogal sayilar icin tanimiGenelde n pozitif tam sayisi icin n n olan butun asallarin carpimi olarak da tarif edilebilir n i 1p n pi pp n displaystyle n prod i 1 pi n p i p pi n Burada p n displaystyle scriptstyle pi n OEIS de A000720 dizisi olup n olan asal sayilarin kac tane oldugunu haber verir Bu tanim ayni zamanda suna da esittir n 1if n 1n n 1 if n gt 1 amp n is prime n 1 if n gt 1 amp n is composite displaystyle n begin cases 1 amp text if n 1 n times n 1 amp text if n gt 1 And n text is prime n 1 amp text if n gt 1 And n text is composite end cases Mesela 12 12 den kucuk asal sayilarin carpimidir 12 2 3 5 7 11 2310 displaystyle 12 2 times 3 times 5 times 7 times 11 2310 p 12 5 displaystyle scriptstyle pi 12 5 oldugundan bu deger 12 pp 12 p5 2310 displaystyle 12 p pi 12 p 5 2310 seklinde hesaplanir Bu tanima gore ilk 12 primoriyel n soyledir 1 2 6 6 30 30 210 210 210 210 2310 2310 Goruldugu gibi bilesik n icin her terim n tarifinde de goruldugu gibi bir onceki terimin esidir n 1 Yukaridaki ornekte 12 bilesik sayi oldugundan 12 p5 11 dir n nin tabii logaritmasi birinci olup 8 n displaystyle theta n veya ϑ n displaystyle vartheta n seklinde yazilir Bu fonksiyon buyuk n ler icin lineer n ye yaklasir n primoriyeli ln n n displaystyle ln n sim n fonksiyonuna gore buyur Butun bilinen asal sayilari carpma fikri asal sayilarin sonsuzlugu ile ilgili bazi ispatlarda gecmekte olup baska bir asal sayinin varligini turetmek icin kullanilir Ozellikler ve uygulamalarPrimoriyeller aramada bir rol oynar Mesela 2236133941 23 bir asal sayidir ve on uc asal sayidan olusan bir dizinin basidir Bu dizi yukaridaki asal sayiya 23 eklemekle elde edilir on ucuncu ve sonuncu elemani da 5136341251 dir 23 ayni zamanda on bes ve on alti asalin aritmetik progresyonunda ortak farki teskil eder Her primoriyellerin carpimidir mesela 2 6 30 Primoriyeller olup kendilerinden kucuk herhangi bir sayidan daha fazla farkli vardir Her primoriyel n icin ϕ n n displaystyle phi n n kesri kendisinden kucuk her tam sayi icin olan kesirden kucuktur Burada ϕ displaystyle phi GorunumBirden buyuk pozitif tam sayilar icin Riemann zeta fonksiyonu primorieller ve Jk n displaystyle J k n kullanarak hesaplanabilir z k 2k2k 1 r 2 pr 1 kJk pr k 2 3 displaystyle zeta k frac 2 k 2 k 1 sum r 2 infty frac p r 1 k J k p r quad k 2 3 dots Primoriyellerin tablosun n pn pn 0 1 asal yok1 1 2 22 2 3 63 6 5 304 6 7 2105 30 11 23106 30 13 300307 210 17 5105108 210 19 96996909 210 23 22309287010 210 29 646969323011 2310 31 20056049013012 2310 37 742073813481013 30030 41 30425026352721014 30030 43 1308276133167003015 30030 47 61488978258849141016 30030 53 3258915847719004473017 510510 59 192276035015421263907018 510510 61 11728838135940697098327019 9699690 67 785832155108026705587909020 9699690 71 557940830126698960967415390Kaynakca a b Eric W Weisstein Primorial MathWorld Eric W Weisstein Primorial 30 Nisan 2016 tarihinde kaynagindan Erisim tarihi 6 Mayis 2015 a b OEIS de A002110 dizisi OEIS de A034386 dizisi Eric W Weisstein Chebyshev Functions MathWorld Sloane s A002182 Highly composite numbers The OEIS Foundation Mezo Istvan 2013 The Primorial and the Riemann zeta function The American Mathematical Monthly 120 4 s 321 Harvey Dubner Factorial and primorial primes 19 197 203 1987 Ayrica bakiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State