Bu maddedeki bilgilerin için ek kaynaklar gerekli. (Kasım 2023) () |
RSA, güvenliği tam sayıları çarpanlarına ayırmanın algoritmik zorluğuna dayanan bir tür açık anahtarlı şifreleme yöntemidir. 1978’de Ron Rivest, Adi Shamir ve Leonard Adleman tarafından bulunmuştur. Bir RSA kullanıcısı iki büyük asal sayının çarpımını üretir ve seçtiği diğer bir değerle birlikte ortak anahtar olarak ilan eder. Seçilen asal çarpanları ise saklar. Ortak anahtarı kullanan biri herhangi bir mesajı şifreleyebilir, ancak şu anki yöntemlerle eğer ortak anahtar yeterince büyükse sadece asal çarpanları bilen kişi bu mesajı çözebilir. RSA şifrelemeyi kırmanın çarpanlara ayırma problemini kırmak kadar zor olup olmadığı hala kesinleşmemiş bir problemdir.
Tarihi
Birleşik Krallık haber alma teşkilatı GCHQ’da çalışan İngiliz matematikçi 1973’te kurum içi bir dokümanda eşdeğer bir sistemi açıkladı. Fakat bu sistemi hayata geçirmek için epeyce pahalı bilgisayarların kullanılması gerekiyordu ve bilindiği kadarıyla hiç kullanılmadı. Fakat Cocks’un buluşu 1998’e kadar çok gizli olduğu gerekçesiyle açığa çıkarılmadı. Rivest, Shamir ve Adleman RSA yöntemini Cocks’un çalışmasından bağımsız olarak tasarladılar.
RSA algoritması 1978’de MIT’de Ron Rivest, Adi Shamir ve Leonard Adleman tarafından açıklandı. RSA harfleri soyisimlerinin baş harflerini temsil etmektedir.
Patent
MIT'e 20 Eylül 1983'te algoritmayı kullanan bir "Şifreleme iletişim sistemi ve yöntemi" için ABD Patenti 4,405,829 verildi.Patent 21 Eylül 2000'de sona erecek olsa da (patent süresi 17 yıldır), algoritma iki hafta önce 6 Eylül 2000'de RSA Security tarafından kamuya açıklandı. Algoritmanın ayrıntılı bir açıklaması Scientific American'ın Ağustos 1977 sayısında Matematik Oyunları sütununda yayınlandığından, patent başvurusunun Aralık 1977 dosyalama tarihinden önce dünyanın geri kalanının çoğunda düzenlemeler başka yerlerde ve sadece ABD patenti verildi. Cocks'un çalışmaları herkes tarafından biliniyor olsaydı, ABD'deki bir patent de yasal olmayacaktı.
'nin patent özetinden,
Sistem bir kodlama cihazına sahip en az bir terminale ve bir kod çözme cihazına sahip en az bir terminale bağlanmış bir iletişim kanalı içerir. Aktarılacak bir mesaj, önceden belirlenmiş bir kümede M sayısı olarak kodlanarak kodlama terminalindeki şifreli metne şifrelenir. Bu sayı daha sonra önceden belirlenmiş bir güce (istenen alıcı ile ilişkili) yükseltilir ve son olarak hesaplanır. Kalan veya kalıntı C, ... üssel sayı, önceden belirlenmiş iki asal sayının çarpımına (hedeflenen alıcı ile ilişkili) bölündüğünde hesaplanır.
İşlemler
RSA algoritması anahtar üretimi, şifreleme ve şifre çözme olmak üzere 3 basamaktan oluşmaktadır.
Anahtar Üretimi
RSA için bir ortak anahtar bir de özel anahtar gerekir. Ortak anahtar herkes tarafından bilinir ve mesajı şifrelemek için kullanılır. Bir ortak anahtarla şifrelenmiş mesaj sadece özel anahtarla çözülebilir. RSA anahtarları şu şekilde oluşturulur:
- İki adet birbirinden değişik asal sayı seçin, bunların adını da
ve
koyalım.
- Güvenlik amacıyla p ve q sayıları rastgele seçilmeli ve yakın uzunlukta olmalıdırlar. Bu sayılar asallık testi kullanılarak etkin bir şekilde bulunabilir.
hesaplayın.
özel ve ortak anahtarlar için mod değeri olarak kullanılacaktır.
- Bu sayıların totientı olan
hesaplayın.
- Bir tam sayı üretin ve adını da
koyun. Bu sayı,
koşuluna uygun olmalı ve
ile en büyük ortak böleni 1 olmalıdır (başka bir deyişle
ve
kendi aralarında asal olmalıdır).
ortak anahtar olarak açıklanır.
- Bit uzunluğu kısa olan ve küçük sahip
değerleri (yaygın olarak 0x10001 = 65,537) daha verimli şifreleme sağlarlar. Fakat küçük
değerleri (örneğin 3) bazı durumlarda güvenliği azaltabilir.
olacak şekilde bir
'yi belirleyin.
özel anahtar üssü olarak saklanır.
değeri genellikle kullanılarak hesaplanır.
Ortak anahtar mod değeri olan 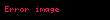
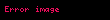
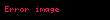
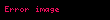



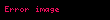
Şifreleme
Alice ortak anahtarı (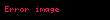
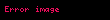


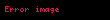

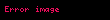
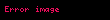
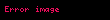
Şifre Çözme
Alice 
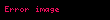
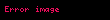
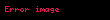
Alice 

Örnek
- İki farklı asal sayı seçelim.
ve
olsun.
değerini hesaplayalım. 61 × 53 = 3233.
- Totient değerini hesaplayalım.
.
- 1 ile 3120 arasında 3120 ile aralarında asal olan bir
değeri seçelim.
değerini asal seçersek sadece 3120’nin böleni olup olmadığını kontrol etmemiz gerekir.
olsun.
’yi
’nin mod
’deki çarpmaya gore tersi olarak hesaplayalım.
.
Ortak Anahtar: 


Özel Anahtar: 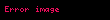

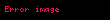
Örneğin 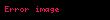
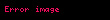

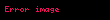
Tüm bu hesaplamalar karesini alarak üs alma yöntemiyle hızlı bir şekilde gerçekleştirilebilir.
Düz RSA karşısındaki Saldırılar
- Küçük şifreleme üssü (örn.
= 3) kullanıldığında şifrelenen
mesajı da küçükse
,
değeri
’den küçük bir değere karşılık gelir. Bu durumda şifreli mesajlar tam sayılardaki
dereceden kökleri alınarak kolayca çözülebilirler.
- Eğer bir mesaj aynı şifreleme üssü
ve farklı
değerleri ile birden çok kişiye gönderiliyorsa, bu mesaj kullanılarak kolayca çözülebilir.
- RSA algoritması herhangi bir rastsallık içermediği için bazı düz mesajlar şifrelenip herhangi bir şifreli mesaja eşit olup olmadığı kontrol edilebilir. Dolayısıyla dolgu kullanılmayan RSA anlamsal güvenliğe sahip değildir.
- RSA yönteminde iki şifreli mesajın çarpımı, kendilerine karşılık gelen düz mesajların çarpımının şifrelenmiş haline eşittir. Yani,
Bu çarpımsal özelliğinden dolayı RSA’e seçilmiş şifreli mesaj atağı gerçekleştirilebilir. Örneğin, bir şifreli mesaj olan
'nin çözümünü elde etmek isteye bir saldırgan rastgele bir
değeri seçip, özel anahtara sahip kişiye şüpheli gözükmeyen
mesajını gönderip deşifre etmesini isteyebilir. Çarpımsal özellikten dolayı
,
'in şifreli halidir. Eğer saldırgan atakta başarılı olursa
değerini elde eder ve
ile çarpıp kolayca m değerini bulur.
Dolgu Şemaları
Tüm bu problemleri ortadan kaldırmak için kullanılan RSA uygulamaları şifrelemeden önce düz mesaj olan 
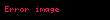
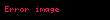
Mesaj İmzalama
RSA ayrıca mesajları imzalamak için de kullanılabilir. Alice’in Bob’a imzalanmış bir mesaj göndermek istediğini düşünelim. Alice kendi özel anahtarını kullanarak bunu gerçekleştirebilir. Mesajın özet değerini hesaplayıp mod 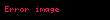

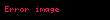

Doğruluk İspatları
Fermat’nın Küçük Teoremi ile İspatı
Fermat'nın küçük teoremi 



Her 
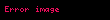
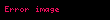


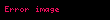
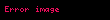
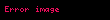
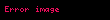
med 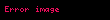
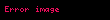
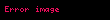
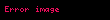
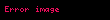
.
med 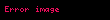
Euler teoremi ile ispatı
Rivest, Shamir ve Adleman orijinal makalelerinde RSA yönteminin çalışmasını açıklarken Fermat’nın küçük teoremini kullanmalarına rağmen genellikle ispatlarda Euler teoremi kullanılır.
Her 
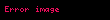
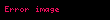
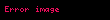
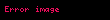

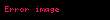
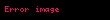


Son eşitlik Euler teoremi’nin bir sonucudur. Eğer 

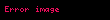
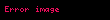
RSA algoritması
RSA çok büyük tam sayılarla işlem yapmanın zorluğuna dayanan bir tekniktir. Yani, RSA algoritmasını kullanan kişi 2 büyük asal sayı seçer ve bunları saklar. Bu iki asal sayının çarpımı elde edip, rastgele seçtiği başka bir değer ile birlikte ortak anahtar olarak belirler. Ortak anahtarı kullanan başka bir kullanıcı şifreleme yapabilir bu durumda bu mesajın şifresinin çözülüp anlamlı hale getirilebilmesi için ortak anahtar yeterince büyük olduğundan bu büyük sayının ortak çarpanlarının bilinmesi gerekir. Yani aslında RSA çarpanlara ayırma ile birebir ilişkilidir ki bu algoritma açık anahtarlı şifrelemeyi kullanır. Açık anahtarlı şifrelemede (asimetrik şifreleme) açık anahtarla şifreleme ve gizli anahtarla deşifreleme yapılmasını kolayca gerçekleştirilirken; yalnızca açık anahtarı (iki sayının çarpımını) bilerek gizli anahtarın bulunmasını zor kılar (büyük olan bu sayının çarpanlarının bilinmesi gerekir). RSA 3 basamakta gerçekleştirilir. Bunlar: anahtar üretimi (2 büyük asal sayının çarpımı ve random seçilmiş bir sayı ile ortak anahtar üretilmesi), şifreleme (Oluşan ortak anahtarı kullanan başka bir kullanıcı şifreleme yapabilir) ve şifre çözmedir (Şifrenin çözülmesi için ortak anahtarın çarpanlarının bilinmesi gerekir). Özet olarak; tamamen random olarak ve birbirine yakın iki asal sayı seçilir. Bu sayılar tutulur. Mod n olacak şekilde ; n=p*q ve m(=(p-1)*(q-1) çarpımları hesaplanır. 1<e<m arasında bir e tam sayısı seçilir. Öyle ki e ve m’nin en büyük ortak böleni 1 olsun. Genel üs olarak kullandığımız e ve m sayıları kullanılarak gizli üs d hesaplanır (1<d<m) (Örneğin ed≡1(mod m)). Genel anahtar (n,e) ve özel anahtar (n,d)’dir. p,q ve m değerleri de gizli tutulmalıdır. .NET framework teknolojisinde kullanan RSA algoritmasına bakacak olursak:
byte[] dataToEncrypt = ByteConverter.GetBytes("Sifrelenecek Veri"); Şifrelenmiş ve deşifrelenmiş olan verilerin tutulduğu veri tanımları yapılır.
byte[] encryptedData; byte[] decryptedData;
1024 uzunluğunda RSACryptoServiceProvider sınıfından nesne üretilir.
RSACryptoServiceProvider RSAalg = new RSACryptoServiceProvider(1024);
Aşağıdaki RSAEncrypt metodu veriyi şifrelemeyi sağlar. Metottaki ilk parametre şifrelenecek veridir. Byte array şeklindedir. Metottaki ikinci parametre (RSAalg.ExportParameters(false)) anahtar bilgisinin dışa verilip verilmeyeceğini ifade eder. False olarak değer atanmışsa public anahtar dışa verilir, true olarak değer atanmışsa public ve private anahtarlar dışa verilir. Kodumuzda false olarak değer atandığı için sadece public anahtar dışa verilir. Metottaki üçüncü parametre boolean bir değerdir. Padding mode olarak isimlendirilir. Padding boolean değerinin kullanılması gereklidir çünkü metoda gönderilen verinin şifrelenecek verinin tamamının olup olmadığını bu flag değerinden anlarız. Şifrelenecek veri çok büyük boyutlarda olabilir bu da verinin bloklara bölünmesini gerektirir. Bloklara bölünen verinin tamamının şifrelendiği bu flag değerden anlaşılır. Eğer padding değeri true ise bu halde gelişmiş OAEP 16 kullanılır. Aksi takdirde geleneksel PKCS 1 v1.5 kullanılır.
encryptedData = RSAEncrypt(dataToEncrypt,RSAalg.ExportParameters(false), false);
Aşağıdaki decryptedData metodu veriyi deşifrelemeye sağlar. Metottaki ilk parametre deşifrelenecek veridir. Byte array şeklindedir. Metottaki ikinci parametre (RSAalg.ExportParameters(true))anahtar bilgisinin dışa verilip verilmeyeceğini ifade eder. False olarak değer atanmışsa public anahtar dışa verilir, true olarak değer atanmışsa public ve private anahtarlar dışa verilir. Kodumuzda true olarak değer atandığı için private ve public anahtar dışa verilir. Metottaki üçüncü parametre boolean bir değerdir. Padding mode olarak isimlendirilir. Padding boolean değerinin kullanılması gereklidir çünkü metoda gönderilen verinin şifrelenecek verinin tamamının olup olmadığını bu flag değerinden anlarız. Şifrelenecek veri çok büyük boyutlarda olabilir bu da verinin bloklara bölünmesini gerektirir. Bloklara bölünen verinin tamamının şifrelendiği bu flag değerden anlaşılır. Eğer padding değeri true ise bu halde gelişmiş OAEP 16 kullanılır. Aksi takdirde geleneksel PKCS 1 v1.5 kullanılır.
decryptedData = RSADecrypt(encryptedData,RSAalg.ExportParameters(true), false);
Kaynakça
- ^ a b MOLLIN, RICHARD A. (2019). Rsa And Publıc-Key Cryptography. [S.l.]: CRC PRESS. ISBN . OCLC 1112201971.
- ^ a b Prodhan, Georgina (4 Ekim 2010). "Secret coding inventors finally win recognition". Reuters (İngilizce). 13 Ocak 2021 tarihinde kaynağından . Erişim tarihi: 11 Ocak 2021.
- ^ dotnet-bot. . docs.microsoft.com (İngilizce). 31 Aralık 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Ocak 2021.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddedeki bilgilerin dogrulanabilmesi icin ek kaynaklar gerekli Lutfen guvenilir kaynaklar ekleyerek maddenin gelistirilmesine yardimci olun Kaynaksiz icerik itiraz konusu olabilir ve kaldirilabilir Kaynak ara RSA sifreleme yonetimi haber gazete kitap akademik JSTOR Kasim 2023 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin RSA guvenligi tam sayilari carpanlarina ayirmanin algoritmik zorluguna dayanan bir tur acik anahtarli sifreleme yontemidir 1978 de Ron Rivest Adi Shamir ve Leonard Adleman tarafindan bulunmustur Bir RSA kullanicisi iki buyuk asal sayinin carpimini uretir ve sectigi diger bir degerle birlikte ortak anahtar olarak ilan eder Secilen asal carpanlari ise saklar Ortak anahtari kullanan biri herhangi bir mesaji sifreleyebilir ancak su anki yontemlerle eger ortak anahtar yeterince buyukse sadece asal carpanlari bilen kisi bu mesaji cozebilir RSA sifrelemeyi kirmanin carpanlara ayirma problemini kirmak kadar zor olup olmadigi hala kesinlesmemis bir problemdir TarihiBirlesik Krallik haber alma teskilati GCHQ da calisan Ingiliz matematikci 1973 te kurum ici bir dokumanda esdeger bir sistemi acikladi Fakat bu sistemi hayata gecirmek icin epeyce pahali bilgisayarlarin kullanilmasi gerekiyordu ve bilindigi kadariyla hic kullanilmadi Fakat Cocks un bulusu 1998 e kadar cok gizli oldugu gerekcesiyle aciga cikarilmadi Rivest Shamir ve Adleman RSA yontemini Cocks un calismasindan bagimsiz olarak tasarladilar RSA algoritmasi 1978 de MIT de Ron Rivest Adi Shamir ve Leonard Adleman tarafindan aciklandi RSA harfleri soyisimlerinin bas harflerini temsil etmektedir PatentMIT e 20 Eylul 1983 te algoritmayi kullanan bir Sifreleme iletisim sistemi ve yontemi icin ABD Patenti 4 405 829 verildi Patent 21 Eylul 2000 de sona erecek olsa da patent suresi 17 yildir algoritma iki hafta once 6 Eylul 2000 de RSA Security tarafindan kamuya aciklandi Algoritmanin ayrintili bir aciklamasi Scientific American in Agustos 1977 sayisinda Matematik Oyunlari sutununda yayinlandigindan patent basvurusunun Aralik 1977 dosyalama tarihinden once dunyanin geri kalaninin cogunda duzenlemeler baska yerlerde ve sadece ABD patenti verildi Cocks un calismalari herkes tarafindan biliniyor olsaydi ABD deki bir patent de yasal olmayacakti nin patent ozetinden Sistem bir kodlama cihazina sahip en az bir terminale ve bir kod cozme cihazina sahip en az bir terminale baglanmis bir iletisim kanali icerir Aktarilacak bir mesaj onceden belirlenmis bir kumede M sayisi olarak kodlanarak kodlama terminalindeki sifreli metne sifrelenir Bu sayi daha sonra onceden belirlenmis bir guce istenen alici ile iliskili yukseltilir ve son olarak hesaplanir Kalan veya kalinti C ussel sayi onceden belirlenmis iki asal sayinin carpimina hedeflenen alici ile iliskili bolundugunde hesaplanir IslemlerRSA algoritmasi anahtar uretimi sifreleme ve sifre cozme olmak uzere 3 basamaktan olusmaktadir Anahtar Uretimi RSA icin bir ortak anahtar bir de ozel anahtar gerekir Ortak anahtar herkes tarafindan bilinir ve mesaji sifrelemek icin kullanilir Bir ortak anahtarla sifrelenmis mesaj sadece ozel anahtarla cozulebilir RSA anahtarlari su sekilde olusturulur Iki adet birbirinden degisik asal sayi secin bunlarin adini da p displaystyle p ve q displaystyle q koyalim Guvenlik amaciyla p ve q sayilari rastgele secilmeli ve yakin uzunlukta olmalidirlar Bu sayilar asallik testi kullanilarak etkin bir sekilde bulunabilir n pq displaystyle n pq hesaplayin n displaystyle n ozel ve ortak anahtarlar icin mod degeri olarak kullanilacaktir Bu sayilarin totienti olan f n p 1 q 1 displaystyle varphi n p 1 q 1 hesaplayin Bir tam sayi uretin ve adini da e displaystyle e koyun Bu sayi 1 lt e lt f n displaystyle 1 lt e lt varphi n kosuluna uygun olmali ve f n displaystyle varphi n ile en buyuk ortak boleni 1 olmalidir baska bir deyisle f n displaystyle varphi n ve e displaystyle e kendi aralarinda asal olmalidir e displaystyle e ortak anahtar olarak aciklanir Bit uzunlugu kisa olan ve kucuk sahip e displaystyle e degerleri yaygin olarak 0x10001 65 537 daha verimli sifreleme saglarlar Fakat kucuk e displaystyle e degerleri ornegin 3 bazi durumlarda guvenligi azaltabilir de 1 modf n displaystyle de equiv 1 pmod varphi n olacak sekilde bir d displaystyle d yi belirleyin d displaystyle d ozel anahtar ussu olarak saklanir d displaystyle d degeri genellikle kullanilarak hesaplanir Ortak anahtar mod degeri olan n displaystyle n den ve ortak us olan e displaystyle e den olusur Ozel anahtar ise mod degeri olan n displaystyle n den ve ozel us olan ve gizli kalmasi gereken d displaystyle d den olusur p displaystyle p q displaystyle q ve f n displaystyle varphi n degerleri de gizli kalmalidir cunku d displaystyle d yi hesaplamada kullanilirlar Sifreleme Alice ortak anahtari n displaystyle n e displaystyle e yi Bob a gonderir ozel anahtarini gizli tutar Bob M displaystyle M mesajini Alice e gondermek istedigi zaman ilk olarak M displaystyle M yi ters cevrilebilir bir protokol ile dolgu semasi 0 lt m lt n displaystyle 0 lt m lt n olacak sekilde bir m displaystyle m tam sayisina donusturur Daha sonra sifrelenmis mesaj c displaystyle c yi c me mod n displaystyle c m e text mod n text olacak sekilde hesaplar Bunu karesini alarak us alma yontemiyle hizli bir sekilde hesaplayabilir Bob c displaystyle c yi Alice e iletir Sifre Cozme Alice m displaystyle m mesajini ozel anahtari olan d displaystyle d yi kullanarak sifreli mesaj c displaystyle c den su sekilde hesaplar m cd mod n displaystyle m c d text mod n text Alice m displaystyle m yi bulduktan sonra dolgu semasinin tersini alarak orijinal mesaj M displaystyle M yi elde eder Ornek Iki farkli asal sayi secelim p 61 displaystyle p 61 ve q 53 displaystyle q 53 olsun n pq displaystyle n pq degerini hesaplayalim 61 53 3233 Totient degerini hesaplayalim f 3233 61 1 53 1 3120 displaystyle varphi 3233 61 1 53 1 3120 1 ile 3120 arasinda 3120 ile aralarinda asal olan bir e displaystyle e degeri secelim e displaystyle e degerini asal secersek sadece 3120 nin boleni olup olmadigini kontrol etmemiz gerekir e 17 displaystyle e 17 olsun d displaystyle d yi e displaystyle e nin mod f n displaystyle varphi n deki carpmaya gore tersi olarak hesaplayalim d 2753 displaystyle d 2753 Ortak Anahtar n 3233 e 17 displaystyle n 3233 e 17 Herhangi bir m displaystyle m mesaji icin sifreleme fonksiyonu m17 displaystyle m 17 mod 3233 Ozel Anahtar n 3233 d 2753 displaystyle n 3233 d 2753 Herhangi bir c displaystyle c sifreli mesaji icin sifre cozme fonksiyonu c2753 displaystyle c 2753 mod 3233 Ornegin m 65 displaystyle m 65 i su sekilde sifreleriz c 6517 mod 3233 2790 displaystyle c 65 17 text mod 3233 text 2790 c 2790 displaystyle c 2790 in su sekilde sifresini cozebiliriz m 27902753 mod 3233 65 displaystyle m 2790 2753 text mod 3233 text 65 Tum bu hesaplamalar karesini alarak us alma yontemiyle hizli bir sekilde gerceklestirilebilir Duz RSA karsisindaki Saldirilar Kucuk sifreleme ussu orn e displaystyle e 3 kullanildiginda sifrelenen m displaystyle m mesaji da kucukse m lt n1 e displaystyle m lt n 1 e me displaystyle m e degeri n displaystyle n den kucuk bir degere karsilik gelir Bu durumda sifreli mesajlar tam sayilardaki e displaystyle e dereceden kokleri alinarak kolayca cozulebilirler Eger bir mesaj ayni sifreleme ussu e displaystyle e ve farkli n displaystyle n degerleri ile birden cok kisiye gonderiliyorsa bu mesaj kullanilarak kolayca cozulebilir RSA algoritmasi herhangi bir rastsallik icermedigi icin bazi duz mesajlar sifrelenip herhangi bir sifreli mesaja esit olup olmadigi kontrol edilebilir Dolayisiyla dolgu kullanilmayan RSA anlamsal guvenlige sahip degildir RSA yonteminde iki sifreli mesajin carpimi kendilerine karsilik gelen duz mesajlarin carpiminin sifrelenmis haline esittir Yani m1em2e m1m2 e mod n displaystyle m 1 e m 2 e equiv m 1 m 2 e text mod n text Bu carpimsal ozelliginden dolayi RSA e secilmis sifreli mesaj atagi gerceklestirilebilir Ornegin bir sifreli mesaj olan c me mod n displaystyle c m e text mod n text nin cozumunu elde etmek isteye bir saldirgan rastgele bir r displaystyle r degeri secip ozel anahtara sahip kisiye supheli gozukmeyen c cre mod n displaystyle c cr e text mod n text mesajini gonderip desifre etmesini isteyebilir Carpimsal ozellikten dolayi c displaystyle c mr mod n displaystyle mr text mod n text in sifreli halidir Eger saldirgan atakta basarili olursa mr mod n displaystyle mr text mod n text degerini elde eder ve r 1 displaystyle r 1 ile carpip kolayca m degerini bulur Dolgu Semalari Tum bu problemleri ortadan kaldirmak icin kullanilan RSA uygulamalari sifrelemeden once duz mesaj olan m displaystyle m ye rastsallastirilmis uygularlar Bu dolgu n displaystyle n yi guvensiz duz metin araliginda olmaktan korur ve n displaystyle n in sabit bir sifreli mesaji olmasini engeller Dolgulama icin tasarlanan PKCS 1 standardinin ilk versiyonlarinin adaptif secilmis sifreli mesaj atagina karsi dayaniksizligi ortaya cikinca sonraki versiyonlar bu atagi engellemek icin OAEP icermekteler Mesaj Imzalama RSA ayrica mesajlari imzalamak icin de kullanilabilir Alice in Bob a imzalanmis bir mesaj gondermek istedigini dusunelim Alice kendi ozel anahtarini kullanarak bunu gerceklestirebilir Mesajin ozet degerini hesaplayip mod n displaystyle n de d displaystyle d kuvvetini alir ve imza olarak mesaja ilistirir Bob mesaji aldigi zaman ayni ozetleme algoritmasiyla mesajin ozetini hesaplar Bob ayrica mesajin imzasinin mod n displaystyle n de e displaystyle e kuvvetini alir ve mesajin ozetiyle karsilastirir Eger iki deger birbirine esitse mesajin Alice den geldigini anlar RSA ile imza gerceklestirilirken de gibi guvenli dolgu semalari kullanilmasi gereklidir Ayrica guvenlik acisinda sifrelemede ve imzada ayni anahtar kullanilmamalidir Dogruluk IspatlariFermat nin Kucuk Teoremi ile Ispati Fermat nin kucuk teoremi p displaystyle p asali ve p displaystyle p nin bolmedigi bir a displaystyle a tam sayisi icin a p 1 1 mod p displaystyle a p 1 equiv 1 text mod p text denkliginin dogru oldugunu belirtir Her m displaystyle m mesaji icin me d displaystyle equiv m modpq displaystyle bmod p q denkliginin dogru oldugunu gostermek istiyoruz ed 1 mod p 1 q 1 displaystyle ed equiv 1 text mod p 1 q 1 text oldugunu biliyoruz Yani negatif olmayan bir p displaystyle p tam sayisi icin ed 1 h p 1 q 1 displaystyle ed 1 h p 1 q 1 yazabiliriz Eger med displaystyle equiv m mod p ve med displaystyle equiv m mod q oldugunu gosterirsek med displaystyle equiv m mod pq oldugunu ispatlamis oluruz med displaystyle equiv m mod p oldugunu gostermek icin m displaystyle equiv 0 mod p ve m displaystyle not equiv 0 mod p durumlarina bakalim Ilk durumda med p nin kati oldugundan med displaystyle equiv 0 displaystyle equiv m mod p Ikinci durumda da mp 1 in Fermat nin kucuk teoreminden dolayi 1 e denk olmasini kullanarak ispati yapabiliriz med m ed 1 m mh p 1 q 1 m mp 1 h q 1 m 1h q 1 m m mod p displaystyle m ed m ed 1 m m h p 1 q 1 m m p 1 h q 1 m equiv 1 h q 1 m equiv m text mod p text med displaystyle equiv m mod q oldugunu da benzer sekilde gosterip algoritmanin dogrulugunu ispatlamis oluruz Euler teoremi ile ispati Rivest Shamir ve Adleman orijinal makalelerinde RSA yonteminin calismasini aciklarken Fermat nin kucuk teoremini kullanmalarina ragmen genellikle ispatlarda Euler teoremi kullanilir Her m displaystyle m mesaji icin me d displaystyle equiv m modpq displaystyle bmod p q denkliginin dogru oldugunu gostermek istiyoruz ed displaystyle equiv 1 mod f n displaystyle varphi n oldugunu biliyoruz Dolayisiyla negatif olmayan bir h displaystyle h tam sayisi icin ed displaystyle ed carpimini ed 1 hf n displaystyle ed 1 h varphi n seklinde yazabiliriz m displaystyle m ve n displaystyle n nin aralarinda asal oldugunu varsayarsak med m1 hf n m mf n h m mod n displaystyle m ed equiv m 1 h varphi n equiv m m varphi n h equiv m text mod n text Son esitlik Euler teoremi nin bir sonucudur Eger m displaystyle m ve n displaystyle n aralarinda asal degilse bu arguman dogru olmaz m displaystyle equiv 0 mod p vem displaystyle equiv 0 mod q durumlari yukaridaki ispatta oldugu gibi gosterilebilir RSA algoritmasiRSA cok buyuk tam sayilarla islem yapmanin zorluguna dayanan bir tekniktir Yani RSA algoritmasini kullanan kisi 2 buyuk asal sayi secer ve bunlari saklar Bu iki asal sayinin carpimi elde edip rastgele sectigi baska bir deger ile birlikte ortak anahtar olarak belirler Ortak anahtari kullanan baska bir kullanici sifreleme yapabilir bu durumda bu mesajin sifresinin cozulup anlamli hale getirilebilmesi icin ortak anahtar yeterince buyuk oldugundan bu buyuk sayinin ortak carpanlarinin bilinmesi gerekir Yani aslinda RSA carpanlara ayirma ile birebir iliskilidir ki bu algoritma acik anahtarli sifrelemeyi kullanir Acik anahtarli sifrelemede asimetrik sifreleme acik anahtarla sifreleme ve gizli anahtarla desifreleme yapilmasini kolayca gerceklestirilirken yalnizca acik anahtari iki sayinin carpimini bilerek gizli anahtarin bulunmasini zor kilar buyuk olan bu sayinin carpanlarinin bilinmesi gerekir RSA 3 basamakta gerceklestirilir Bunlar anahtar uretimi 2 buyuk asal sayinin carpimi ve random secilmis bir sayi ile ortak anahtar uretilmesi sifreleme Olusan ortak anahtari kullanan baska bir kullanici sifreleme yapabilir ve sifre cozmedir Sifrenin cozulmesi icin ortak anahtarin carpanlarinin bilinmesi gerekir Ozet olarak tamamen random olarak ve birbirine yakin iki asal sayi secilir Bu sayilar tutulur Mod n olacak sekilde n p q ve m p 1 q 1 carpimlari hesaplanir 1 lt e lt m arasinda bir e tam sayisi secilir Oyle ki e ve m nin en buyuk ortak boleni 1 olsun Genel us olarak kullandigimiz e ve m sayilari kullanilarak gizli us d hesaplanir 1 lt d lt m Ornegin ed 1 mod m Genel anahtar n e ve ozel anahtar n d dir p q ve m degerleri de gizli tutulmalidir NET framework teknolojisinde kullanan RSA algoritmasina bakacak olursak byte dataToEncrypt ByteConverter GetBytes Sifrelenecek Veri Sifrelenmis ve desifrelenmis olan verilerin tutuldugu veri tanimlari yapilir byte encryptedData byte decryptedData 1024 uzunlugunda RSACryptoServiceProvider sinifindan nesne uretilir RSACryptoServiceProvider RSAalg new RSACryptoServiceProvider 1024 Asagidaki RSAEncrypt metodu veriyi sifrelemeyi saglar Metottaki ilk parametre sifrelenecek veridir Byte array seklindedir Metottaki ikinci parametre RSAalg ExportParameters false anahtar bilgisinin disa verilip verilmeyecegini ifade eder False olarak deger atanmissa public anahtar disa verilir true olarak deger atanmissa public ve private anahtarlar disa verilir Kodumuzda false olarak deger atandigi icin sadece public anahtar disa verilir Metottaki ucuncu parametre boolean bir degerdir Padding mode olarak isimlendirilir Padding boolean degerinin kullanilmasi gereklidir cunku metoda gonderilen verinin sifrelenecek verinin tamaminin olup olmadigini bu flag degerinden anlariz Sifrelenecek veri cok buyuk boyutlarda olabilir bu da verinin bloklara bolunmesini gerektirir Bloklara bolunen verinin tamaminin sifrelendigi bu flag degerden anlasilir Eger padding degeri true ise bu halde gelismis OAEP 16 kullanilir Aksi takdirde geleneksel PKCS 1 v1 5 kullanilir encryptedData RSAEncrypt dataToEncrypt RSAalg ExportParameters false false Asagidaki decryptedData metodu veriyi desifrelemeye saglar Metottaki ilk parametre desifrelenecek veridir Byte array seklindedir Metottaki ikinci parametre RSAalg ExportParameters true anahtar bilgisinin disa verilip verilmeyecegini ifade eder False olarak deger atanmissa public anahtar disa verilir true olarak deger atanmissa public ve private anahtarlar disa verilir Kodumuzda true olarak deger atandigi icin private ve public anahtar disa verilir Metottaki ucuncu parametre boolean bir degerdir Padding mode olarak isimlendirilir Padding boolean degerinin kullanilmasi gereklidir cunku metoda gonderilen verinin sifrelenecek verinin tamaminin olup olmadigini bu flag degerinden anlariz Sifrelenecek veri cok buyuk boyutlarda olabilir bu da verinin bloklara bolunmesini gerektirir Bloklara bolunen verinin tamaminin sifrelendigi bu flag degerden anlasilir Eger padding degeri true ise bu halde gelismis OAEP 16 kullanilir Aksi takdirde geleneksel PKCS 1 v1 5 kullanilir decryptedData RSADecrypt encryptedData RSAalg ExportParameters true false Kaynakca a b MOLLIN RICHARD A 2019 Rsa And Public Key Cryptography S l CRC PRESS ISBN 0 367 39565 7 OCLC 1112201971 a b Prodhan Georgina 4 Ekim 2010 Secret coding inventors finally win recognition Reuters Ingilizce 13 Ocak 2021 tarihinde kaynagindan Erisim tarihi 11 Ocak 2021 dotnet bot docs microsoft com Ingilizce 31 Aralik 2018 tarihinde kaynagindan arsivlendi Erisim tarihi 11 Ocak 2021
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans