Radon–Nikodym teoremi

Matematikte Radon-Nikodym teoremi, aynı tanımlanmış iki ölçü arasındaki ilişkiyi ifade eden bir sonuçtur. Burada ölçü ile kastedilen ölçülebilir bir uzayın ölçülebilir alt kümelerine tutarlı bir büyüklük atayan bir küme fonksiyonudur. Ölçü örnekleri arasında alan ve hacim verilebilir.

Verilen bir ölçüyü yeni bir ölçüye dönüştürmenin bir yolu, uzayın her noktasına bir yoğunluk atamak ve ardından istenilen ölçülebilir alt küme üzerinde integral almaktır ve şu şekilde ifade edilebilir:

${\displaystyle \nu (A)=\int _{A}f\,d\mu .}$

Burada ν, ölçülebilir herhangi bir alt küme A için tanımlanan yeni ölçüdür. f fonksiyonu ise verilen bir noktadaki yoğunluktur. İntegral, μ ölçüsüne göre alınır ve bu ölçü genellikle gerçel doğru R üzerindeki veya n boyutlu Öklid uzayı Rⁿ'deki Lebesgue ölçüsüdür. Bu ölçü, uzunluk, alan ve hacim gibi standart kavramlara karşılık gelir. Örneğin, kütle yoğunluğu f ve üç boyutlu uzay R³'teki Lebesgue ölçüsü μ ile gösterilirse, o zaman ν(A) uzaysal bir bölge A'daki toplam kütleye eşit olacaktır.

Radon-Nikodym teoremi esasen, belirli koşullar altında, herhangi bir ν ölçüsünün aynı uzaydaki başka bir μ ölçüsüne göre bu şekilde ifade edilebileceğini belirtir.  f  fonksiyonu o zaman Radon-Nikodym türevi olarak adlandırılır ve ${\displaystyle {\tfrac {d\nu }{d\mu }}}$ şeklinde gösterilir. Radon-Nikodym teoreminin önemli bir uygulaması olasılık teorisinde görülür. Bu uygulamada, rassal bir değişkenin olasılık yoğunluk fonksiyonu elde edilir.

Teorem, bu sonucu 1913'te Rⁿ için kanıtlayan Johann Radon'un ve yine aynı sonucu daha bir genel durumda 1930'da kanıtlayan Otto Nikodym'in adını almıştır. 1936'da Hans Freudenthal, bugün Riesz uzay teorisinde bir sonuç olan kanıtlayarak Radon-Nikodym teoremini genelleştirdi. Bu sonuçta, Radon-Nikodym teoremi özel bir sonuç olarak elde edilir.

Y Banach uzayıysa ve Radon-Nikodym teoreminin genellemesi Y değerlerine sahip fonksiyonlar için de geçerliyse (mutatis mutandis), o zaman Y'nin Radon-Nikodym özelliğine sahip olduğu söylenir. Bütün Hilbert uzayları Radon-Nikodym özelliğine sahiptir.

Teoremin ifadesi

${\displaystyle (X,\Sigma )}$ , ${\displaystyle \mu }$ ve ${\displaystyle \nu }$ de bu uzayın üzerinde tanımlı olsun. Eğer ${\displaystyle \nu \ll \mu }$ ise (yani, ${\displaystyle \nu }$ ölçüsü ${\displaystyle \mu }$'ye göre ölçü ise), o zaman ölçülebilir herhangi bir ${\displaystyle A\in \Sigma }$ için $${\displaystyle \nu (A)=\int _{A}f\,d\mu .}$$ eşitliğini sağlayan ${\displaystyle \Sigma }$- bir ${\displaystyle f:X\to [0,\infty )}$ fonksiyonu vardır.

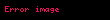
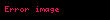
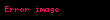
Radon-Nikodym türevi

Yukarıdaki eşitliği sağlayan ${\displaystyle f}$ fonksiyonu ${\displaystyle \mu }$'ye göre sıfır ölçülü kümeler haricinde biriciktir. Diğer deyişle, eğer aynı özelliği sağlayan başka bir ${\displaystyle g}$ fonksiyonu olsaydı, o zaman ${\displaystyle f}$ ile ${\displaystyle g}$ fonksiyonları ${\displaystyle \mu }$'ye göre birbirine eşit olurdu. Sonuç olarak, böyle bir ${\displaystyle f}$ fonksiyonu genelde ${\frac {d\nu }{d\mu }}$ olarak yazılır ve fonksiyona Radon–Nikodym türevi' denilir. Buradaki gösterim ve türev terimi kastidir; kalkülüsteki türeve benzeyecek şekilde bir ölçünün yoğunluğunun değişim oranının diğerininkine oranını gösterir.

İşaretli veya karmaşık ölçülere genelleştirilmesi

Benzer bir teorem ve için de kanıtlanabilir. Eğer ${\displaystyle \mu }$ negatif olmayan , ${\displaystyle \nu }$ sonlu-değer alan işaretli veya karmaşık bir ölçü ve ${\displaystyle \nu \ll \mu }$ ise, o zaman ${\displaystyle X}$ üzerinde tanımlı, gerçel veya karmaşık değerli,${\displaystyle \mu }$'ye göre integrali olan ve ölçülebilir herhangi bir ${\displaystyle A}$ için

$${\displaystyle \nu (A)=\int _{A}g\,d\mu }$$

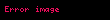
ilişkisini sağlayan bir ${\displaystyle g}$ fonksiyonu vardır.

Örnekler

Aşağıdaki örneklerde, X kümesi [0,1] aralığı, 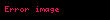${\displaystyle \Sigma }$ ise X üzerinde .

• ${\displaystyle \mu }$, X üzerinde tanımlı uzunluk ölçüsü olsun. ${\displaystyle \nu }$ ise X'in altkümesi Y'ye Y'nin uzunluğunun iki katını atasın. O zaman, ${\textstyle {\frac {d\nu }{d\mu }}=2}$.
• ${\displaystyle \mu }$, X üzerinde tanımlı uzunluk ölçüsü olsun. ${\displaystyle \nu }$ ise X'in altkümesi Y'ye {0.1, …, 0.9} kümesinin Y içinde olan eleman sayısını atasın. O zaman, ${\displaystyle \nu }$ ölçüsü ${\displaystyle \mu }$'ye göre mutlak sürekli değildir; çünkü, ${\displaystyle \nu }$ ölçüsü, ${\displaystyle \mu }$'ye göre ölçüsü sıfır olan noktalar kümesine sıfır olmayan ölçü değerleri tayin etmektedir. Gerçekten de, ${\textstyle {\frac {d\nu }{d\mu }}}$ türevi yoktur. Mesela, herhangi bir ${\displaystyle \varepsilon >0}$ için, ${\displaystyle (0.1-\varepsilon )}$'den ${\displaystyle (0.1+\varepsilon )}$'a kadar integrali 1 olan sonlu bir fonksiyon yoktur.
• ${\displaystyle \nu }$ ölçüsü X üzerinde tanımlı uzunluk ölçüsü, ${\displaystyle \delta _{0}}$ ölçüsü 0 merkezli (0'ı içeren herhangi bir kümenin ölçüsü 1, geri kalan kümelerin ölçüsü ise 0) ve son olarak ${\displaystyle \mu =\nu +\delta _{0}}$ olsun. O zaman, ${\displaystyle \nu }$ ölçüsü ${\displaystyle \mu }$'ye göre mutlak süreklidir ve ${\textstyle {\frac {d\nu }{d\mu }}=1_{X\setminus \{0\}}}$ olur. Yani, ${\displaystyle x=0}$'da türev 0, ${\displaystyle x>0}$ olduğunda ise türev 1 olur.

Özellikler

• ν, μ ve λ aynı ölçülebilir uzayda σ-sonlu ölçü olsunlar. Eğer ν ≪ λ ve μ ≪ λ (hem ν hem de μ, λ 'ya göre mutlak sürekli) ise, o zaman λ'ya göre hemen hemen her yerde

$${\displaystyle {\frac {d(\nu +\mu )}{d\lambda }}={\frac {d\nu }{d\lambda }}+{\frac {d\mu }{d\lambda }}}$$

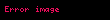
olur.

• Eğer ν ≪ μ ≪ λ ise, o zaman λ'ya göre hemen hemen her yerde

$${\displaystyle {\frac {d\nu }{d\lambda }}={\frac {d\nu }{d\mu }}{\frac {d\mu }{d\lambda }}}$$

olur. Bilhassa, μ ≪ ν ve ν ≪ μ ise, o zaman ν'ye göre hemen hemen her yerde

$${\displaystyle {\frac {d\mu }{d\nu }}=\left({\frac {d\nu }{d\mu }}\right)^{-1}}$$ olur.

• μ ≪ λ ise ve g fonksiyonun μ'ye göre integrali varsa, o zaman

$${\displaystyle \int _{X}g\,d\mu =\int _{X}g{\frac {d\mu }{d\lambda }}\,d\lambda .}$$

• ν sonlu işaretli veya karmaşık ölçü ise, o zaman $${\displaystyle {d|\nu | \over d\mu }=\left|{d\nu \over d\mu }\right|.}$$

Uygulamalar

Olasılık teorisi

Teorem, olasılık teorisinin fikirlerini gerçel sayılar üzerinde tanımlanan olasılık kütle ve yoğunluk fonksiyonlarından keyfi kümeler üzerinde tanımlanan genişletmede çok önemlidir. Bir olasılık ölçüsünden diğerine geçmenin mümkün olup olmadığını ve nasıl mümkün olduğunu söyler. Örneğin, olasılık ölçüleri için koşullu beklentinin varlığını kanıtlamak için kullanılabilir.

Matematiksel finans

Diğer alanların yanı sıra, teorem, matematiksel finansta özellikle Girsanov teoremi aracılığıyla yaygın olarak kullanılır. Bu tür ölçü değişiklikleri, türevlerin adil fiyatlandırılmasının temel taşıdır ve gerçek dünyada gözlemlenmiş olasılıkları dönüştürmek için kullanılır.

Bilgi ıraksaklıkları

μ ve ν X üzerinde ölçü olsun. μ ≪ ν ise

• ν 'den μ 'ye $${\displaystyle D_{\text{KL}}(\mu \parallel \nu )=\int _{X}\log \left({\frac {d\mu }{d\nu }}\right)\;d\mu }$$

olarak tanımlanır.

• α > 0 ve α ≠ 1 için, ν 'den μ 'ye α mertebeden $${\displaystyle D_{\alpha }(\mu \parallel \nu )={\frac {1}{\alpha -1}}\log \left(\int _{X}\left({\frac {d\mu }{d\nu }}\right)^{\alpha -1}\;d\mu \right)}$$

olarak tanımlanır.

σ-sonluluk varsayımının gerekliliği

μ'nün σ-sonlu olmadığı ve Radon-Nikodym teoreminin geçerli olmadığı bir örnek verelim. Gerçel sayılar üzerinde ele alalım. Bir Borel kümesi A'nın μ, eğer A sonlu ise A'nın eleman sayısını verir; aksi takdirde, A'nın sayma ölçüsü ∞ olur. μ'nün gerçekten bir ölçü olduğu kolaylıkla kontrol edilebilir. Ancak, μ, σ-sonlu değildir. Çünkü, sonlu kümelerin sayılabilir birleşimleri herhangi bir Borel kümesini vermeyebilir. Diğer deyişle, bu halde yazılamayacak Borel kümeleri vardır. ν'nün bu Borel cebiri üzerindeki olağan olduğunu varsayalım. O zaman, ν ölçüsü, μ'ye göre mutlak süreklidir. Çünkü bir A kümesi için μ(A) = 0 olması ancak A boş küme ise gerçekleşir; bu durumda ν(A) da zaten sıfırdır.

Şimdi, diyelim ki Radon–Nikodym teoremi bu durumda sağlansın. Yani, elimizde ölçülebilir bir f fonksiyonu vardır öyle ki

${\displaystyle \nu (A)=\int _{A}f\,d\mu }$

tüm Borel kümeleri için sağlanır. Bu halde, A'yı A = {a} gibi tek noktadan oluşan bir küme alırsak, yukarıdaki integral her a sayısı için

${\displaystyle 0=f(a)}$

verecektir. O zaman,  f  sıfır olur. Sonuç olarak, Lebesgue ölçüsü ν de sıfır olacaktır. Bu, bir çelişkidir.

Ayrıca bakınız

• Girsanov teoremi

Kaynakça

1. ^ Billingsley, Patrick (1995). Probability and Measure. Third. New York: John Wiley & Sons. ss. 419-427. ISBN . 
2. ^ (1930). "Sur une généralisation des intégrales de M. J. Radon" (PDF). Fundamenta Mathematicae (Fransızca). Cilt 15. ss. 131-179. JFM 56.0922.02. 9 Eylül 2016 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 30 Ocak 2018. 
3. ^ (1996). Introduction to Operator Theory in Riesz Spaces. . ISBN . 
4. ^ "Calculating Radon Nikodym derivative". Stack Exchange. 7 Nisan 2018. Arşivlenmesi gereken bağlantıya sahip kaynak şablonu içeren maddeler ()