Rayleigh sayısı

Akışkanlar mekaniğinde, Rayleigh sayısı (Ra, Lord Rayleigh'e ithafen) bir akışkan için kaldırma kuvveti ilişkili bir boyutsuz sayıdır. Bu sayı, akışkanın akış rejimini karakterize eder: belirli bir alt aralıkta bir değer laminer akışı belirtirken, daha yüksek bir aralıktaki değer türbülanslı akışı belirtir. Belirli bir kritik değerin altında, akışkan hareketi olmaz ve ısı transferi konveksiyon yerine ısı iletimi ile gerçekleşir. Çoğu mühendislik uygulaması için Rayleigh sayısı büyük olup, yaklaşık 10⁶ ile 10⁸ arasında bir değerdedir.

Rayleigh sayısı, bir akışkandaki kaldırma kuvveti ve viskozite arasındaki ilişkiyi tanımlayan Grashof sayısı (Gr) ile momentum yayınımı ve arasındaki ilişkiyi tanımlayan Prandtl sayısının (Pr) çarpımı olarak tanımlanır: Ra = Gr × Pr. Bu nedenle, kaldırma kuvveti ve viskozite kuvvetlerinin oranı ile momentum ve termal yayınım oranının çarpımı olarak da değerlendirilebilir: Ra = B/μ × ν/α. Rayleigh sayısı, Nusselt sayısı (Nu) ile yakından ilişkilidir.

Türetim

Rayleigh sayısı, akışkanların (örneğin su veya hava) kütle yoğunluğunun homojen olmadığı durumlarda davranışını tanımlar. Kütle yoğunluğu farkları genellikle sıcaklık farklarından kaynaklanır. Tipik olarak bir akışkan ısındıkça genleşir ve daha az yoğun hale gelir. Yerçekimi, akışkanın daha yoğun kısımlarının batmasına neden olur, bu olaya konveksiyon denir. Lord Rayleigh, fenomenini incelemiştir. Rayleigh sayısı, Ra, bir akışkan için kritik bir değerin altında olduğunda, akış olmaz ve ısı transferi tamamen iletim yoluyla gerçekleşir; bu değeri aştığında ise ısı, doğal konveksiyonla taşınır.

Kütle yoğunluğu farkı sıcaklık farkından kaynaklandığında, Ra, difüzif ısıl taşınım zaman ölçeğinin hız ${\displaystyle u}$ ile konvektif ısıl taşınım zaman ölçeğine oranı olarak tanımlanır:

$${\displaystyle \mathrm {Ra} ={\frac {\text{ısı iletim yoluyla taşınım için zaman ölçeği}}{{\text{hız}}~u{\text{ ile konveksiyon yoluyla ısıl taşınım zaman ölçeği}}}}.}$$

Bu, Rayleigh sayısının bir tür Péclet sayısı olduğunu ifade eder. Üç boyutta da, 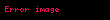${\displaystyle l}$ büyüklüğünde izotropik bir akışkan hacmi ve kütle yoğunluğu farkı ${\displaystyle \Delta \rho }$ için, yerçekimi kuvveti ${\displaystyle \Delta \rho l^{3}g}$ mertebesindedir; burada ${\displaystyle g}$, yerçekimi ivmesidir. göre, akışkan hacmi battığında, viskoz direnç ${\displaystyle \eta lu}$ mertebesindedir; burada ${\displaystyle \eta }$, akışkanın dinamik viskozitesidir. Bu iki kuvvet eşit olduğunda, hız ${\displaystyle u\sim \Delta \rho l^{2}g/\eta }$ olur. Dolayısıyla, akış yoluyla taşınımın zaman ölçeği ${\displaystyle l/u\sim \eta /\Delta \rho lg}$ olur. Bir mesafe boyunca termal difüzyonun zaman ölçeği ${\displaystyle l^{2}/\alpha }$ olup, burada ${\displaystyle \alpha }$, katsayısıdır. Böylece Rayleigh sayısı Ra şu şekilde ifade edilir:

$${\displaystyle \mathrm {Ra} ={\frac {l^{2}/\alpha }{\eta /\Delta \rho lg}}={\frac {\Delta \rho l^{3}g}{\eta \alpha }}={\frac {\rho \beta \Delta Tl^{3}g}{\eta \alpha }}}$$

burada, ortalama kütle yoğunluğu ${\displaystyle \rho }$ olan bir akışkan için yoğunluk farkı ${\displaystyle \Delta \rho =\rho \beta \Delta T}$ olarak ifade edilmiştir, Isıl genleşme katsayısı ${\displaystyle \beta }$ ve mesafe boyunca sıcaklık farkı ${\displaystyle \Delta T}$ ${\displaystyle l}$ olarak alınmıştır.

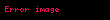
Rayleigh sayısı, Grashof sayısı ve Prandtl sayısının çarpımı olarak yazılabilir:

$${\displaystyle \mathrm {Ra} =\mathrm {Gr} \mathrm {Pr} .}$$

Klasik tanım

Dikey bir duvar yakınındaki için Rayleigh sayısı şu şekilde tanımlanır:

$${\displaystyle \mathrm {Ra} _{x}={\frac {g\beta }{\nu \alpha }}(T_{s}-T_{\infty })x^{3}=\mathrm {Gr} _{x}\mathrm {Pr} }$$

burada:

• x karakteristik uzunluktur
• Ra_x karakteristik uzunluk x için Rayleigh sayısıdır
• g yerçekimi ivmesidir
• β Isıl genleşme katsayısıdır (ideal gazlar için, T mutlak sıcaklık olmak üzere 1/T'ye eşittir).
• ${\displaystyle \nu }$
• α katsayısıdır
• T_s yüzey sıcaklığıdır
• T_∞ sakin sıcaklık (cismin yüzeyinden uzak akışkan sıcaklığı) olarak adlandırılır
• Gr_x karakteristik uzunluk x için Grashof sayısıdır
• Pr Prandtl sayısıdır

Yukarıda, akışkan özellikleri Pr, ν, α ve β değerlendirilir, bu sıcaklık şu şekilde tanımlanır:

$${\displaystyle T_{f}={\frac {T_{s}+T_{\infty }}{2}}.}$$

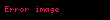
Uniform duvar ısı akısı için, değiştirilmiş Rayleigh sayısı şu şekilde ifade edilir:

$${\displaystyle \mathrm {Ra} _{x}^{*}={\frac {g\beta q''_{o}}{\nu \alpha k}}x^{4}}$$

burada:

• q″_o uniform yüzey ısı akısıdır
• k termal iletkenliktir.

Diğer uygulamalar

Katılaşan alaşımlar

Rayleigh sayısı, katılaşan bir alaşımın peltemsi bölgesinde (İng. mushy) gibi konveksiyonel kararsızlıkları öngörmek için bir kriter olarak da kullanılabilir. Peltemsi bölge Rayleigh sayısı şu şekilde tanımlanır:

$${\displaystyle \mathrm {Ra} ={\frac {{\frac {\Delta \rho }{\rho _{0}}}g{\bar {K}}L}{\alpha \nu }}={\frac {{\frac {\Delta \rho }{\rho _{0}}}g{\bar {K}}}{R\nu }}}$$

burada:

• K ortalama geçirgenliktir (peltemsi bölgenin başlangıç kısmının)
• L karakteristik uzunluk ölçeğidir
• α termal yayınım katsayısıdır
• ν kinematik viskozitedir
• R katılaşma veya izotermal hızdır.

Rayleigh sayısının belirli bir kritik değeri aşması durumunda A-segregatların oluşumu öngörülmektedir. Bu kritik değer, alaşımın bileşiminden bağımsızdır ve bu durum, Rayleigh sayısı kriterinin, Suzuki kriteri gibi konveksiyonel kararsızlıkların öngörüsü için diğer kriterlere göre asıl avantajını oluşturmaktadır.

Torabi Rad ve çalışma arkadaşları, çelik alaşımlar için kritik Rayleigh sayısının 17 olduğunu göstermiştir. Pickering ve çalışma arkadaşları, Torabi Rad'ın kriterini incelemiş ve etkinliğini daha da doğrulamışlardır. Kurşun–kalay ve nikel bazlı süper alaşımlar için de kritik Rayleigh sayıları belirlenmiştir.

Gözenekli ortamlar

Yukarıdaki Rayleigh sayısı, hava veya su gibi kütlesel bir akışkandaki konveksiyon içindir, ancak akışkanın gözenekli bir ortam içinde bulunduğu ve bu ortamı doldurduğu durumlarda da konveksiyon meydana gelebilir; su ile doymuş gözenekli kaya buna örnek gösterilebilir. Bu durumda, Rayleigh sayısı bazen Rayleigh-Darcy sayısı olarak adlandırılır ve buradaki Rayleigh sayısından farklıdır. Gözenekli bir ortamda değil de kütlesel bir akışkanda, göre, ${\displaystyle l}$ büyüklüğündeki bir sıvı bölgesinin düşme hızı ${\displaystyle u\sim \Delta \rho l^{2}g/\eta }$ olur. Gözenekli ortamda, bu ifade ile değiştirilir: ${\displaystyle u\sim \Delta \rho kg/\eta }$, burada ${\displaystyle k}$ gözenekli ortamın geçirgenliğidir. Bu durumda Rayleigh veya Rayleigh-Darcy sayısı şu şekilde ifade edilir:

$${\displaystyle \mathrm {Ra} ={\frac {\rho \beta \Delta Tklg}{\eta \alpha }}}$$

Bu aynı zamanda, katılaşan bir alaşımın peltemsi bölgesindeki için de geçerlidir.

Jeofizik uygulamaları

Jeofizik alanında, Rayleigh sayısı temel bir öneme sahiptir: Bu sayı, Dünya'nın mantosu gibi bir akışkan kütlesi içinde konveksiyonun varlığını ve şiddetini gösterir. Manto, jeolojik zaman ölçeklerinde akışkan gibi davranan bir katı niteliğindedir. Yalnızca içsel ısınma nedeniyle Dünya'nın mantosu için Rayleigh sayısı, Ra_H, şu şekilde ifade edilir:

$${\displaystyle \mathrm {Ra} _{H}={\frac {g\rho _{0}^{2}\beta HD^{5}}{\eta \alpha k}}}$$

burada:

• H birim kütle başına radyojenik ısı üretim oranıdır
• η dinamik viskozitedir
• k termal iletkenliktir
• D manto derinliğidir.

Mantonun çekirdekten ısınması için bir Rayleigh sayısı, Ra_T, şu şekilde tanımlanabilir:

$${\displaystyle \mathrm {Ra} _{T}={\frac {\rho _{0}^{2}g\beta \Delta T_{\text{sa}}D^{3}C_{P}}{\eta k}}}$$

burada:

• ΔT_sa, referans manto sıcaklığı ile çekirdek-manto sınırı arasındaki süperadyabatik sıcaklık farkıdır
• C_P sabit basınçtaki .

Dünya'nın mantosu için yüksek Rayleigh sayısı değerleri, Dünya içinde konveksiyonun güçlü ve zamana bağlı olduğunu, derin iç kısımdan yüzeye taşınan ısının neredeyse tamamının konveksiyonla gerçekleştiğini göstermektedir.

Ayrıca Bakınız

• Grashof sayısı
• Prandtl sayısı
• Reynolds sayısı
• Péclet sayısı
• Nusselt sayısı

Notlar

1. ^ Chandrasekhar, S. (1961). Hydrodynamic and Hydromagnetic Stability. Londra: Oxford University Press. s. 10. ISBN . 
2. ^ ^{a b} Baron Rayleigh (1916). "On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side". London Edinburgh Dublin Phil. Mag. J. Sci. 32 (192). ss. 529-546. doi:10.1080/14786441608635602. 
3. ^ ^{a b c d} Çengel, Yunus; Turner, Robert; Cimbala, John (2017). Fundamentals of thermal-fluid sciences. Fifth. New York, NY. ISBN . OCLC 929985323. 
4. ^ ^{a b c d e} Squires, Todd M.; Quake, Stephen R. (6 Ekim 2005). "Microfluidics: Fluid physics at the nanoliter scale" (PDF). Reviews of Modern Physics. 77 (3). ss. 977-1026. Bibcode:2005RvMP...77..977S. doi:10.1103/RevModPhys.77.977. 
5. ^ ^{a b} Çengel, Yunus A. (2002). Heat and Mass Transfer. Second. McGraw-Hill. s. 466. 
6. ^ Ahlers, Guenter; Grossmann, Siegfried; Lohse, Detlef (22 Nisan 2009). "Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection". Reviews of Modern Physics. 81 (2). ss. 503-537. arXiv:0811.0471 $2. Bibcode:2009RvMP...81..503A. doi:10.1103/RevModPhys.81.503. 
7. ^ M. Favre-Marinet and S. Tardu, Convective Heat Transfer, ISTE, Ltd, London, 2009
8. ^ ^{a b c} Torabi Rad, M.; Kotas, P.; (2013). "Rayleigh number criterion for formation of A-Segregates in steel castings and ingots". Metall. Mater. Trans. A. 44A (9). ss. 4266-4281. Bibcode:2013MMTA...44.4266R. doi:10.1007/s11661-013-1761-4. 
9. ^ Pickering, E.J.; Al-Bermani, S.; Talamantes-Silva, J. (2014). "Application of criterion for A-segregation in steel ingots". Materials Science and Technology. 31 (11). s. 1313. Bibcode:2015MatST..31.1313P. doi:10.1179/1743284714Y.0000000692. 
10. ^ Lister, John R.; Neufeld, Jerome A.; Hewitt, Duncan R. (2014). "High Rayleigh number convection in a three-dimensional porous medium". Journal of Fluid Mechanics (İngilizce). Cilt 748. ss. 879-895. arXiv:0811.0471 $2. Bibcode:2014JFM...748..879H. doi:10.1017/jfm.2014.216. ISSN 1469-7645. 
11. ^ ^{a b} Bunge, Hans-Peter; Richards, Mark A.; Baumgardner, John R. (1997). "A sensitivity study of three-dimensional spherical mantle convection at 10⁸ Rayleigh number: Effects of depth-dependent viscosity, heating mode, and endothermic phase change". . 102 (B6). ss. 11991-12007. Bibcode:1997JGR...10211991B. doi:10.1029/96JB03806 . 

Kaynakça

• Turcotte, D.; Schubert, G. (2002). Geodynamics. 2nd. New York: Cambridge University Press. ISBN . 

Dış bağlantılar

• Rayleigh number calculator