Bu maddede birçok sorun bulunmaktadır. Lütfen sayfayı geliştirin veya bu sorunlar konusunda bir yorum yapın.
|
Savitch Teoremi, uzay karmaşıklığını konu edinen ve bu hususta sonuca varan en eski teoremlerden biridir. Belirlenimsiz makinelerin belirlenimli makinelere dönüştürülmesinde, gerekli olan uzay karmaşıklığını incelemiştir ve beklenenden çok daha küçük uzay gereksinimi olduğunu ortaya koymuştur. Daha formal bir ifadeyle, uzay kullanan bir belirlenimsiz Turing makinesi (nondeterministic turing machine ), belirlenimli bir turing makinesine (deterministic turing machine ) dönüştürülürken uzay gerektirir.
Teorem
Herhangi bir 


İspat fikri
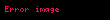


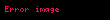


Bunun yerine, çözümü yinelemeli bir algoritma olan, yieldability probleminin yöntemi uygulanmıştır. 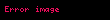



Yieldability problemi
Yinelemeli bir algoritma mantığıyla çözülebilecek olan yieldability probleminin çözümünde aşağıdaki algoritma kullanılır. CANYIELD(


- 1. Eğer
![image]() ise
ise ![image]() olup olmadığına veya
olup olmadığına veya ![image]() 'den
'den ![image]() 'ye tek bir adımda geçip geçmediğine bakılır. Eğer ikisinden biri doğru ise kabul, ikisi de yanlış ise ret döner
'ye tek bir adımda geçip geçmediğine bakılır. Eğer ikisinden biri doğru ise kabul, ikisi de yanlış ise ret döner
- 2. Eğer
![image]() ise bütün
ise bütün ![image]() uzay kullanan ara konfigürasyonlar(
uzay kullanan ara konfigürasyonlar(![image]() ) için:
) için:
- 3. CANYIELD(
![image]() ) çağır
) çağır
- 4. CANYIELD(
![image]() ) çağır
) çağır
- 5. Eğer 3. ve 4. adım kabulse, kabul eder
- 6. Eğer kabul değilse ret döner
İspat

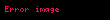







CANYIELD algortimasını kullanır. 


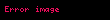


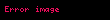


CANYIELD algoritması kabul döner, değilse ret döner.
Şimdi de 



- 1. CANYIELD(
![image]() ,
, ![image]() ,
, ![image]() ) sonucu çıktı olarak döner.
) sonucu çıktı olarak döner.
CANYIELD algoritması kendisini yinelemeli olarak çağırdığında, mevcut durumu; 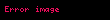









Kaynakça
- ^ Sipser 2006 Introduction to the Theory of Computation, Second
Dış bağlantılar
- Lance Fortnow, Foundations of Complexity, Lesson 18: Savitch's Theorem (18 Mayıs 2009 tarihinde Wayback Machine sitesinde arşivlendi.)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede bircok sorun bulunmaktadir Lutfen sayfayi gelistirin veya bu sorunlar konusunda tartisma sayfasinda bir yorum yapin Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Ocak 2010 Bu maddenin veya maddenin bir bolumunun gelisebilmesi icin matematik konusunda uzman kisilere gereksinim duyulmaktadir Ayrintilar icin lutfen tartisma sayfasini inceleyin veya yeni bir tartisma baslatin Konu hakkinda uzman birini bulmaya yardimci olarak ya da maddeye gerekli bilgileri ekleyerek Vikipedi ye katkida bulunabilirsiniz Ocak 2010 Bu maddede kaynak listesi bulunmasina karsin metin ici kaynaklarin yetersizligi nedeniyle bazi bilgilerin hangi kaynaktan alindigi belirsizdir Lutfen kaynaklari uygun bicimde metin icine yerlestirerek maddenin gelistirilmesine yardimci olun Haziran 2016 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Bu madde tumuyle ya da cogunluguyla tek kaynaga dayaniyor Konuya dair fikir alisverisi tartisma sayfasinda bulunabilir Lutfen baska kaynaklar ekleyerek bu maddeyi gelistirmeye yardim ediniz Haziran 2016 Savitch Teoremi uzay karmasikligini konu edinen ve bu hususta sonuca varan en eski teoremlerden biridir Belirlenimsiz makinelerin belirlenimli makinelere donusturulmesinde gerekli olan uzay karmasikligini incelemistir ve beklenenden cok daha kucuk uzay gereksinimi oldugunu ortaya koymustur Daha formal bir ifadeyle f n displaystyle f n uzay kullanan bir belirlenimsiz Turing makinesi nondeterministic turing machine NTM displaystyle NTM belirlenimli bir turing makinesine deterministic turing machine TM displaystyle TM donusturulurken f n 2 displaystyle f n 2 uzay gerektirir TeoremHerhangi bir f N R displaystyle f N to R fonksiyonu icin f n n displaystyle f n geq n gereksinimi karsilamak kosuluyla NSPACE f n SPACE f n displaystyle NSPACE f n subseteq SPACE f n dir Ispat fikrif n displaystyle f n uzay kullanan bir NTM displaystyle NTM simule ederken akla ilk gelen yol NTM displaystyle NTM nin tum kollarini tek tek hesaplayarak islemi ilerletmektir Bu yolu kullanirken islenen kola ait bilgilerin tutulmasi gerekmektedir f n displaystyle f n uzay kullanan bir kol en kotu ihtimalle 2O f n displaystyle 2 O f n adimda hesaplanabilir Butun kollarin sirayla hesaplanmasi ise hepsinin kayit altinda tutulmasi manasina gelir ki bu 2O f n displaystyle 2 O f n uzay gerektirir Ussel bir iliski kuran bu yontem Savitch teoreminin iddia ettigi uzaydan cok daha fazla uzay gerektirmis olur Bunun yerine cozumu yinelemeli bir algoritma olan yieldability probleminin yontemi uygulanmistir c1 displaystyle c 1 i baslangic c2 displaystyle c 2 yi kabul konfigurasyonu ve t yi NTM displaystyle NTM nin kullanabilecegi maksimum adim sayisi olarak kabul edersek yieldability probleminin cozumu NTM displaystyle NTM nin verilen katari kabul edip etmedigine karar verebilir Yieldability problemiYinelemeli bir algoritma mantigiyla cozulebilecek olan yieldability probleminin cozumunde asagidaki algoritma kullanilir CANYIELD span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c 1 c 2 t semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mn 1 mn mrow msub mo mo msub mi c mi mrow class MJX TeXAtom ORD mn 2 mn mrow msub mo mo mi t mi mstyle mrow annotation encoding application x tex displaystyle c 1 c 2 t annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9jZDRkNjc2ODk2NmM2Y2I0NDMxZmM1ODJmMGEwODAyYWZmMjM1OTY4 svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 671ex width 7 03ex height 2 343ex alt displaystyle c 1 c 2 t noscript img alt image class img layz bg lazy style width 7 03ex height 2 343ex vertical align 0 671ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9jZDRkNjc2ODk2NmM2Y2I0NDMxZmM1ODJmMGEwODAyYWZmMjM1OTY4 svg data alt displaystyle c 1 c 2 t data class mwe math fallback image inline mw invert skin invert span span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c 1 vec 2 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mn 1 mn mrow msub mi v mi mi e mi msub mi c mi mrow class MJX TeXAtom ORD mn 2 mn mrow msub mstyle mrow annotation encoding application x tex displaystyle c 1 vec 2 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8wMDQ4OGNiZTRiMjFlZmRmOWJmZjNiODg2ZTQxMTYxYjIxYjU2OTU4 svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 671ex width 6 333ex height 2 009ex alt displaystyle c 1 vec 2 noscript img alt image class img layz bg lazy style width 6 333ex height 2 009ex vertical align 0 671ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8wMDQ4OGNiZTRiMjFlZmRmOWJmZjNiODg2ZTQxMTYxYjIxYjU2OTU4 svg data alt displaystyle c 1 vec 2 data class mwe math fallback image inline mw invert skin invert span baslangic ve kabul konfigurasyonlari span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle t semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 mi t mi mstyle mrow annotation encoding application x tex displaystyle t annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy82NTY1OGI3YjIyM2FmOWUxYWNjODc3ZDg0ODg4OGVjZGI0NDY2NTYw svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 338ex width 0 84ex height 2 009ex alt displaystyle t noscript img alt image class img layz bg lazy style width 0 84ex height 2 009ex vertical align 0 338ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy82NTY1OGI3YjIyM2FmOWUxYWNjODc3ZDg0ODg4OGVjZGI0NDY2NTYw svg data alt displaystyle t data class mwe math fallback image inline mw invert skin invert span adim sayisi br ul li 1 Eger span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle t 1 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 mi t mi mo mo mn 1 mn mstyle mrow annotation encoding application x tex displaystyle t 1 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy85NzBkZWE0YTVmNWVjNTM1NWM0Y2RkNjJmNjM5NmZiYzhiMWJhYWEx svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 338ex width 5 101ex height 2 176ex alt displaystyle t 1 noscript img alt image class img layz bg lazy style width 5 101ex height 2 176ex vertical align 0 338ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy85NzBkZWE0YTVmNWVjNTM1NWM0Y2RkNjJmNjM5NmZiYzhiMWJhYWEx svg data alt displaystyle t 1 data class mwe math fallback image inline mw invert skin invert span ise span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c 1 c 2 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mn 1 mn mrow msub mo mo msub mi c mi mrow class MJX TeXAtom ORD mn 2 mn mrow msub mstyle mrow annotation encoding application x tex displaystyle c 1 c 2 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9hNGMyNzYwNmYwYzVmMDFjMmYzOTAzNDY3NWUwOGJhYWQ0YzU3Yzc5 svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 671ex width 7 221ex height 2 009ex alt displaystyle c 1 c 2 noscript img alt image class img layz bg lazy style width 7 221ex height 2 009ex vertical align 0 671ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9hNGMyNzYwNmYwYzVmMDFjMmYzOTAzNDY3NWUwOGJhYWQ0YzU3Yzc5 svg data alt displaystyle c 1 c 2 data class mwe math fallback image inline mw invert skin invert span olup olmadigina veya span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c 1 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mn 1 mn mrow msub mstyle mrow annotation encoding application x tex displaystyle c 1 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy83N2I3ZGM2ZDI3OTA5MWQzNTRlMGI5MDg4OWI0NjNiZmE3ZWI3MjQ3 svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 671ex width 2 061ex height 2 009ex alt displaystyle c 1 noscript img alt image class img layz bg lazy style width 2 061ex height 2 009ex vertical align 0 671ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy83N2I3ZGM2ZDI3OTA5MWQzNTRlMGI5MDg4OWI0NjNiZmE3ZWI3MjQ3 svg data alt displaystyle c 1 data class mwe math fallback image inline mw invert skin invert span den span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c 2 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mn 2 mn mrow msub mstyle mrow annotation encoding application x tex displaystyle c 2 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8wYjMwYmExYjI0N2ZiOGQzMzQ1ODBjZWM2ODU2MWU3NDlkMjRhZmYy svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 671ex width 2 061ex height 2 009ex alt displaystyle c 2 noscript img alt image class img layz bg lazy style width 2 061ex height 2 009ex vertical align 0 671ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8wYjMwYmExYjI0N2ZiOGQzMzQ1ODBjZWM2ODU2MWU3NDlkMjRhZmYy svg data alt displaystyle c 2 data class mwe math fallback image inline mw invert skin invert span ye tek bir adimda gecip gecmedigine bakilir Eger ikisinden biri dogru ise kabul ikisi de yanlis ise ret doner br li li 2 Eger span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle t gt 1 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 mi t mi mo gt mo mn 1 mn mstyle mrow annotation encoding application x tex displaystyle t gt 1 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy83MzBmM2RlODU2ZTZmODg1MGY4OWE5Yjk5MGNmYzdmN2JhN2MyOGJm svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 338ex width 5 101ex height 2 176ex alt displaystyle t gt 1 noscript img alt image class img layz bg lazy style width 5 101ex height 2 176ex vertical align 0 338ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy83MzBmM2RlODU2ZTZmODg1MGY4OWE5Yjk5MGNmYzdmN2JhN2MyOGJm svg data alt displaystyle t gt 1 data class mwe math fallback image inline mw invert skin invert span ise butun span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle f n semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 mi f mi mo stretchy false mo mi n mi mo stretchy false mo mstyle mrow annotation encoding application x tex displaystyle f n annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9jMWM0OWZhZDFlY2NjNGU5YWYxZTRmMjNmMzJlZmRjM2FjNGRhOTcz svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 838ex width 4 483ex height 2 843ex alt displaystyle f n noscript img alt image class img layz bg lazy style width 4 483ex height 2 843ex vertical align 0 838ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9jMWM0OWZhZDFlY2NjNGU5YWYxZTRmMjNmMzJlZmRjM2FjNGRhOTcz svg data alt displaystyle f n data class mwe math fallback image inline mw invert skin invert span uzay kullanan ara konfigurasyonlar span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c m semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mi m mi mrow msub mstyle mrow annotation encoding application x tex displaystyle c m annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9lNWE5MmY5ODBhN2NjZjY4MjdiNjkyNWM2ZDY0MjE5ODRkOWM1ODU5 svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 671ex width 2 682ex height 2 009ex alt displaystyle c m noscript img alt image class img layz bg lazy style width 2 682ex height 2 009ex vertical align 0 671ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9lNWE5MmY5ODBhN2NjZjY4MjdiNjkyNWM2ZDY0MjE5ODRkOWM1ODU5 svg data alt displaystyle c m data class mwe math fallback image inline mw invert skin invert span icin br li li 3 CANYIELD span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c 1 c m t 2 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mn 1 mn mrow msub mo mo msub mi c mi mrow class MJX TeXAtom ORD mi m mi mrow msub mo mo mi t mi mrow class MJX TeXAtom ORD mo mo mrow mn 2 mn mstyle mrow annotation encoding application x tex displaystyle c 1 c m t 2 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8zMzk2Mzk0ZDc2OWM2MTgzYjA0Mjk4NWQ5ZDMwMzk1ZjkzZTc1ZTFm svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 838ex width 9 975ex height 2 843ex alt displaystyle c 1 c m t 2 noscript img alt image class img layz bg lazy style width 9 975ex height 2 843ex vertical align 0 838ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8zMzk2Mzk0ZDc2OWM2MTgzYjA0Mjk4NWQ5ZDMwMzk1ZjkzZTc1ZTFm svg data alt displaystyle c 1 c m t 2 data class mwe math fallback image inline mw invert skin invert span cagir br li li 4 CANYIELD span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c m c 2 t 2 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mi m mi mrow msub mo mo msub mi c mi mrow class MJX TeXAtom ORD mn 2 mn mrow msub mo mo mi t mi mrow class MJX TeXAtom ORD mo mo mrow mn 2 mn mstyle mrow annotation encoding application x tex displaystyle c m c 2 t 2 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy80YjAwNWJiMzFiNGVjNDUzMTM1MDViNDNlYmEyOTIwYTgyYzU2MzZm svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 838ex width 9 975ex height 2 843ex alt displaystyle c m c 2 t 2 noscript img alt image class img layz bg lazy style width 9 975ex height 2 843ex vertical align 0 838ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy80YjAwNWJiMzFiNGVjNDUzMTM1MDViNDNlYmEyOTIwYTgyYzU2MzZm svg data alt displaystyle c m c 2 t 2 data class mwe math fallback image inline mw invert skin invert span cagir br li li 5 Eger 3 ve 4 adim kabulse kabul eder br li li 6 Eger kabul degilse ret doner li ul IspatN displaystyle N makinesi f n displaystyle f n uzayda A displaystyle A diline karar veren bir NTM displaystyle NTM olsun A displaystyle A diline karar veren bir belirlenimli TM displaystyle TM M displaystyle M makinesi olusturalim M displaystyle M makinesi N displaystyle N makinesinin herhangi bir konfigurasyonunun belirli adimda cozulup cozulmedigini test etmek icin yukarida bahsedilen CANYIELD algortimasini kullanir w displaystyle w katari N displaystyle N makinesi icin bir girdi katari olsun w displaystyle w katari uzerinde c1 displaystyle c 1 ve c2 displaystyle c 2 konfigurasyonlari icin N displaystyle N makinesi c1 displaystyle c 1 den c2 displaystyle c 2 ye t displaystyle t veya daha az adimda geliyorsa CANYIELD algoritmasi kabul doner degilse ret doner Simdi de N displaystyle N makinesini simule eden bir M displaystyle M makinesi olusturalim span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle M semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 mi M mi mstyle mrow annotation encoding application x tex displaystyle M annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9mODJjYWRlOTg5OGNlZDAyZmRkMDg3MTJlNWYwYzAxNTE3NThhMGRk svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 338ex width 2 442ex height 2 176ex alt displaystyle M noscript img alt image class img layz bg lazy style width 2 442ex height 2 176ex vertical align 0 338ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9mODJjYWRlOTg5OGNlZDAyZmRkMDg3MTJlNWYwYzAxNTE3NThhMGRk svg data alt displaystyle M data class mwe math fallback image inline mw invert skin invert span span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle w semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 mi w mi mstyle mrow annotation encoding application x tex displaystyle w annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy84OGIxZTBjOGUxYmU1ZWJlNjlkMThhODAxMDY3NmZhNDJkNzk2MWU2 svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 338ex width 1 664ex height 1 676ex alt displaystyle w noscript img alt image class img layz bg lazy style width 1 664ex height 1 676ex vertical align 0 338ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy84OGIxZTBjOGUxYmU1ZWJlNjlkMThhODAxMDY3NmZhNDJkNzk2MWU2 svg data alt displaystyle w data class mwe math fallback image inline mw invert skin invert span ul li 1 CANYIELD span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c 1 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mn 1 mn mrow msub mstyle mrow annotation encoding application x tex displaystyle c 1 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy83N2I3ZGM2ZDI3OTA5MWQzNTRlMGI5MDg4OWI0NjNiZmE3ZWI3MjQ3 svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 671ex width 2 061ex height 2 009ex alt displaystyle c 1 noscript img alt image class img layz bg lazy style width 2 061ex height 2 009ex vertical align 0 671ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy83N2I3ZGM2ZDI3OTA5MWQzNTRlMGI5MDg4OWI0NjNiZmE3ZWI3MjQ3 svg data alt displaystyle c 1 data class mwe math fallback image inline mw invert skin invert span span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle c 2 semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msub mi c mi mrow class MJX TeXAtom ORD mn 2 mn mrow msub mstyle mrow annotation encoding application x tex displaystyle c 2 annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8wYjMwYmExYjI0N2ZiOGQzMzQ1ODBjZWM2ODU2MWU3NDlkMjRhZmYy svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 671ex width 2 061ex height 2 009ex alt displaystyle c 2 noscript img alt image class img layz bg lazy style width 2 061ex height 2 009ex vertical align 0 671ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8wYjMwYmExYjI0N2ZiOGQzMzQ1ODBjZWM2ODU2MWU3NDlkMjRhZmYy svg data alt displaystyle c 2 data class mwe math fallback image inline mw invert skin invert span span class mwe math element span class mwe math mathml inline mwe math mathml a11y style display none math xmlns http www w3 org 1998 Math MathML alttext displaystyle 2 f n semantics mrow class MJX TeXAtom ORD mstyle displaystyle true scriptlevel 0 msup mn 2 mn mrow class MJX TeXAtom ORD mi f mi mo stretchy false mo mi n mi mo stretchy false mo mrow msup mstyle mrow annotation encoding application x tex displaystyle 2 f n annotation semantics math span noscript img src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9iZjc1OTIzNzAyNDZiNTk2OTY3MTk0ODcyMTlkNjBmOTU1ZDNhZDc5 svg class mwe math fallback image inline mw invert skin invert aria hidden true style vertical align 0 338ex width 4 564ex height 2 843ex alt displaystyle 2 f n noscript img alt image class img layz bg lazy style width 4 564ex height 2 843ex vertical align 0 338ex data src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9iZjc1OTIzNzAyNDZiNTk2OTY3MTk0ODcyMTlkNjBmOTU1ZDNhZDc5 svg data alt displaystyle 2 f n data class mwe math fallback image inline mw invert skin invert span sonucu cikti olarak doner li ul CANYIELD algoritmasi kendisini yinelemeli olarak cagirdiginda mevcut durumu c1 displaystyle c 1 ve c2 displaystyle c 2 degerlerini tutmak zorunda kalir Oyleyse her bir yineleme adiminda ekstra O f n displaystyle O f n uzay gereklidir Ayrica her bir yineleme adiminda t displaystyle t adim yariya dustugunden toplamda log22f n f n displaystyle log 2 2 f n f n uzay gereklidir O zaman butun simule icin gerekli olan uzay f n f n f n 2 displaystyle f n f n f n 2 olur Bu da Savitch in iddia ettigi gibi O f n 2 displaystyle O f n 2 uzayda bir O f n displaystyle O f n uzay NTM displaystyle NTM bir TM displaystyle TM e donusturulebilir Kaynakca Sipser 2006 Introduction to the Theory of Computation SecondDis baglantilarLance Fortnow Foundations of Complexity Lesson 18 Savitch s Theorem 18 Mayis 2009 tarihinde Wayback Machine sitesinde arsivlendi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans







