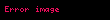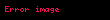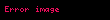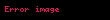- Diğer bilimler için serbestlik derecesi üzerindeki bilgiler için, bakın serbestlik derecesi:
Serbestlik derecesi istatistik'te bir istatistiğin kesin hesaplanmasında kullanılan değerlerin sayısının ne kadar değişme serbestisi olduğunu sayısal olarak verir.
İstatistiksel parametrelerin kestirimleri değişik nicelikte veriye veya bilgiye dayanabilir. Bir parametrenin kestirimi için kullanılması gereken bağımsız bilgi parçalarının sayısına serbestlik derecesi denir. Genellikle, bir kestirim için serbestlik derecesi bu kestirimi elde etmek için kullanılan bağımsız skorlar sayısı eksi bu parametrenin kendisinin kestirimini yapma etaplarında kullanılan parametreler sayısına eşittir.
Matematiksel terimlerle, serbestlik derecesi bir sahasının olur veya vektörün tümünün belirlenmesi için bilinmesi gereken parçaların sayısıdır.
Serbestlik derecesi terimi çok defa olasılık dağılımlarında, ve (yani doğrusal regresyon ve varyans analizi) alanlarında kullanılır. İstatistiğe giriş kitap veya makalelerinde çok kere bu kavram hipotez sınamasında veya olasılık dağılımları parametreleri olarak ilk defa ortaya çıkartılır. Fakat bu kavramin derinden anlaşılabilmesi için kritik olan, kavramın altında bulunan geometrinin kavranmasıdır. Eğer N boyutlu geometri bilinmezse veya modern örnekleme kuramı ikinci elden sadece istatistiğe giriş kitaplarından öğrenilirse, bu kavram pratik anlamı olmayan bir mistik sözcük olmaktan ileri gitmemektedir.
Bu kavram için notasyon ünlü istatistikçi Ronald Fisher tarafından n olarak kullanılmıştır; ama modern istatistik metinlerinde n örneklem büyüklüğü olarak kullanılır. Bu nedenle serbestlik derecesi notasyon olarak (s.d.) veya İngilizceden esinlenerek d.f. ("degree of freedom") olarak ifade edilir.
Artıklar
İstatistiksel modelin veriye uyarlanmasında, hata ve vektörleri genelde vektördeki bileşenlerin sayısından daha kısıtlı bir boyuta sahiptir. Artık veya hata vektörünün bu daha küçük boyuta sahip olma durumuna hatanın "serbestlik derecesi" adı verilir.
Basit bir örnekle açıklanması gerektiğinde:
ifadesindeki x'ler, μ beklenen değerine sahip rassal değişkenler olsun ve
örneklem ortalaması olsun. Öyleyse
büyüklüğü Xi - μ hata tahmininin artıklarını oluşturan bir büyüklüktür.
Hata terimlerinin aksine, artıkların toplamının 0 olması gerekir. Yani n - 1 boyutlu bir uzayda yer alma kısıntı içindedirler. Eğer artıklardan n - 1 tanesi bilinirse, sonuncusu da bulunabilir. Dolayısıyla hata terimi için n - 1 serbestlik derecesi vardır.
modelindeki a ve b'nin yöntemiyle tahmininde
(εi ve dolayısıyla Yi rassaldır). 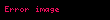
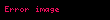
artıkları iki denklemin tanımladığı uzay içinde yer alacak şekilde kısıtlıdırlar:
Dolayısıyla hata terimi için n - 2 serbestlik derecesi vardır.
(Model tanımlanırken büyük y harfi (Y), artıklar tanımlanırken küçük y harfi (y) kullanılmıştır. Birinci ifade teorik rassal değişkenlere bağlıyken ikinci ifade gerçek veriye dayalıdır.)
Olasılık Dağılımlarındaki Parametreler
Hata terimlerinin olasılık dağılımları genelde bu serbestlik dereceleri ile parametrelendirilir. Bu yüzden dağılımından söz edilirken belli bir serbestlik derecesi gerekir, F-dağılımı, t-dağılımı veya bir pay veya paydalarında serbestlik derecesi içerir.
Bu dağılımlarının genel uygulamalarında, serbestlik derecesi yalnızca tam sayı değeri alır. Hâlbuki, konunun temelinde yer alan matematik, çoğu durumda kesirli serbestlik derecesinin alınmasına müsaade eder ki bu da daha karmaşık kullanımlar ortaya çıkarabilir.
Kaynakça
- ^ "Animated Software" tarafından hazırlanan "Glossary of Statistical Terms (İstatistik terimleri sözlüğü)" sitesinde "Degrees of Freedom (serbestlik derecesi)" tanımı 17 Eylül 2018 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişme tarihi=12.08.2008)
- ^ Lane, David M. Degrees of Freedom, Statistics Solutions'in HyperStat Online sitesindeki "Degrees of Freedom (serbestlik derecesi)" maddesi 28 Haziran 2018 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişme tarihi:21.08.2008)
Dış bağlantılar
- İngilizce Wikipedia "Degrees_of_freedom_(statistics)" maddesi 20 Nisan 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişim:20.3.2010)
- Eisenhauer, J.G. (2008) "Degrees of Freedom". Teaching Statistics, Cilt 30(3), say.75–78 (İngilizce) (Erişim:20.3.2010)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Diger bilimler icin serbestlik derecesi uzerindeki bilgiler icin bakin serbestlik derecesi Serbestlik derecesi istatistik te bir istatistigin kesin hesaplanmasinda kullanilan degerlerin sayisinin ne kadar degisme serbestisi oldugunu sayisal olarak verir Istatistiksel parametrelerin kestirimleri degisik nicelikte veriye veya bilgiye dayanabilir Bir parametrenin kestirimi icin kullanilmasi gereken bagimsiz bilgi parcalarinin sayisina serbestlik derecesi denir Genellikle bir kestirim icin serbestlik derecesi bu kestirimi elde etmek icin kullanilan bagimsiz skorlar sayisi eksi bu parametrenin kendisinin kestirimini yapma etaplarinda kullanilan parametreler sayisina esittir Matematiksel terimlerle serbestlik derecesi bir sahasinin olur veya vektorun tumunun belirlenmesi icin bilinmesi gereken parcalarin sayisidir Serbestlik derecesi terimi cok defa olasilik dagilimlarinda ve yani dogrusal regresyon ve varyans analizi alanlarinda kullanilir Istatistige giris kitap veya makalelerinde cok kere bu kavram hipotez sinamasinda veya olasilik dagilimlari parametreleri olarak ilk defa ortaya cikartilir Fakat bu kavramin derinden anlasilabilmesi icin kritik olan kavramin altinda bulunan geometrinin kavranmasidir Eger N boyutlu geometri bilinmezse veya modern ornekleme kurami ikinci elden sadece istatistige giris kitaplarindan ogrenilirse bu kavram pratik anlami olmayan bir mistik sozcuk olmaktan ileri gitmemektedir Bu kavram icin notasyon unlu istatistikci Ronald Fisher tarafindan n olarak kullanilmistir ama modern istatistik metinlerinde n orneklem buyuklugu olarak kullanilir Bu nedenle serbestlik derecesi notasyon olarak s d veya Ingilizceden esinlenerek d f degree of freedom olarak ifade edilir ArtiklarIstatistiksel modelin veriye uyarlanmasinda hata ve vektorleri genelde vektordeki bilesenlerin sayisindan daha kisitli bir boyuta sahiptir Artik veya hata vektorunun bu daha kucuk boyuta sahip olma durumuna hatanin serbestlik derecesi adi verilir Basit bir ornekle aciklanmasi gerektiginde X1 Xn displaystyle X 1 dots X n ifadesindeki x ler m beklenen degerine sahip rassal degiskenler olsun ve X n X1 Xnn displaystyle overline X n X 1 cdots X n over n orneklem ortalamasi olsun Oyleyse Xi X n displaystyle X i overline X n buyuklugu Xi m hata tahmininin artiklarini olusturan bir buyukluktur Hata terimlerinin aksine artiklarin toplaminin 0 olmasi gerekir Yani n 1 boyutlu bir uzayda yer alma kisinti icindedirler Eger artiklardan n 1 tanesi bilinirse sonuncusu da bulunabilir Dolayisiyla hata terimi icin n 1 serbestlik derecesi vardir Yi a bxi ei for i 1 n displaystyle Y i a bx i varepsilon i mathrm for i 1 dots n modelindeki a ve b nin yontemiyle tahmininde ei ve dolayisiyla Yi rassaldir a displaystyle widehat a ve b displaystyle widehat b a ve b tahmin ettigimiz degerler olsun O zaman ei yi a b xi displaystyle e i y i widehat a widehat b x i artiklari iki denklemin tanimladigi uzay icinde yer alacak sekilde kisitlidirlar e1 en 0 displaystyle e 1 cdots e n 0 x1e1 xnen 0 displaystyle x 1 e 1 cdots x n e n 0 Dolayisiyla hata terimi icin n 2 serbestlik derecesi vardir Model tanimlanirken buyuk y harfi Y artiklar tanimlanirken kucuk y harfi y kullanilmistir Birinci ifade teorik rassal degiskenlere bagliyken ikinci ifade gercek veriye dayalidir Olasilik Dagilimlarindaki ParametrelerHata terimlerinin olasilik dagilimlari genelde bu serbestlik dereceleri ile parametrelendirilir Bu yuzden dagilimindan soz edilirken belli bir serbestlik derecesi gerekir F dagilimi t dagilimi veya bir pay veya paydalarinda serbestlik derecesi icerir Bu dagilimlarinin genel uygulamalarinda serbestlik derecesi yalnizca tam sayi degeri alir Halbuki konunun temelinde yer alan matematik cogu durumda kesirli serbestlik derecesinin alinmasina musaade eder ki bu da daha karmasik kullanimlar ortaya cikarabilir Kaynakca Animated Software tarafindan hazirlanan Glossary of Statistical Terms Istatistik terimleri sozlugu sitesinde Degrees of Freedom serbestlik derecesi tanimi 17 Eylul 2018 tarihinde Wayback Machine sitesinde Ingilizce Erisme tarihi 12 08 2008 Lane David M Degrees of Freedom Statistics Solutions in HyperStat Online sitesindeki Degrees of Freedom serbestlik derecesi maddesi 28 Haziran 2018 tarihinde Wayback Machine sitesinde Ingilizce Erisme tarihi 21 08 2008 Dis baglantilarIngilizce Wikipedia Degrees of freedom statistics maddesi 20 Nisan 2010 tarihinde Wayback Machine sitesinde arsivlendi Ingilizce Erisim 20 3 2010 Eisenhauer J G 2008 Degrees of Freedom Teaching Statistics Cilt 30 3 say 75 78 Ingilizce Erisim 20 3 2010
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans