Smith abağı veya Smith diyagramı (Smith chart), radyo ve mikrodalga frekanslarındaki iletim hatlarının tasarımı ve empedans eşlemesinde kullanılan bir grafiktir. Elektrik-elektronik ve haberleşme mühendisleri tarafından kullanılan bu abak Phillip H. Smith (1905–1987) tarafından icat edilmiştir. Smith abağı aynı anda empedans, admitans, yansıma ile saçılma katsayıları (), kazanç konturu ve stabilite gibi çok sayıda parametreyi aynı anda gösterebilmektedir; bu yüksek frekans devreleri dışında mekanik titreşim analizinde de kullanılmasını sağlamıştır. Smith abağı genelde birim yarıçap içinde kullanılır; buna karşın abağın geri kalanı da elektronik osilatör ve stabilite analizinde kullanılmaktadır.

Her ne kadar günümüzde Smith abağı ile empedans eşleme hesaplama problemleri çoğunlukla yazılımlar aracılığıyla çözülse de abak halen RF parametrelerinin bir veya birden fazla frekansta nasıl değiştiğinin gösterilmesinde kullanılmaktadır. Çoğu yüksek frekans devre analizi yazılımı ve empedans ölçme aletleri sonuçları Smith abağı'nda gösterebilmektedir.
Genel bilgiler

Smith abağı iki boyutlu karmaşık yansıma katsayısı düzleminde çizilir. Abak genel olarak empedansa, bazen de admitansa veya ikisine göre göre normalize edilir; bunlar Z, Y ve ZY Smith abakları olarak bilinir. Bu normalizasyon abağın herhangi bir karakteristik ya da sistem empedansına göre kullanılabilmesini sağlar; karakteristik empedans abağın orta noktasına tekabül eder. En genel normalizasyon empedansı 50 ohm'dur. Smith abağından elde edilen sonuç direkt karakterize empedans ya da admitans ile çarpılarak asıl sonuca dönüştürülebilir; aynı zamanda birimsiz değişken olan yansıma katsayıları abaktan direkt okunabilmektedir.
Smith abağı dalga boyu ve açıya göre çevresel bir şekilde ölçeklendirilmiştir. Dalga boyu ölçeği için kullanılır; hat uzunlığı bu devrelerde sinyal jeneratörü ve ilgili yük arasındaki uzaklık olarak alınır. Açı ölçeği ise voltaj yansıma katsayısının açısı için kullanılır. Abak aynı zamanda analizi ve eşlemesinde de kullanılabilir. Smith abağının kullanımı alternatif akım ve iletim hattı teorisine hakim olmayı gerektirmektedir.
Empedans ve admitans her frekansta değiştiğinden, Smith abağı aynı anda sadece tek bir frekans için kullanılabilir; sonuç abaktaki bir nokta olarak gösterilir. Bu genellikle dar bant (bant genişliği %5 ile %10 arası olan) devreler için yeterlidir; daha gen,ş bant aralıkları için banttaki birden fazla frekans abakta analiz edilmelidir. Yakın frekanslarda yapılan frekanslarda elde edilen noktalar birleştirilerek bir gezenek oluşturulabilir.
Smith abağındaki farklı frekans noktalardan oluşan bir gezenek sistemle ilgili farklı detaylar verebilir:
- yükün frekans bandında ne kadar kapasitif veya endüktif olduğu
- farklı frekanslarda empedans eşleme uyumluluğu
- yükün sisteme ne kadar iyi eşlendiği
Çok sayıda noktanın bulunduğu empedans ve admitans grafiklerde Smith abağının doğruluğu azalır; bu bazı durumlarda farklı ölçekleme ile telafi edilebilir.
Matematiksel temelleri

Normalize empedans ve admitans
Karakteristik empedansı 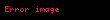

eşleniğiyle bağlıdır. Ohm biriminde bir 
Normalize admitans için benzer bir formül bulunur:
Empedansın SI birimi ohm (Ω) ve admitansın birimi ise siemens'tir (S). Normalize empedans ve admitans ölçüsüzdür. Empedans ve admitansın Smith abağı kullanılmadan önce normalize edilmesi gerekir; abaktan elde edilen sonuç daha sonra karakteristik değerle çarparak asıl sonuca çevrilebilir.
Normalize empedans Smith abağı

İletim hattı teorisine göre bir iletim hattı karakteristik empedanstan (



ve
Bu denklemlerleki ilgili ifadeler:
dalganın zamana bağlı kısmına,
dalganın uzaya bağlı kısmına,
açısal frekansa (rad/s),
frekansa (Hz),
zamana (s),
ile
sabitlere ve
ise yük ile sinyal jeneratörü arasındaki hat mesafesine (m) tekabül eder.
Ayrıca 
Smith abağı bir anda tek bir frekans (

and
Bu denklemde 

Karmaşık yansıma katsayısının hat boyunca değişimi

 uzunluğunda bir kayıpsız hattan yüke bakınca,
uzunluğunda bir kayıpsız hattan yüke bakınca,  arttıkça toplam empedansın değiştiği görülebilir; empedans mavi çizgiyi takip eder. (Bu empedansı yansıma katsayısı
arttıkça toplam empedansın değiştiği görülebilir; empedans mavi çizgiyi takip eder. (Bu empedansı yansıma katsayısı  ile de ifade edebiliriz.) Empedans abağınon ortasındaki mavi daireye bazen SWR dairesi' denir; bu ismini duran dalga oranınından (standing wave ratio) almaktadır.
ile de ifade edebiliriz.) Empedans abağınon ortasındaki mavi daireye bazen SWR dairesi' denir; bu ismini duran dalga oranınından (standing wave ratio) almaktadır.Karmaşık yansıma katsayısı 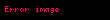
eşitliği tanımlanabilir; C bu denklemde sabit bir sayıdır.



Bu denklemde 

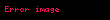
olarak yazılabilir. Bu denklemde 
Bu göz önünde bulundurulacak genel yansıma katsayısı ifadesi,
olarak ifade edilebilir. Bu denklem, bir duran dalgada karmaşık yansıma katsayısı ve empedansın hat üzerinde her yarım dalga boyunda bir tekrar ettiğini gösterir. Karmaşık yansıma katsayısına genelde sadece yansıma katsayısı denir. Abağın dışındaki ölçeği dalga boyuna göre oranlanmıştır ve jeneratörden yüke olan uzaklığı belirtir; sıfırdan 0.50 'a göre oranlanmıştır.
Normalize empedansın hattaki pozisyonuna göre değişimi
Eğer 



and
eşitlikleri ile ifade edilebilir. Bu denklemler bölünür ve voltajların yerine voltaj yansıma katsayısını koyulursa
ve hattın sonundaki normalize empedansı 
empedans formülü elde edilebilir:
.
Alternatif olarak, yansıma katsayısını kullanarak aşağıdaki eşitlik yazılabilir:
Empedans Smith abağı bu denklemler ile ifade edilir. Matematiksel olarak 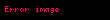

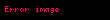

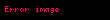
Eşlenmemiş, kayıpsız hattın denklemi,
kayıpsız hattın normalize empedans ile yansıma katsayısı formülü
.
ve Euler formülü kullanılarak,
kayıpsız iletim hattı denklemi türetilebilir.
Burada 


Z Smith abağının bölgeleri
Eğer küresel diyagram bir Kartezyen koordinat sistemi'nin ortasına yerleştirildiyse, genel olarak açılar pozitif x aksına göre saat yönünün tersi bir şekilde ölçülür. Smith abağı da aynı şekilde ölçülmektedir; pozitif x aksı abağın ortasında 

Hattım tamamen eşlenmesi durumunda yansıma katsayısı sıfırlanır; bu abağın ortasındaki "0 yarıçaplı bir daire" ile gösterilir. Hattın bir açık ay da kısa devre ile sonlandırılması durumunda tüm güç yansır ve katsayı birim çember üzerinde bir yerde durur.
Sabit normalize direnç ve reaktans çemberleri
Normalize empedans abağı sabit normalize direnç ve reaktans çemberlerinden oluşur. Abak, karmaşık yansıma düzleminde merkezdeki bir birim çemberinde bulunur; Kartezyen koordinat sisteminde bu daire x aksında (+1,0) ile (−1,0) noktaları ve y aksında (0,+1) ile (0,−1) noktalarından geçer.
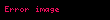

şeklinde yazılabilir; burada a, b, c ve d gerçel sayılardır.
Bunlar normalize empedans ve yansıma sabiti formüllerine yerleştirilirse,
yansıma katsayısı parametrelerin gerçel ve sanal kısımları ile ifade edilebilir:
.
Bu denklem yansıma katsayısının normalize empedansa göre değişimini ifade eder ve abağı oluşturan çemberlerin Kartezyen bir sistemde çiziminde kullanılabilir.
Y Smith abağı

Y Smith abağı Z abağına benzese de bu grafikte normalize admitans kullanılır. Normalize admitans yT, normalize empedans zT'nin çarpımsal tersidir:
Bu göz önünde bulundurularak
ve
eşlenikleri yazılabilir.
Y Smith abağı normalize empedans grafiği ile aynı şekilde gözükse de ölçeği 180° döndürülmüştür; numerik ölçeği aynı kalır. x aksının üstündeki bölge kapasitif, altındaki bölge de endüktif admitansları gösterir. Kapasitif admitansların sanal kısmı pozitif, endüktiflerin ise negatiftir.
Hattın sonunun tamamen eşlenmesi durumunda empedans abağında olduğu gibi yansıma katsayısı sıfırlanır; hattın açık veya kısa devrelenmesi durumunda voltaj yansıma katsayısı birim çemberde bulunur.
Yansıma katsayısı ve normalize empedans örnekleri
Yansıma katsayısının genliği 0.63 ve açısı 60° olan bir nokta kutupsal şekilde 
| Nokta | Yansıma katsayısı (kutupsal) | Normalize empedans (dikey) |
|---|---|---|
| P1 (Endüktif) |  |  |
| P2 (Endüktif) |  |  |
| P3 (Kapasitif) |  |  |
Kaynakça
- ^ Ramo, Whinnery and Van Duzer (1965); "Fields and Waves in Communications Electronics"; John Wiley & Sons; pp 35-39. ISBN
- ^ Smith, P. H.; Transmission Line Calculator; Electronics, Vol. 12, No. 1, pp 29-31, January 1939
- ^ Smith, P. H.; An Improved Transmission Line Calculator; Electronics, Vol. 17, No. 1, p 130, January 1944
- ^ Pozar, David M. (2005); Microwave Engineering, Third Edition (Intl. Ed.); John Wiley & Sons, Inc.; pp 64-71. .
- ^ Gonzalez, Guillermo (1997); Microwave Transistor Amplifiers Analysis and Design, Second Edition; Prentice Hall NJ; pp 93-103. .
- ^ Gonzalez, Guillermo (1997) (op. cit);pp 98-101
- ^ Gonzalez, Guillermo (1997) (op. cit);p 97
- ^ Hayt, William H Jr.; "Engineering Electromagnetics" Fourth Ed; McGraw-Hill International Book Company; pp 428–433. .
- ^ Davidson, C. W.;"Transmission Lines for Communications with CAD Programs";Macmillan; pp 80-85.
Ek kaynaklar
- Mizuhashi, T., Theory of four-terminal impedance transformation circuit and matching circuit, The Journal of the Institute of Electrical Communication Engineers of Japan, pp. 1053–1058, December 1937.
- P.H.Smith 1969 Electronic Applications of the Smith Chart. Kay Electric Company
- G. A. Campbell, "Cisoidal Oscillations", Proc. AIEE, 30, 1-6, pp. 789–824 (1911).
Dış bağlantılar
| Wikimedia Commons'ta Smith abağı ile ilgili ortam dosyaları bulunmaktadır. |
- Mathematical Construction and Properties of the Smith Chart12 Haziran 2020 tarihinde Wayback Machine sitesinde . (İngilizce)
- Smith Chart and Impedance Matching Tutorial with Examples20 Şubat 2020 tarihinde Wayback Machine sitesinde . (İngilizce)
- The Mizuhashi-Smith Chart3 Mart 2013 tarihinde Wayback Machine sitesinde . (İngilizce)
- 3D Smith chart tool2 Mayıs 2020 tarihinde Wayback Machine sitesinde . (Java gerektirir). Aktif ve pasif devre analizi programı
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Smith abagi veya Smith diyagrami Smith chart radyo ve mikrodalga frekanslarindaki iletim hatlarinin tasarimi ve empedans eslemesinde kullanilan bir grafiktir Elektrik elektronik ve haberlesme muhendisleri tarafindan kullanilan bu abak Phillip H Smith 1905 1987 tarafindan icat edilmistir Smith abagi ayni anda empedans admitans yansima ile sacilma katsayilari Snn displaystyle S nn kazanc konturu ve stabilite gibi cok sayida parametreyi ayni anda gosterebilmektedir bu yuksek frekans devreleri disinda mekanik titresim analizinde de kullanilmasini saglamistir Smith abagi genelde birim yaricap icinde kullanilir buna karsin abagin geri kalani da elektronik osilator ve stabilite analizinde kullanilmaktadir Bir empedans Smith abagi Her ne kadar gunumuzde Smith abagi ile empedans esleme hesaplama problemleri cogunlukla yazilimlar araciligiyla cozulse de abak halen RF parametrelerinin bir veya birden fazla frekansta nasil degistiginin gosterilmesinde kullanilmaktadir Cogu yuksek frekans devre analizi yazilimi ve empedans olcme aletleri sonuclari Smith abagi nda gosterebilmektedir Genel bilgilerUzerinde Smith abagi bulunan bir network analizoru HP 8720A Smith abagi iki boyutlu karmasik yansima katsayisi duzleminde cizilir Abak genel olarak empedansa bazen de admitansa veya ikisine gore gore normalize edilir bunlar Z Y ve ZY Smith abaklari olarak bilinir Bu normalizasyon abagin herhangi bir karakteristik ya da sistem empedansina gore kullanilabilmesini saglar karakteristik empedans abagin orta noktasina tekabul eder En genel normalizasyon empedansi 50 ohm dur Smith abagindan elde edilen sonuc direkt karakterize empedans ya da admitans ile carpilarak asil sonuca donusturulebilir ayni zamanda birimsiz degisken olan yansima katsayilari abaktan direkt okunabilmektedir Smith abagi dalga boyu ve aciya gore cevresel bir sekilde olceklendirilmistir Dalga boyu olcegi icin kullanilir hat uzunligi bu devrelerde sinyal jeneratoru ve ilgili yuk arasindaki uzaklik olarak alinir Aci olcegi ise voltaj yansima katsayisinin acisi icin kullanilir Abak ayni zamanda analizi ve eslemesinde de kullanilabilir Smith abaginin kullanimi alternatif akim ve iletim hatti teorisine hakim olmayi gerektirmektedir Empedans ve admitans her frekansta degistiginden Smith abagi ayni anda sadece tek bir frekans icin kullanilabilir sonuc abaktaki bir nokta olarak gosterilir Bu genellikle dar bant bant genisligi 5 ile 10 arasi olan devreler icin yeterlidir daha gen s bant araliklari icin banttaki birden fazla frekans abakta analiz edilmelidir Yakin frekanslarda yapilan frekanslarda elde edilen noktalar birlestirilerek bir gezenek olusturulabilir Smith abagindaki farkli frekans noktalardan olusan bir gezenek sistemle ilgili farkli detaylar verebilir yukun frekans bandinda ne kadar kapasitif veya enduktif oldugu farkli frekanslarda empedans esleme uyumlulugu yukun sisteme ne kadar iyi eslendigi Cok sayida noktanin bulundugu empedans ve admitans grafiklerde Smith abaginin dogrulugu azalir bu bazi durumlarda farkli olcekleme ile telafi edilebilir Matematiksel temelleriBir empedans Smith abagi Bir dalga karakteristik empedansi Z0 olan ve ZL empedansli bir yukle sonlandirilmis bir iletim hattinda ilerliyor Normalize empedansi z ZL Z0 olarak verilir Sinyal G katsayisi ile yansir Abaktaki her bir nokta ayni anda bir z sol alt ve G sag alt degerini gosterir Bu iki deger z 1 G 1 G eslenigiyle ifade edilebilir Normalize empedans ve admitans Karakteristik empedansi Z0 displaystyle Z 0 olan bir iletim hattinin karakteristik admitansi Y0 displaystyle Y 0 ile ifade edilir Bu ikisi Y0 1Z0 displaystyle Y 0 frac 1 Z 0 eslenigiyle baglidir Ohm biriminde bir ZT displaystyle Z text T empedansi karakteristik empedansina bolunerek normalize empedansina zT cevrilebilir zT ZTZ0 displaystyle z text T frac Z text T Z 0 Normalize admitans icin benzer bir formul bulunur yT YTY0 displaystyle y text T frac Y text T Y 0 Empedansin SI birimi ohm W ve admitansin birimi ise siemens tir S Normalize empedans ve admitans olcusuzdur Empedans ve admitansin Smith abagi kullanilmadan once normalize edilmesi gerekir abaktan elde edilen sonuc daha sonra karakteristik degerle carparak asil sonuca cevrilebilir Normalize empedans Smith abagi Acik devre ust ve kisa devre alt ile sonlandirilmis iletim hatlari Bir darbe pulse iki durumda da yansir ama farkli isaretlere sahiptir Siyah noktalar elektronlari ve oklar da elektrik alanlari gosterir Iletim hatti teorisine gore bir iletim hatti karakteristik empedanstan Z0 displaystyle Z 0 farkli bir empedansla ZT displaystyle Z text T sonlandirilirsa bir duran dalga olusur Bu dalga hem ilerleyen VF displaystyle V text F hem de yansiyan VR displaystyle V text R dalgalarin toplamiyla olusur Bu voltajlar kompleks ustel sayilarla ifade edilebilir VF Aexp jwt exp gℓ displaystyle V text F A exp j omega t exp gamma ell ve VR Bexp jwt exp gℓ displaystyle V text R B exp j omega t exp gamma ell Bu denklemlerleki ilgili ifadeler exp jwt displaystyle exp j omega t dalganin zamana bagli kismina exp gℓ displaystyle exp pm gamma ell dalganin uzaya bagli kismina w 2pf displaystyle omega 2 pi f acisal frekansa rad s f displaystyle f frekansa Hz t displaystyle t zamana s A displaystyle A ile B displaystyle B sabitlere ve ℓ displaystyle ell ise yuk ile sinyal jeneratoru arasindaki hat mesafesine m tekabul eder Ayrica g a jb displaystyle gamma alpha j beta iletim katsayisini 1 m ifade etmektedir Bu denklemde a displaystyle alpha kayip katsayisini Np m ve b displaystyle beta ise faz katsayisini rad m gosterir Smith abagi bir anda tek bir frekans w displaystyle omega icin kullanilir bu sekilde dalganin zamana bagli kismi exp jwt displaystyle exp j omega t sabit kalir Tum terimler bu degerle carpilinca ani deger elde edilebilir Bu deger bu frekanstaki tum dalgalar icin ortak oldugundan ihmal edilebilir VF Aexp gℓ displaystyle V text F A exp gamma ell and VR Bexp gℓ displaystyle V text R B exp gamma ell Bu denklemde A displaystyle A ve B displaystyle B yukte sirasiyla ileri ve geri giden voltaj genliklerini gosterir Karmasik yansima katsayisinin hat boyunca degisimi ℓ displaystyle ell uzunlugunda bir kayipsiz hattan yuke bakinca ℓ displaystyle ell arttikca toplam empedansin degistigi gorulebilir empedans mavi cizgiyi takip eder Bu empedansi yansima katsayisi Vreflected Vincident displaystyle V text reflected V text incident ile de ifade edebiliriz Empedans abaginon ortasindaki mavi daireye bazen SWR dairesi denir bu ismini duran dalga oraninindan standing wave ratio almaktadir Karmasik yansima katsayisi G displaystyle Gamma yansiyan dalga ile ileri giden dalganin orani ile hesaplanir Bu goz onunde bulundurularak G VRVF Bexp gℓ Aexp gℓ Cexp 2gℓ displaystyle Gamma frac V text R V text F frac B exp gamma ell A exp gamma ell C exp 2 gamma ell esitligi tanimlanabilir C bu denklemde sabit bir sayidir g displaystyle gamma nin sabit oldugu tek bicimli bir iletim hattinda duran dalganin karmasik yansima katsayisi hattaki pozisyona gore degisir Eger dalga kayipli ise a displaystyle alpha sifirdan farkli ise empedans degisiklikleri bir spiral ile ifade edilir Smith abagi gerektiren cogu problemde kayiplar ihmal edilebilecek kadar kucuktur a 0 displaystyle alpha 0 Buna karsin kayipli durumlarda karmasik yansima katsayisi su hali alir G GLexp 2jbℓ displaystyle Gamma Gamma text L exp 2j beta ell Bu denklemde GL displaystyle Gamma text L yukteki yansima katsayisini ve ℓ displaystyle ell ise yuk ile yansima katsayisi arasindaki hat uzakligini ifade eder Faz katsayisi b displaystyle beta ise b 2pl displaystyle beta frac 2 pi lambda olarak yazilabilir Bu denklemde l displaystyle lambda test frekansinin iletim hatti icindeki dalga boyudur Bu goz onunde bulundurulacak genel yansima katsayisi ifadesi G GLexp 4jplℓ displaystyle Gamma Gamma text L exp left frac 4j pi lambda ell right olarak ifade edilebilir Bu denklem bir duran dalgada karmasik yansima katsayisi ve empedansin hat uzerinde her yarim dalga boyunda bir tekrar ettigini gosterir Karmasik yansima katsayisina genelde sadece yansima katsayisi denir Abagin disindaki olcegi dalga boyuna gore oranlanmistir ve jeneratorden yuke olan uzakligi belirtir sifirdan 0 50 a gore oranlanmistir Normalize empedansin hattaki pozisyonuna gore degisimi Eger V displaystyle V ile I displaystyle I hat boyuncaki voltaj ve hat sonuna giren elektrik akimi olarak tanimlanirsa ilerleyen voltaj VF displaystyle V text F ile yansiyan voltaj VR displaystyle V text R VF VR V displaystyle V text F V text R V and VF VR Z0I displaystyle V text F V text R Z 0 I esitlikleri ile ifade edilebilir Bu denklemler bolunur ve voltajlarin yerine voltaj yansima katsayisini koyulursa G VRVF displaystyle Gamma frac V text R V text F ve hattin sonundaki normalize empedansi zT displaystyle z text T olarak tanimlanirsa zT VZ0I displaystyle z text T frac V Z 0 I empedans formulu elde edilebilir zT 1 G1 G displaystyle z text T frac 1 Gamma 1 Gamma Alternatif olarak yansima katsayisini kullanarak asagidaki esitlik yazilabilir G zT 1zT 1 displaystyle Gamma frac z text T 1 z text T 1 Empedans Smith abagi bu denklemler ile ifade edilir Matematiksel olarak G displaystyle Gamma ve zT displaystyle z text T Mobius donusumleri ile birbirine baglidir G displaystyle Gamma ve zT displaystyle z text T birimleri olmadan karmasik sayilar ile gosterilir Frekansa bagli olarak degistiklerinden hesaplandiklari frekanslar karakteristik empedanslarla birlikte belirtilmelidir G displaystyle Gamma ayrica karmasik duzlemde aci ve genlik olarak ifade edilebilir Yansima katsayisinin genliginin 1 e esit ya da 1 den kucuk olmasi gerekir bundan yola cikarak katsayi cemberin icinde bir nokta olarak ifade edilebilir Smith abaginin olcekleri abagin kutupsal bir grafik olarak kullanilabilmesini saglar Eslenmemis kayipsiz hattin denklemi G Bexp gℓ Aexp gℓ Bexp jbℓ Aexp jbℓ displaystyle Gamma frac B exp gamma ell A exp gamma ell frac B exp j beta ell A exp j beta ell kayipsiz hattin normalize empedans ile yansima katsayisi formulu zT 1 G1 G displaystyle z text T frac 1 Gamma 1 Gamma ve Euler formulu kullanilarak exp j8 cos 8 jsin 8 displaystyle exp j theta cos theta j sin theta kayipsiz iletim hatti denklemi turetilebilir Zin Z0ZL jZ0tan bℓ Z0 jZLtan bℓ displaystyle Z text in Z 0 frac Z text L jZ 0 tan beta ell Z 0 jZ text L tan beta ell Burada Zin displaystyle Z text in ZL displaystyle Z text L ile sonlandirilan ℓ displaystyle ell uzunlugunda kayipsiz bir iletim hattinin girisinde gorulen empedansi ifade eder Bu denklemin eslenigi kayipsiz admitans ile her ikisi icin kayipli durumlarda turetilebilir Z Smith abaginin bolgeleri Eger kuresel diyagram bir Kartezyen koordinat sistemi nin ortasina yerlestirildiyse genel olarak acilar pozitif x aksina gore saat yonunun tersi bir sekilde olculur Smith abagi da ayni sekilde olculmektedir pozitif x aksi abagin ortasinda zT 1 j0 displaystyle z text T 1 pm j0 noktasindan baslayarak zT j displaystyle z text T infty pm j infty noktasina kadar uzamaktadir x aksinin ustundeki bolge enduktif empedanslari pozitif sanal kisim ve altindaki bolge ise kapasitif empedanslari negatif sanal kisim gosterir Hattim tamamen eslenmesi durumunda yansima katsayisi sifirlanir bu abagin ortasindaki 0 yaricapli bir daire ile gosterilir Hattin bir acik ay da kisa devre ile sonlandirilmasi durumunda tum guc yansir ve katsayi birim cember uzerinde bir yerde durur Sabit normalize direnc ve reaktans cemberleri Normalize empedans abagi sabit normalize direnc ve reaktans cemberlerinden olusur Abak karmasik yansima duzleminde merkezdeki bir birim cemberinde bulunur Kartezyen koordinat sisteminde bu daire x aksinda 1 0 ile 1 0 noktalari ve y aksinda 0 1 ile 0 1 noktalarindan gecer G displaystyle Gamma ile z displaystyle z karmasik sayi oldugundan z a jb displaystyle z a jb G c jd displaystyle Gamma c jd seklinde yazilabilir burada a b c ve d gercel sayilardir Bunlar normalize empedans ve yansima sabiti formullerine yerlestirilirse G z 1z 1 displaystyle Gamma frac z 1 z 1 yansima katsayisi parametrelerin gercel ve sanal kisimlari ile ifade edilebilir G c jd a2 b2 1 a 1 2 b2 j 2b a 1 2 b2 displaystyle Gamma c jd left frac a 2 b 2 1 a 1 2 b 2 right j left frac 2b a 1 2 b 2 right Bu denklem yansima katsayisinin normalize empedansa gore degisimini ifade eder ve abagi olusturan cemberlerin Kartezyen bir sistemde ciziminde kullanilabilir Y Smith abagi Kompleks yansima katsayilarinin empedans ve admitans abaklarinda gosterimi Y Smith abagi Z abagina benzese de bu grafikte normalize admitans kullanilir Normalize admitans yT normalize empedans zT nin carpimsal tersidir yT 1zT displaystyle y text T frac 1 z text T Bu goz onunde bulundurularak yT 1 G1 G displaystyle y text T frac 1 Gamma 1 Gamma ve G 1 yT1 yT displaystyle Gamma frac 1 y text T 1 y text T eslenikleri yazilabilir Y Smith abagi normalize empedans grafigi ile ayni sekilde gozukse de olcegi 180 dondurulmustur numerik olcegi ayni kalir x aksinin ustundeki bolge kapasitif altindaki bolge de enduktif admitanslari gosterir Kapasitif admitanslarin sanal kismi pozitif enduktiflerin ise negatiftir Hattin sonunun tamamen eslenmesi durumunda empedans abaginda oldugu gibi yansima katsayisi sifirlanir hattin acik veya kisa devrelenmesi durumunda voltaj yansima katsayisi birim cemberde bulunur Yansima katsayisi ve normalize empedans ornekleri Yansima katsayisinin genligi 0 63 ve acisi 60 olan bir nokta kutupsal sekilde 0 63 60 displaystyle 0 63 angle 60 circ olarak gosterilir bu abaktaki aci olcegini bularak ve birim cemberinin yari capina gore oranlama yaparak cizilebilir Asagidaki tabloda bir empedans Smith abagindaki bazi noktalarin kutupsal yansima katsayilari ve dikey gosterimli normalize empedanslari verilmistir Some examples of points plotted on the normalised impedance Smith chart Nokta Yansima katsayisi kutupsal Normalize empedans dikey P1 Enduktif 0 63 60 displaystyle 0 63 angle 60 circ 0 80 j1 40 displaystyle 0 80 j1 40 P2 Enduktif 0 73 125 displaystyle 0 73 angle 125 circ 0 20 j0 50 displaystyle 0 20 j0 50 P3 Kapasitif 0 44 116 displaystyle 0 44 angle 116 circ 0 50 j0 50 displaystyle 0 50 j0 50 Kaynakca Ramo Whinnery and Van Duzer 1965 Fields and Waves in Communications Electronics John Wiley amp Sons pp 35 39 ISBN Smith P H Transmission Line Calculator Electronics Vol 12 No 1 pp 29 31 January 1939 Smith P H An Improved Transmission Line Calculator Electronics Vol 17 No 1 p 130 January 1944 Pozar David M 2005 Microwave Engineering Third Edition Intl Ed John Wiley amp Sons Inc pp 64 71 0 471 44878 8 Gonzalez Guillermo 1997 Microwave Transistor Amplifiers Analysis and Design Second Edition Prentice Hall NJ pp 93 103 0 13 254335 4 Gonzalez Guillermo 1997 op cit pp 98 101 Gonzalez Guillermo 1997 op cit p 97 Hayt William H Jr Engineering Electromagnetics Fourth Ed McGraw Hill International Book Company pp 428 433 0 07 027395 2 Davidson C W Transmission Lines for Communications with CAD Programs Macmillan pp 80 85 0 333 47398 1Ek kaynaklarMizuhashi T Theory of four terminal impedance transformation circuit and matching circuit The Journal of the Institute of Electrical Communication Engineers of Japan pp 1053 1058 December 1937 P H Smith 1969 Electronic Applications of the Smith Chart Kay Electric Company G A Campbell Cisoidal Oscillations Proc AIEE 30 1 6 pp 789 824 1911 Dis baglantilarWikimedia Commons ta Smith abagi ile ilgili ortam dosyalari bulunmaktadir Mathematical Construction and Properties of the Smith Chart12 Haziran 2020 tarihinde Wayback Machine sitesinde Ingilizce Smith Chart and Impedance Matching Tutorial with Examples20 Subat 2020 tarihinde Wayback Machine sitesinde Ingilizce The Mizuhashi Smith Chart3 Mart 2013 tarihinde Wayback Machine sitesinde Ingilizce 3D Smith chart tool2 Mayis 2020 tarihinde Wayback Machine sitesinde Java gerektirir Aktif ve pasif devre analizi programi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans