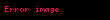Ä°statistik bilim dalÄąnda, Spearman'Äąn sÄąralama korelasyon katsayÄąsÄą veya Spearman'Äąn rho, bu istatistiksel ÃķlçÞyÞ ilk ortaya atan Ä°ngiliz psikolog Charles Edward Spearman'a atfen adlandÄąrÄąlmÄąÅtÄąr. Matematik notasyon olarak çok defa eski Yunan harfi Ï (rho okunur) ile belirtilir. Bir parametrik olmayan istatistik ÃķlçÞsÞdÞr ve iki deÄiÅken arasÄąndaki baÄÄąmlÄąlÄąk, yani korelasyon, ÃķlçÞsÞ olarak bulunup kullanÄąlÄąr. Bu demektir ki Spearman'in rho (Ï) katsayÄąsÄą iki deÄiÅken için hakkÄąnda hiçbir varsayÄąm yapmayarak, bu iki deÄiÅken arasÄąnda bulunan baÄlantÄąnÄąn herhangi bir monotonik fonksiyon ile ne kadar iyi betimlenebilineceÄini deÄerlendirmek amaçlÄą incelemedir.
YÃķntem
Prensip olarak Spearman'Äąn sÄąralama korelasyon katsayÄąsÄą Ï (Pearson çarpÄąm-moment korelasyon katsayÄąsÄąnÄąn) Ãķzel bir halidir. Ï deÄerinin hesaplanmasÄą için iki deÄiÅken (Y ve X) içinde Ãķrneklem verilerinin sÄąralama dÞzeninde olmalarÄą gereklidir. Genel olarak, Ãķrneklem verileri için bu koÅul uygun deÄildir ve veriler sÄąralama dÞzeni halinde olmadan (oransal Ãķlçekli) veya (aralÄąksal Ãķlçekli) veya (sÄąrasal Ãķlçekli) olarak bulunur ve bu halde bir dÃķnÞÅÞmle sÄąralama dÞzeni haline sokulurlar. BÃķylece Ï formÞlÞ için sÄąralama dÞzenli 
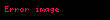
Sonra iki deÄiÅken için karÅÄąlÄąklÄą veri elemanlarÄą (
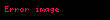
Burada
 : i elamni
ile
sÄąra numaralarÄą arasÄąndaki fark;
- n : iki deÄiÅkenli Ãķrneklemde toplam gÃķzlem sayÄąsÄą.
EÄer sÄąralama esnasÄąnda beraberlikler bulunursa, sÄąralama numaralarÄą verileri olarak kullanÄąlarak klasik (Pearson çarpÄąm-moment korelasyon katsayÄąsÄą) formÞlÞ kullanÄąlmasÄą tavsiye edilir. Bu halde sÄąralama dÞzeni hazÄąrlanÄąrken beraberlikler halinde kullanÄąlacak strateji her beraber sÄąra numaralÄą veriye beraberlik sÄąra ortalama deÄeri verilmesidir (yani 1 2,5 2,5 4 stratejisinin uygulanmasÄądÄąr). Bu halde formÞl Åu olur :
Spearman'in Ï katsayÄąsÄą deÄerleri de (aynÄą Pearson'un çarpÄąm-moment korelasyon katsayÄąsÄą gibi) -1 ile +1 arasÄąnda deÄiÅir. Uç deÄerler (yani Ï=-1 ve Ï=+1 ve yakÄąn deÄerler) iki deÄiÅken sÄąralamasÄą arasÄąnda baÄlantÄąnÄąn çok iyi olduÄunu (eÄer sÄąralamalar noktalar olarak bir konulursa hepsinin çizilen bir doÄru Þzerinde olduÄunu) gÃķsterirler. EÄer Ï<0 ise, sÄąralamalar arasÄąnda indirek aksi deÄiÅme vardÄąr; yani biri artÄąnca diÄeri azalÄąr ve aksi olur. EÄer Ï>0 ise sÄąralamalar arasÄąnda birlikte (yani birlikte artma veya eksilme) deÄiÅme gÃķrÞlÞr. EÄer Ï=0 ise, sÄąralamalar arasÄąnda hiçbir baÄlantÄąnÄą bulunmadÄąÄÄą (ve serpme diyagrami Þzerinde noktalarÄąn rastgele daÄÄąldÄąklarÄą) sonucu Ã§ÄąkartÄąlÄąr.
DiÄer sÄąralama korelasyon ÃķlçÞleriyle iliÅki
Spearman'in Ï sÄąralama korelasyon katsayÄąsÄą ile Ï, bu ÃķlçÞleri destekleyen varsayÄąmlara gÃķre, birbiri ile aynÄądÄąr. Ancak aynÄą Ãķrneklem veriler serisi ile hesaplanan Spearman Ï katsayÄąsÄą deÄeri ile Kendal'Äąn Ï katsayÄąsÄą deÄeri birbirinden farklÄą olacaktÄąr. Buna baÅlÄąca neden hesaplama formÞllerin geliÅtirilmesi için kullanÄąlan mantÄąksal Ãķnerimlerin baÅka olmasÄą ve bu nedenle bibirinden çok deÄiÅik iki formÞlÞn ortaya Ã§ÄąkmasÄądÄąr. Bu iki katsayÄą arasÄąndaki iliÅki bir eÅitsizlik ile ifade edilmiÅtir:
- -1 < = 3 * Ï - 2 * Ï < = 1
Spearman'in Ï katsayÄąsÄą sÄąralama dÞzeni verileri ile Pearson çarpÄąm-moment korelasyon katsayÄąsÄąnÄąn hesaplanmasÄądÄąr ve temel mantik olarak bu iki katsayÄą aynÄą Ãķnerimlere dayanÄąrlar. Halbuki Kendal'in Ï katsayÄąsÄą bir olasÄąlÄąk ifade eder ve uyuÅma ve uyuÅmama puanlarÄą için gerçek toplam ile maksimum mÞmkÞn toplam arasÄąnda bir orantÄądÄąr.
ÃrneÄin
Tabloda iki deÄiÅken X ve Y için n=8 gÃķzlem sayÄąlÄą Ãķrneklem verileri için Spearman'Äąn sÄąralama korelasyon katsayÄąsÄą Ï hesaplanmasÄą için ÃķrneÄin verilmektedir. [A] ve [B] sÞtunlarÄąnda bu iki deÄiÅken X ve Y için Ãķrneklem verileri verilmiÅtir. [C] ve [D] sÞtunlarÄąnda bu iki deÄiÅkenlerin verileri için ayrÄą ayrÄą sÄąralama dÞzeni uygulanÄąp sÄąra numaralarÄą x ve y olarak verilmiÅtir. X için verilerde 2 deÄiÅik beraberlik gÃķrÞlmektedir: 3 ve 10. Bu nedenle iki tekrarlÄą 3 için verilen sÄąra numaralarÄą ortalamasÄą (2+3)/2= 2,5 dur. AynÄą Åeklide 2 tekrarlÄą 10 için sÄąra numaralarÄą 7,5 7,5 olarak verilmiÅtir. Y için verilerde ise 1,5 için 2 beraberlik ve 5 için 2 beraberlik bulunmaktadÄąr ve bunlara da ortalama sÄąra numaralarÄą verilmiÅtir. SÞtun [E]de sÄąra numaralarÄą farklarÄą d verilmekte ve son [F] sÞtununda fark kareleri d2 hesaplanmaktadÄąr.
| [A] | [B] | [C] | [D] | [E] | [F] |
| X | Y | x : X için sÄąralama | y : Y için sÄąralama | d : SÄąralama farklarÄą | d2 : FarklarÄąn karesi |
| 2 | 1,5 | 1 | 2,5 | -1,5 | 2,25 |
| 3 | 1,5 | 2,5 | 2,5 | 0 | 0 |
| 3 | 4 | 2,5 | 5 | -2,5 | 6,25 |
| 5 | 3 | 4 | 4 | 0 | 0 |
| 5,5 | 1 | 5 | 1 | 4 | 16 |
| 8 | 5 | 6 | 6,5 | -0,5 | 0,25 |
| 10 | 5 | 7,5 | 6,5 | 1 | 1 |
| 10 | 9,5 | 7,5 | 8 | -0,5 | 0,25 |
| Â | Â | Â | Â | Kareler ToplamÄą | 26 |
Fark kareleri toplamÄą 
ve Åu sonuç bulunur 
Bu Ï=0.6 deÄeri sÄąfÄąra yakÄąn pozitiftir. SÄąfÄąra yakÄąnlÄąÄÄą X ve Y sÄąralamalarÄą arasÄąndaki baÄlantÄąnÄąn (korelasyonun) az olduÄunu gÃķsterir ve negatif olma ise var zayÄąf baÄlantÄąnÄąn aksi yÃķnde olduÄunu ifade eder (yani X sÄąralamasÄą artarsa Y sÄąralamasÄą dÞÅer ve aksi olur).
Bu veriler içinde beraberlikler bulunmaktadÄąr. Bu nedenle kullanÄąlan genel Ï formÞlÞ uygun sonuç vermeyebilir. Daha uygun sonuç bulmak için x ve y sÄąra numaralarÄą için Pearson'un çarpÄąm-moment korelasyon katsayÄąsÄą bulunmasÄą tavsiye edilmektedir.
Ï kestirimi için anlamlÄąlÄąk sÄąnamasÄą
EÄer hesaplar ve anlamlÄąlÄąk sÄąnamasÄą el hesap makineleri ile yapÄąlmakta ise, klasik Ã§ÄąkarÄąmsal istatistik yÃķntemleri kullanÄąlmalÄądÄąr.
Ï kestirminin anlamlÄąlÄąk sÄąnanmasÄą için en basit yaklaÅÄąm belirli gÃķzlem sayÄąsÄą ve belirli anlamlÄąlÄąk dÞzeyi deÄerleri için hazÄąrlanmÄąÅ Ãķzel tablolar kullanÄąlarak baÅarÄąlÄąr. Ancak bu tablolar belirli veri sayÄąsÄą ve anlamlÄąlÄąk dÞzeyi dÄąÅÄąnda ise kullanÄąlamaz.
Ãnemli kompÞter istatistik paketleri Spearman'in sÄąralamalÄą korelasyon katsayÄąsÄąnÄą hesapladÄąklarÄą zaman ek olarak anlamlÄąlÄąk sÄąnamasÄą için p-deÄerini de yanÄąnda vermektedirler.
DiÄer bir alternatif yaklaÅÄąm eÄer Ãķrneklem hacmi 20'den bÞyÞk ise uygulanabilir. Bu halde Student'in t daÄÄąlÄąmÄąna bir yaklaÅÄąm kullanÄąlÄąr:
deÄiÅkeni sÄąfÄąr hipotez olan Ï=0 için bir Student'in t daÄÄąlÄąmÄą gÃķsterir. Ancak biraz zayÄąftÄąr ve sifir hipotez ret edilnece Ï'nun ne deÄer alacaÄÄąnÄą gÃķstermez.
GÃķzÞmlenen Ï deÄerinin anlamlÄą Åekilde 0dan baÅka deÄerde olmasÄąnÄą sÄąnama için modern yaklaÅÄąm olarak yÃķntemi kullanÄąlmaktadÄąr ve bu tip sÄąnama için, sÄąfÄąr hipotez verilmiÅse anakÞtle Ï deÄerinin Ãķrneklemle elde edilen deÄerde ve ondan bÞyÞk olma olasÄąlÄąÄÄą hesap edilir. Bu modern sÄąnama yÃķntemi ancak kompÞter programÄą yazabilen ve kompÞteri iyi kullanabilen bir bilim insanÄą için çok kolay olabilir.
AyrÄąca bakÄąnÄąz
- SÄąralama korelasyonu
- ,
- (Pearson çarpÄąm-moment korelasyon katsayÄąsÄą)
- Korelasyon
Kaynakça
- ^ Spearman,C.(1904) "The proof and measurement of association between two things" Amer.J.Psychol. C.15 say.72â101
- ^ Kendall,M.G. (1962) Rank correlation methods, Griffin
- ^ Hollander,M. ve Wolfe,D.A. (1973) Nonparametric statistical methods, New York:Wiley
- ^ a b Myers,J.L. ve Well,A.D. (2003), Research Design and Statistical Analysis (2.ed.), Lawrence Erlbaum
- ^ a b Siegel,S. ve Castellan,N.J. (1988), Nonparametric statistics for the behavioral sciences 2. ed. New York: McGraw-Hill
DÄąÅ baÄlantÄąlar
- [1]14 Nisan 2012 tarihinde Wayback Machine sitesinde . KÞçÞk Ãķrneklemler için Ï için kritik deÄerler tablosu.
- [2] 17 MayÄąs 2008 tarihinde Wayback Machine sitesinde . Online Ï hesaplayÄącÄąsÄą.
- Beraberlikler olursa kullanÄąlabilecek bir diÄer formÞl vermekte.
- [4]30 Mart 2012 tarihinde Wayback Machine sitesinde . Spearman'Äąn sÄąralama korelasyon katsayÄąsÄą: ÃÄrenciler için hazÄąrlanmÄąÅ bir Ãķrnek problem çÃķzÞmÞ ve notlar. Hesaplama için Microsoft Excel kullanÄąlmasÄą da gÃķsterilir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kÞtÞphane, kÞtÞbhane, ara, ara bul, bul, herÅey, ne arasanÄąz burada,hikayeler, makale, kitaplar, ÃķÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tÞrk, tÞrkçe, turkce, nasÄąl yapÄąlÄąr, ne demek, nasÄąl, yapmak, yapÄąlÄąr, indir, Þcretsiz, Þcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mÞzik, ÅarkÄą, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Istatistik bilim dalinda Spearman in siralama korelasyon katsayisi veya Spearman in rho bu istatistiksel olcuyu ilk ortaya atan Ingiliz psikolog Charles Edward Spearman a atfen adlandirilmistir Matematik notasyon olarak cok defa eski Yunan harfi r rho okunur ile belirtilir Bir parametrik olmayan istatistik olcusudur ve iki degisken arasindaki bagimlilik yani korelasyon olcusu olarak bulunup kullanilir Bu demektir ki Spearman in rho r katsayisi iki degisken icin hakkinda hicbir varsayim yapmayarak bu iki degisken arasinda bulunan baglantinin herhangi bir monotonik fonksiyon ile ne kadar iyi betimlenebilinecegini degerlendirmek amacli incelemedir YontemPrensip olarak Spearman in siralama korelasyon katsayisi r Pearson carpim moment korelasyon katsayisinin ozel bir halidir r degerinin hesaplanmasi icin iki degisken Y ve X icinde orneklem verilerinin siralama duzeninde olmalari gereklidir Genel olarak orneklem verileri icin bu kosul uygun degildir ve veriler siralama duzeni halinde olmadan oransal olcekli veya araliksal olcekli veya sirasal olcekli olarak bulunur ve bu halde bir donusumle siralama duzeni haline sokulurlar Boylece r formulu icin siralama duzenli xi displaystyle x i ve yi displaystyle y i orneklem verileri kullanilir Sonra iki degisken icin karsilikli veri elemanlari xi displaystyle x i ve yi displaystyle y i nin sira numaralari arasindaki fark di displaystyle d i i 1 n olarak bulunur Bu tum karsilikli veriler i 1 n icin uygulanir Eger sira numaralari arasinda hic beraberlik yoksa r degerini bulmak icin su formul kullanilir r 1 6 di2n n2 1 displaystyle rho 1 frac 6 sum d i 2 n n 2 1 Burada di xi yi displaystyle d i x i y i i elamni Xi displaystyle X i ile Yi displaystyle Y i sira numaralari arasindaki fark n iki degiskenli orneklemde toplam gozlem sayisi Eger siralama esnasinda beraberlikler bulunursa siralama numaralari verileri olarak kullanilarak klasik Pearson carpim moment korelasyon katsayisi formulu kullanilmasi tavsiye edilir Bu halde siralama duzeni hazirlanirken beraberlikler halinde kullanilacak strateji her beraber sira numarali veriye beraberlik sira ortalama degeri verilmesidir yani 1 2 5 2 5 4 stratejisinin uygulanmasidir Bu halde formul su olur r n xiyi xi yi n xi2 xi 2 n yi2 yi 2 displaystyle rho frac n sum x i y i sum x i sum y i sqrt n sum x i 2 sum x i 2 sqrt n sum y i 2 sum y i 2 Spearman in r katsayisi degerleri de ayni Pearson un carpim moment korelasyon katsayisi gibi 1 ile 1 arasinda degisir Uc degerler yani r 1 ve r 1 ve yakin degerler iki degisken siralamasi arasinda baglantinin cok iyi oldugunu eger siralamalar noktalar olarak bir konulursa hepsinin cizilen bir dogru uzerinde oldugunu gosterirler Eger r lt 0 ise siralamalar arasinda indirek aksi degisme vardir yani biri artinca digeri azalir ve aksi olur Eger r gt 0 ise siralamalar arasinda birlikte yani birlikte artma veya eksilme degisme gorulur Eger r 0 ise siralamalar arasinda hicbir baglantini bulunmadigi ve serpme diyagrami uzerinde noktalarin rastgele dagildiklari sonucu cikartilir Diger siralama korelasyon olculeriyle iliskiSpearman in r siralama korelasyon katsayisi ile t bu olculeri destekleyen varsayimlara gore birbiri ile aynidir Ancak ayni orneklem veriler serisi ile hesaplanan Spearman r katsayisi degeri ile Kendal in t katsayisi degeri birbirinden farkli olacaktir Buna baslica neden hesaplama formullerin gelistirilmesi icin kullanilan mantiksal onerimlerin baska olmasi ve bu nedenle bibirinden cok degisik iki formulun ortaya cikmasidir Bu iki katsayi arasindaki iliski bir esitsizlik ile ifade edilmistir 1 lt 3 t 2 r lt 1 Spearman in r katsayisi siralama duzeni verileri ile Pearson carpim moment korelasyon katsayisinin hesaplanmasidir ve temel mantik olarak bu iki katsayi ayni onerimlere dayanirlar Halbuki Kendal in t katsayisi bir olasilik ifade eder ve uyusma ve uyusmama puanlari icin gercek toplam ile maksimum mumkun toplam arasinda bir orantidir OrneginTabloda iki degisken X ve Y icin n 8 gozlem sayili orneklem verileri icin Spearman in siralama korelasyon katsayisi r hesaplanmasi icin ornegin verilmektedir A ve B sutunlarinda bu iki degisken X ve Y icin orneklem verileri verilmistir C ve D sutunlarinda bu iki degiskenlerin verileri icin ayri ayri siralama duzeni uygulanip sira numaralari x ve y olarak verilmistir X icin verilerde 2 degisik beraberlik gorulmektedir 3 ve 10 Bu nedenle iki tekrarli 3 icin verilen sira numaralari ortalamasi 2 3 2 2 5 dur Ayni seklide 2 tekrarli 10 icin sira numaralari 7 5 7 5 olarak verilmistir Y icin verilerde ise 1 5 icin 2 beraberlik ve 5 icin 2 beraberlik bulunmaktadir ve bunlara da ortalama sira numaralari verilmistir Sutun E de sira numaralari farklari d verilmekte ve son F sutununda fark kareleri d2 hesaplanmaktadir A B C D E F X Y x X icin siralama y Y icin siralama d Siralama farklari d2 Farklarin karesi2 1 5 1 2 5 1 5 2 253 1 5 2 5 2 5 0 03 4 2 5 5 2 5 6 255 3 4 4 0 05 5 1 5 1 4 168 5 6 6 5 0 5 0 2510 5 7 5 6 5 1 110 9 5 7 5 8 0 5 0 25 Kareler Toplami 26 Fark kareleri toplami di2 26 displaystyle sum d i 2 26 olarak bulunmustur Hesaplarin degerleri formule soyle konulur r 1 6 268 82 1 displaystyle rho 1 frac 6 times 26 8 8 2 1 ve su sonuc bulunur r 0 6 displaystyle rho 0 6 Bu r 0 6 degeri sifira yakin pozitiftir Sifira yakinligi X ve Y siralamalari arasindaki baglantinin korelasyonun az oldugunu gosterir ve negatif olma ise var zayif baglantinin aksi yonde oldugunu ifade eder yani X siralamasi artarsa Y siralamasi duser ve aksi olur Bu veriler icinde beraberlikler bulunmaktadir Bu nedenle kullanilan genel r formulu uygun sonuc vermeyebilir Daha uygun sonuc bulmak icin x ve y sira numaralari icin Pearson un carpim moment korelasyon katsayisi bulunmasi tavsiye edilmektedir r kestirimi icin anlamlilik sinamasiEger hesaplar ve anlamlilik sinamasi el hesap makineleri ile yapilmakta ise klasik cikarimsal istatistik yontemleri kullanilmalidir r kestirminin anlamlilik sinanmasi icin en basit yaklasim belirli gozlem sayisi ve belirli anlamlilik duzeyi degerleri icin hazirlanmis ozel tablolar kullanilarak basarilir Ancak bu tablolar belirli veri sayisi ve anlamlilik duzeyi disinda ise kullanilamaz Onemli komputer istatistik paketleri Spearman in siralamali korelasyon katsayisini hesapladiklari zaman ek olarak anlamlilik sinamasi icin p degerini de yaninda vermektedirler Diger bir alternatif yaklasim eger orneklem hacmi 20 den buyuk ise uygulanabilir Bu halde Student in t dagilimina bir yaklasim kullanilir t r 1 r2 n 2 displaystyle t frac rho sqrt 1 rho 2 n 2 r tn 2 t2 displaystyle rho frac t sqrt n 2 t 2 degiskeni sifir hipotez olan r 0 icin bir Student in t dagilimi gosterir Ancak biraz zayiftir ve sifir hipotez ret edilnece r nun ne deger alacagini gostermez Gozumlenen r degerinin anlamli sekilde 0dan baska degerde olmasini sinama icin modern yaklasim olarak yontemi kullanilmaktadir ve bu tip sinama icin sifir hipotez verilmisse anakutle r degerinin orneklemle elde edilen degerde ve ondan buyuk olma olasiligi hesap edilir Bu modern sinama yontemi ancak komputer programi yazabilen ve komputeri iyi kullanabilen bir bilim insani icin cok kolay olabilir Ayrica bakinizSiralama korelasyonu Pearson carpim moment korelasyon katsayisi KorelasyonKaynakca Spearman C 1904 The proof and measurement of association between two things Amer J Psychol C 15 say 72 101 Kendall M G 1962 Rank correlation methods Griffin Hollander M ve Wolfe D A 1973 Nonparametric statistical methods New York Wiley a b Myers J L ve Well A D 2003 Research Design and Statistical Analysis 2 ed Lawrence Erlbaum a b Siegel S ve Castellan N J 1988 Nonparametric statistics for the behavioral sciences 2 ed New York McGraw HillDis baglantilar 1 14 Nisan 2012 tarihinde Wayback Machine sitesinde Kucuk orneklemler icin r icin kritik degerler tablosu 2 17 Mayis 2008 tarihinde Wayback Machine sitesinde Online r hesaplayicisi Beraberlikler olursa kullanilabilecek bir diger formul vermekte 4 30 Mart 2012 tarihinde Wayback Machine sitesinde Spearman in siralama korelasyon katsayisi Ogrenciler icin hazirlanmis bir ornek problem cozumu ve notlar Hesaplama icin Microsoft Excel kullanilmasi da gosterilir
 AzÉrbaycanca
AzÉrbaycanca ÐÐĩÐŧаŅŅŅКŅ
ÐÐĩÐŧаŅŅŅКŅ Dansk
Dansk Deutsch
Deutsch EspaÃąola
EspaÃąola Français
Français Indonesia
Indonesia Italiana
Italiana æĨæŽčŠ
æĨæŽčŠ ŌазаŌ
ŌазаŌ Lietuvos
Lietuvos Nederlands
Nederlands PortuguÊs
PortuguÊs Ð ŅŅŅКÐļÐđ
Ð ŅŅŅКÐļÐđ ā·ā·āķā·āķ―
ā·ā·āķā·āķ― āđāļāļāđāļāļĒ
āđāļāļāđāļāļĒ TÞrkçe
TÞrkçe ÐĢКŅаŅÐ―ŅŅКа
ÐĢКŅаŅÐ―ŅŅКа äļåäšš
äļåäšš United State
United State Afrikaans
Afrikaans