Stokastik diferansiyel denklemler

Matematikte bir stokastik diferansiyel denklem, içinde bir ya da birden fazla terimin stokastik süreç olduğu ve çözümün de, eğer varsa, yine stokastik süreç olduğu bir diferansiyel denkleme verilen addır. Başka bir deyişle, bir stokastik diferansiyel denklem adi diferansiyel denklem teriminin stokastik süreçlere genelleştirilmesidir.

Stokastik diferansiyel denklemlerin soyut matematikte bir çok kullanım sahası vardır. Örneğin, en basitinden, deterministik faktörleri içinde barındırmakla kalmayıp, gürültü gibi, stokastik etkileri de içeren zamana bağlı süreçleri modellemek için kullanılır. En bilinen uygulama alanları arasında, hareketlerinin modellenmesi, ve maruz kalmış fizik sistemleri gibi stokastik modeller de vardır.

Stokastik diferansiyel denklemlerde rassal diferansiyeller mevcuttur ve bu diferensiyeller en basitinden bir Brown hareketinin ya da daha genel haliyle bir diferansiyeli olarak hesap edilen beyaz gürültü gibi olabilir. Yine de, gibi sıçrama süreçleri veya sıçramalı yarı martingaller gibi başka tür rassal hareketlerin de stokastik diferansiyel denklemlerle modellenmesi ve temsili mümkündür. Stokastik diferansiyel denklemlerin türevlenebilir manifoldlara genelleştirilmesi de mümkündür.

Tarihçe

Stokastik diferansiyel denklemler, 1905'te Albert Einstein ve Marian Smoluchowski'nin çalışmalarıyla Brown hareketi teorisinde ortaya çıkmıştır; ancak, 1900'de Brown hareketinin modellenmesiyle tanınan ilk kişi olmuş ve günümüzde olarak bilinen stokastik diferansiyel denklemin çok erken bir örneğini vermiştir. Bu erken örneklerden bazıları, Fransız fizikçi Langevin'in adıyla olarak da adlandırılan doğrusal stokastik diferansiyel denklemlerdi ve rassal bir kuvvete maruz kalan harmonik osilatörün hareketini tanımlıyordu.

Stokastik diferansiyel denklemlerin matematiksel teorisi, kavramını ortaya atan ve doğrusal olmayan stokastik diferansiyel denklemlerin çalışmasını başlatan Japon matematikçi Kiyosi Itô'nun çığır açan çalışmalarıyla 1940'larda geliştirilmiştir. Ito'nın çalışmalarından sonra stokastik integral ile birlikte stokastik diferansiyel denklemler de anlam kazandı ve stokastik hesap ya da stokastik analiz verilen bir alanın ana hatları ortaya çıkmaya başladı. Daha sonra Rus fizikçi Stratonoviç tarafından başka bir yaklaşım önerilmiş ve sıradan kalkülüse benzer bir stokastik hesabın önünü açılmıştır.

Terminoloji

Literatürde stokastik diferansiyel denklemlerin en yaygın biçimi, sağ taraftaki terimlerin beyaz gürültü değişkenine bağlı başka bir terim tarafından bozulması ya da tedirgemesiyle (pertürbasyon) oluşan adi diferansiyel denklemdir. Çoğu zaman, stokastik diferansiyel denklemler, stokastik fark denklemlerine karşılık gelen sürekli zaman limiti olarak da anlaşılır; ancak, stokastik diferansiyel denklemlerin bu şekilde anlaşılması aslında belirsizlik içermektedir ve genelde bu açıdan verilen tanımı tamamlayabilecek bir integralin tanımının verilmesini de zorunlu kılmaktadır.

Böyle bir matematiksel tanım ilk olarak 1940'larda tarafından önerilmiş ve bugün olarak bilinen alan açılmıştır. Daha sonra, Rus fizikçi Stratonoviç tarafından başka bir yapı önerilmiş ve ortaya çıkmıştır. Itô integrali ve Stratonoviç integrali birbiriyle ilişkili ancak farklı kavramlardır. Bu ikisinin arasındaki seçim ise elde var olan probleme ya da dikkate alınan uygulamaya bağlıdır. Itô hesabı, değişkenin zaman olduğu uygulamalarda doğal olan öngörülemezlik veya nedensellik kavramına dayanmaktadır. Öte yandan Stratonoviç hesabı, kalkülüse benzeyen kurallara sahiptir ve manifoldlar üzerindeki rassal hareket gibi geometrik problemlerle uğraşırken onu daha doğal hale getiren içsel geometrik özelliklere sahiptir. Ancak, manifoldlar üzerindeki rastgele hareketi Itô tipli stokastik diferansiyel denklemler aracılığıyla modellemek mümkündür ve hatta bazı durumlarda (örneğin, altmanifoldlar üzerindeki stokastik diferansiyel denklemleri en iyi şekilde yaklaşıklamaya çalışırken) tercih edilir.

Stokastik diferansiyel denklemlere yönelik alternatif bir görüş ise difeomorfizmaların stokastik akışıdır. Bu anlayış belirsiz değildir ve stokastik fark denklemlerinin sürekli zaman limitinin Stratonoviç versiyonuna karşılık gelir. Stokastik diferansiyel denklemlerle ilişkili olan bu tür denklemlere örnekler veya olasılık yoğunluk fonksiyonlarının zaman evrimini tanımlayan Fokker-Planck denklemi. Fokker-Planck evriminin diferansiyel formların zamansal evrimine yönelik genelleştirilmesi kavramı üzerinden sağlanır.

Fiziki bilimlerde, "" teriminin kullanımında bir belirsizlik vardır. Langevin denklemleri daha genel bir biçimde olabilirken, bu terim, tipik olarak gradyan akış vektör alanlarına sahip dar bir stokastik diferansiyel denklemler sınıfını ifade eder. Bu sınıf çok popülerdir çünkü Parisi–Sourlas stokastik nicemleme prosedürünün bir başlangıç noktasıdır ve yakından ilişkili bir ${\displaystyle N=2}$ süpersimetrik modelin yolunu açar. Ancak fiziksel bakış açısıyla, bu stokastik diferansiyel denklemler sınıfı çok ilginç değildir; çünkü, asla topolojik süpersimetrinin kendiliğinden bozulmasını göstermez. Yâni, (aşırı sönümlenmiş) Langevin denklemleri asla kaotik değildir.

Stokastik kalkülüs

Brown hareketi veya ilk başta matematiksel olarak son derece karmaşık bulunmuştur. hemen hemen kesinlikle hiçbir yerde türevlenebilir değildir; bu nedenle, kendi kalkülüs kurallarını gerektirir. Stokastik kalkülüsn iki baskın versiyonu vardır, Itô stokastik kalkülüsü ve Stratonoviç stokastik kalkülüsü. İkisinin de avantajları ve dezavantajları vardır ve alana yeni aşina olmaya başlayanların belirli bir durumda hangisinin diğerinden daha uygun olduğu konusunda genellikle kafaları karışır. Bu konuda Øksendal (2003) gibi kılavuzlar mevcuttur. Aslında, bir Itô stokastik diferansiyel denklemini eşdeğer bir Stratonoviç stokastik diferansiyel denklemine ve tekrar geriye kolayca dönüştürebilmek mümkündür. Yine de, bir stokastik diferansiyel denklem ilk yazıldığında hangi tür kalkülüsün kullanılacağına dikkat edilmelidir.

Nümerik çözümler

Stokastik diferansiyel denklemleri sayısal çözmek için kullanılan yöntemler arasında Euler-Maruyama yöntemi, Milstein yöntemi, , ve yinelemeli stokastik integrallerin farklı temsillerine dayanan yöntemler yer almaktadır.

Fizikte kullanımı

Fizikte stokastik diferansiyel denklemler, moleküler dinamiklerden nörodinamiklere ve astrofizik nesnelerin dinamiklerine kadar geniş bir uygulama alanına sahiptir. Daha spesifik olarak,stokastik diferansiyel denklemlerler kuantum etkilerinin önemsiz olduğu veya bozulmalar olarak dikkate alınabildiği tüm dinamik sistemleri tanımlar. Stokastik diferansiyel denklemler dinamik sistemler teorisinin gürültülü modellere genelleştirilmesi olarak görülebilir. Bu önemli bir genellemedir; çünkü, gerçek sistemler çevrelerinden tamamen izole edilemez ve bu nedenle her zaman harici stokastik etki altındadırlar.

Yeni bilinmeyenler ekleyerek daha yüksek mertebeden denklemleri birkaç bağlı birinci mertebeden denkleme dönüştürmek için standart teknikler vardır. Bu nedenle, aşağıdakiler en genel stokastik diferansiyel denklemler sınıfıdır:

${\displaystyle {\frac {\mathrm {d} x(t)}{\mathrm {d} t}}=F(x(t))+\sum _{\alpha =1}^{n}g_{\alpha }(x(t))\xi ^{\alpha }(t),\,}$

Burada, ${\displaystyle x\in X}$ sistemin faz (veya durum) uzayındaki konumudur.

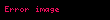
Olasılık ve finansal matematikteki kullanımı

Olasılık teorisinde (ve olasılık teorisinin örneğin filtreleme problemi ile sinyal işleme ve finansal matematik gibi uygulamalarında) kullanılan gösterim biraz farklıdır. Ayrıca, stokastik diferansiyel denklemleri çözmek için sayısal yöntemler üzerine yayınlarda kullanılan gösterimdir. Tipik bir denklem şu biçimdedir:

${\displaystyle \mathrm {d} X_{t}=\mu (X_{t},t)\,\mathrm {d} t+\sigma (X_{t},t)\,\mathrm {d} B_{t},}$

Burada, ${\displaystyle B}$ bir (standart Brown hareketi) belirtir. Aslında, bu şekilde yazılan bir denklem, alağıdaki gibi ifâde edilen bir integral denkleme karşık gelen kısa bir gösterim yolu olarak yorumlanmalıdır:

${\displaystyle X_{t+s}-X_{t}=\int _{t}^{t+s}\mu (X_{u},u)\mathrm {d} u+\int _{t}^{t+s}\sigma (X_{u},u)\,\mathrm {d} B_{u}.}$

Yukarıdaki denklem, stokastik süreç X_tnin davranışını, sıradan bir Lebesgue integralinin ve bir toplamı olarak karakterize eder. Stokastik diferansiyel denklemin sezgisel (ama çok yararlı) bir yorumu, δ uzunluğundaki küçük bir zaman aralığında stokastik süreç X_tnin değerini, beklenen değer μ(X_t, t) δ ve varyans σ(X_t, t)² δ ile normal dağılımlı bir miktarda değiştirmesi ve sürecin geçmiş davranışından bağımsız olmasıdır. Bunun nedeni, bir Wiener sürecinin artışlarının bağımsız ve normal dağılımlı olmasıdır. μ fonksiyonu sürüklenme katsayısı olarak adlandırılırken, σ difüzyon katsayısı olarak adlandırılır. Stokastik süreç X_t bir olarak adlandırılır ve sağlar.

Bir stokastik diferansiyel denklemin çözümünün iki ana tanımı vardır: güçlü çözüm ve zayıf çözüm. Her ikisi de SDE'nin integral denklem versiyonunu çözen bir süreç X_tnin varlığını gerektirir. İkisi arasındaki fark, üzerine dayandıkları (${\displaystyle \Omega ,\,{\mathcal {F}},\,P}$) olasılık uzayında bulunmaktadır. Zayıf çözüm, bir olasılık uzayından ve integral denklemi sağlayan bir süreçten oluşurken, güçlü çözüm, denklemi sağlayan ve belirli bir olasılık uzayında tanımlanan bir süreçtir. bu iki çözüm arasında bir bağlantı kurar.

Geometrik Brown hareketinin denklemi olan

${\displaystyle \mathrm {d} X_{t}=\mu X_{t}\,\mathrm {d} t+\sigma X_{t}\,\mathrm {d} B_{t}.}$

önemli bir örnektir ki bu denklem finansal matematikteki Black-Scholes opsiyon fiyatlandırma modelinde bir hisse senedinin fiyatının dinamiklerine ilişkin denklemdir.

Geometrik Brown hareketi genelleştirildiğinde, güçlü çözümlere izin veren ve dağılımı farklı geometrik Brown hareketleri veya Black Scholes modellerinden gelen yoğunlukların dışbükey bir bileşimi olan stokastik diferansiyel denklemleri tanımlamak da mümkündür ve çözümleri farklı Black Scholes modellerinin lognormal dağılımlarının bir karışım dinamiği olarak dağılan tek bir stokastik diferansiyel denklem elde edilir. Bu modelle birlikte, finansal matematikteki problemiyle başa çıkabilen modeller elde edilebilir.

(Aritmetik Brown hareketi) olarak adlandırılan daha basit bir stokastik diferansiyel denklem

${\displaystyle \mathrm {d} X_{t}=\mu \,\mathrm {d} t+\sigma \,\mathrm {d} B_{t}}$

1900 yılında tarafından hisse senedi fiyatları için ilk model olarak kullanılmış olup günümüzde olarak bilinmektedir.

Ayrıca, μ ve σ katsayılarının X_t sürecinin şimdiki değerine değil, aynı zamanda sürecin önceki değerlerine ve muhtemelen başka süreçlerin şimdiki veya önceki değerlerine de bağlı olduğu daha genel stokastik diferansiyel denklemler de vardır. Bu durumda çözüm süreci X, bir Markov süreci değildir. Bu durumda, bir olarak değil, bir olarak adlandırılır. Katsayılar, yalnızca X 'in şimdiki ve geçmiş değerlerine bağlı olduğunda, tanımlayıcı denklem stokastik gecikmeli diferansiyel denklem olarak adlandırılır.

Fisk-Stratonovich integraline sahip stokastik diferansiyel denklemlerin sıçramalı yarı martingallere genelleştirilmesi Marcus tipi stokastik diferansiyel denklemlerdir. Marcus integrali McShane'in stokastik hesabının bir uzantısıdır.

Stokastik finans alanında yenilikçi bir uygulama, için verilen stokastik diferansiyel denklemin kullanımından türemiştir:

${\displaystyle \mathrm {d} R_{t}=\mu R_{t}\,\mathrm {d} t+\sigma _{t}\,\mathrm {d} B_{t}.}$

Bu denklem getirilerin log-normal bir dağılım gösterdiği hipotezi altında bir hisse senedi fiyatı getirisinin dinamikleri için modellenmiş denklemdir. Bu hipotez altında, Marcello Minenna tarafından geliştirilen yöntemler, fenomenlerini gizleyebilecek anormal getiriyi tanımlayabilen tahmin aralığını belirler.

Kaynakça

1. ^ ^{a b c d e f} ; (2000). Diffusions, Markov Processes and Martingales, Vol 2: Ito Calculus. 2nd ed., Cambridge Mathematical Library. Cambridge University Press. doi:10.1017/CBO9780511805141. ISBN . OCLC 42874839. 
2. ^ ^{a b c} Musiela, M., and Rutkowski, M. (2004), Martingale Methods in Financial Modelling, 2nd Edition, Springer Verlag, Berlin.
3. ^ Kunita, H. (2004). Stochastic Differential Equations Based on Lévy Processes and Stochastic Flows of Diffeomorphisms. In: Rao, M.M. (eds) Real and Stochastic Analysis. Trends in Mathematics. Birkhäuser Boston. https://doi.org/10.1007/978-1-4612-2054-1_6
4. ^ Imkeller, Peter; Schmalfuss, Björn (2001). "The Conjugacy of Stochastic and Random Differential Equations and the Existence of Global Attractors". Journal of Dynamics and Differential Equations. 13 (2). ss. 215-249. doi:10.1023/a:1016673307045. ISSN 1040-7294. 7 Mart 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Aralık 2024. 
5. ^ ^{a b} Michel Emery (1989). Stochastic calculus in manifolds. Springer Berlin, Heidelberg. Doi https://doi.org/10.1007/978-3-642-75051-9
6. ^ Zdzisław Brzeźniak and , Stochastic differential equations on Banach manifolds, Methods Funct. Anal. Topology 6 (2000), no. 1, 43-84.
7. ^ Armstrong J. and (2018). Intrinsic stochastic differential equations as jets. Proc. R. Soc. A., 474: 20170559, http://doi.org/10.1098/rspa.2017.0559
8. ^ Akademik Bilim Terimleri Sözlüğü'nde Tedirgeme 6 Aralık 2024 tarihinde Wayback Machine sitesinde arşivlendi. maddesi
9. ^ ^{a b c d} (2003). Stochastic Differential Equations: An Introduction with Applications. Berlin: Springer. ISBN . 
10. ^ Armstrong, J., Brigo, D. and Rossi Ferrucci, E. (2019), Optimal approximation of SDEs on submanifolds: the Itô-vector and Itô-jet projections. Proc. London Math. Soc., 119: 176-213. https://doi.org/10.1112/plms.12226.
11. ^ Parisi, G.; Sourlas, N. (1979). "Random Magnetic Fields, Supersymmetry, and Negative Dimensions". Physical Review Letters. 43 (11). ss. 744-745. Bibcode:1979PhRvL..43..744P. doi:10.1103/PhysRevLett.43.744. 
12. ^ Kloeden, P.E., Platen E. (1992). Numerical Solution of Stochastic Differential Equations. Springer, Berlin, Heidelberg. DOI: https://doi.org/10.1007/978-3-662-12616-5
13. ^ Artemiev, S.S., Averina, T.A. (1997). Numerical Analysis of Systems of Ordinary and Stochastic Differential Equations. VSP, Utrecht, The Netherlands. DOI: https://doi.org/10.1515/9783110944662
14. ^ Kuznetsov, D.F. (2023). Strong approximation of iterated Itô and Stratonovich stochastic integrals: Method of generalized multiple Fourier series. Application to numerical integration of Itô SDEs and semilinear SPDEs. Differ. Uravn. Protsesy Upr., no. 1. DOI: https://doi.org/10.21638/11701/spbu35.2023.110
15. ^ Rybakov, K.A. (2023). Spectral representations of iterated stochastic integrals and their application for modeling nonlinear stochastic dynamics. Mathematics, vol. 11, 4047. DOI: https://doi.org/10.3390/math11194047
16. ^ Fengler, M. R. (2005), Semiparametric modeling of implied volatility, Springer Verlag, Berlin. DOI https://doi.org/10.1007/3-540-30591-2
17. ^ ; (2002). "Lognormal-mixture dynamics and calibration to market volatility smiles". International Journal of Theoretical and Applied Finance. 5 (4): 427-446. doi:10.1142/S0219024902001511. 
18. ^ Brigo, D, Mercurio, F, Sartorelli, G. (2003). Alternative asset-price dynamics and volatility smile, QUANT FINANC, 2003, Vol: 3, Pages: 173 - 183, ISSN 1469-7688
19. ^ Steven Marcus (1981), "Modeling and approximation of stochastic differential equation driven by semimartigales", Stochastics, 4, ss. 223-245 
20. ^ "Detecting Market Abuse". Risk Magazine. 2 Kasım 2004. 18 Mayıs 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Aralık 2024. 
21. ^ "The detection of Market Abuse on financial markets: a quantitative approach". Consob – The Italian Securities and Exchange Commission. 21 Mart 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Aralık 2024.