Matematikte sınır değer problemleri, sınır koşulları ile verilen diferansiyel denklemlerdir. Bir sınır değer probleminin çözümü, verilen diferansiyel denklemin uygun sınır koşullarına uyum sağlayan çözümüdür.

Sınır değer problemlerine fizik ve mühendislikte sıkça karşılaşılır. Bunlara örnek olarak Laplace denklemi kullanılarak elektrik potansiyelinin bulunması, dalga denklemi ile bir sistemin normal modlarının hesaplanması ve ısı denklemi ile bir çubukta ısının dağılımının çözülmesi örnek verilebilir. Sınır değer problemlerinin büyük çoğunluğu Sturm–Liouville problemi cinsindedir; bu problemlerde diferansiyel operatörünün özdeğerinin incelenmesi gerekir. Sınır değer problemlerinin fiziksel olarak anlamlı olabilmesi için bu problemlerin "iyi tanımlanmış" (well-posed) olması gerekir: iyi tanımlanmış problemlerin bu sınır koşulları için tek bir özgün çözümünün olması ve bu çozümün stabil ve sürekli olması beklenir.
Sınır değerleri


Çözülmek istenilen sistemin gerekliliklerine göre farklı sınır koşulları kullanılır. En yaygın sınır koşullarından bazıları Dirichlet ve Neumann sınır koşullarıdır. Dirichlet sınır koşulunda denklemin çözüldüğü sınırlar bir fonksiyon değerlerine eşitlenirken, Neumann'da çözümün türevi eşitlenir.
Sınır koşulları, başlangıç koşulları ile karıştırılmamalıdır.
Sıkça kullanılan sınır değerlerinin özeti aşağıdaki tabloda verilmiştir. 

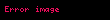


| İsim | Sınırın 1. kısmı | Sınırın 2. kısmı |
|---|---|---|
| Dirichlet | 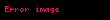 | |
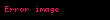 | ||
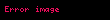 | ||
 |  | |
both  , and , and  | ||
Ayrıca bakınız
Kaynakça
- ^ Zwillinger, Daniel (2014). Handbook of differential equations (İngilizce). Elsevier Science. s. 536. ISBN .
- ^ a b Anar, İbrahim Ethem (2005). Kısmi diferansiyel denklemler. Ankara: Palme. ISBN .
- ^ a b Strauss, Walter A. (1992). Partial differential equations: an introduction (İngilizce). New York: Wiley. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte sinir deger problemleri sinir kosullari ile verilen diferansiyel denklemlerdir Bir sinir deger probleminin cozumu verilen diferansiyel denklemin uygun sinir kosullarina uyum saglayan cozumudur Bir diferansiyel denklemin cozuldugu alan ve sinirlari Sinir deger problemlerine fizik ve muhendislikte sikca karsilasilir Bunlara ornek olarak Laplace denklemi kullanilarak elektrik potansiyelinin bulunmasi dalga denklemi ile bir sistemin normal modlarinin hesaplanmasi ve isi denklemi ile bir cubukta isinin dagiliminin cozulmesi ornek verilebilir Sinir deger problemlerinin buyuk cogunlugu Sturm Liouville problemi cinsindedir bu problemlerde diferansiyel operatorunun ozdegerinin incelenmesi gerekir Sinir deger problemlerinin fiziksel olarak anlamli olabilmesi icin bu problemlerin iyi tanimlanmis well posed olmasi gerekir iyi tanimlanmis problemlerin bu sinir kosullari icin tek bir ozgun cozumunun olmasi ve bu cozumun stabil ve surekli olmasi beklenir Sinir degerleriTek boyutlu isi denklemini semasiTek boyutlu isi denkleminin bir cubuk icin cozumu Bu cozumde Neumann sinir kosullari kullanilmistir ve baslangic degerleri olarak cubugun sol tarafi sicak ve sag tarafi soguk olarak alinmistir Cozulmek istenilen sistemin gerekliliklerine gore farkli sinir kosullari kullanilir En yaygin sinir kosullarindan bazilari Dirichlet ve Neumann sinir kosullaridir Dirichlet sinir kosulunda denklemin cozuldugu sinirlar bir fonksiyon degerlerine esitlenirken Neumann da cozumun turevi esitlenir Sinir kosullari baslangic kosullari ile karistirilmamalidir Sikca kullanilan sinir degerlerinin ozeti asagidaki tabloda verilmistir y displaystyle y bilinmeyen fonksiyona cozum c0 displaystyle c 0 ile c1 displaystyle c 1 kosullarin sabitlerine ve f displaystyle f ile g displaystyle g ise bilinen skalar fonksiyonlara tekabul eder Isim Sinirin 1 kismi Sinirin 2 kismiDirichlet y f displaystyle y f y n f displaystyle partial y over partial n f c0y c1 y n f displaystyle c 0 y c 1 partial y over partial n f y f displaystyle y f c0y c1 y n f displaystyle c 0 y c 1 partial y over partial n f both y f displaystyle y f and c0 y n g displaystyle c 0 partial y over partial n g Ayrica bakinizAdi diferansiyel denklemler Kismi diferansiyel denklemlerKaynakca Zwillinger Daniel 2014 Handbook of differential equations Ingilizce Elsevier Science s 536 ISBN 978 1 4832 2096 3 a b Anar Ibrahim Ethem 2005 Kismi diferansiyel denklemler Ankara Palme ISBN 975 8982 19 2 erisim tarihi kullanmak icin url gerekiyor yardim a b Strauss Walter A 1992 Partial differential equations an introduction Ingilizce New York Wiley ISBN 978 0470054567
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State