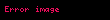Titius-Bode yasası (ya da yalnızca Bode yasası) Güneş Sistemi'nde bulunan gezegenlerin yarı büyük eksenlerinin basit bir kurala dayandığını ileri süren bir varsayımdır. 1846 yılında Neptün'ün bulunmasıyla geçersiz kalmıştır. Yasa adını Johann Daniel Titus (1729-1796) ve Johann Elert Bode (1747-1826) adlı iki Alman astronomundan almıştır. Titus kuralı ortaya koymuş, Bode ise kuralın bilim dünyasınca tanınmasını sağlamıştır.
Gezegen kavramı
Antik çağlardan beri gezegenlerin varlığı bilinirdi. Antik çağda çıplak gözle görünen ve gökyüzündeki hareketleri arka plan yıldızlardan farklı olan yedi cisim gezegen (planet) olarak adlandırılıyordu. Bunlar, Güneş, Ay, Merkür, Venüs, Mars, Jüpiter ve Saturn'dü. Copernicus'un Güneş merkezli evren modelinden sonra Dünya'nın gezegen olduğu, buna karşılık Güneş ve Ay'ın gezegen olmadığı anlaşıldı. Bu altı cismin yörüngeleri de hesaplandı.
Gezegen yörüngeleri
Gezegen yörüngeleri elips şeklindedir. Ancak elips dış merkezliği genellikle 0 a yakındır. Yani elipler (bir ölçüde Merkür hariç) çembere yakındır Bu elipslerin yarı büyük eksenleri ölçülmüştür. (Elipsteki yarı büyük eksen çamberdeki yarıçapın karşılığıdır) Mesela Dünyanın yarı büyük ekseni 149.6 milyon kilometredir. Tabloda "Güneş'e uzaklık başlığı altında yarı büyük eksenler gösterilmiştir. 18. yüzyılda bazı astronomlar Dünya'nın Güneş'e olan uzaklığını 10 birim kabul ederek diğer gezegenlerin yarı büyük eksenlerini bu ölçü birimiyle de ölçtüler. Tabloda bu 18. yüzyılda bilinen altı gezegenin yarı büyük eksenleri bu ölçü birimiyle de gösterilmiştir.
| Gezegen | Güneş'e uzaklık (milyon kilometre) | Güneş'e uzaklık (Dünya uzaklığının 1/10 u cinsinden) |
|---|---|---|
| Merkür | 57.9 | 3.9 |
| Venüs | 108.2 | 7.2 |
| Dünya | 149.6 | 10 |
| Mars | 227.99 | 15.2 |
| Jupiter | 778.6 | 52.0 |
| Saturn | 1433.5 | 95.8 |
Yasanın ortaya çıkışı

Gezegen yörüngelerinin gezegenlerin birbirlerine olan etkisi sebebiyle zaman içinde biraz değiştiği varsayıldığı için Titus küsuratlı rakamları tam sayıya tamamladı ve 1766 yılında yörünge yarı büyük eksenleri için bir seri oluşturdu: Bu seri 4,7,10,16,52 ve 96 sayılarından oluşuyordu. Serideki bu rakamlar arasında şöyle bir ilişki kurdu:
- Merkür :4+0=4
- Venüs :4+3*1=4+3*20=7 birim
- Dünya 4+3*2=4+3*21=10 birim
- Mars: 4+3*4=4+3*22=16 birim
- Jüpiter:4+3*16=4+3*24=52 birim
- Saturn:4+3*32=4+3*25=100 birim
ya da matematik denklemiyle; Venüs ve sonraki gezegenler için;
Burada a yarı büyük eksen, m gezegenin 2. gezegen Venüs^ten başlamak kaydıyla Güneşe yakınlık sıradır. Bu matematiksel ilişki ilginç bulunmakla birlikte Mars ve Jüpiter arasındaki uyumsuzluk, yani 4+3*23 yarı büyük ekseninde bir gezegenin olmaması sebeiyle fazla inandırıcı bulunmuyordu. Ancak üst üste gelen iki keşif durumu değiştirdi.
- 1781 yılında Uranüs gezegeni keşfedildi. Uranüs yarı büyük ekseni 2872.5 milyon kilometre yani 192.2 birimdir.
- Uranüs:4+3*26=196 birim
1801 yılında (yani Tütus'un ölümünden sonra) Ceres cüce gezegeni bulundu. Ceres yarı büyük ekseni 414 milyon kilometre yani 27.68 birimdir
- Ceres:4+3*23 =28 Birim
Özetle
| Gezegen | Bode Titus yasasına göre Yarı büyük eksen | Ölçülen yarı büyük eksen | Sapma |
|---|---|---|---|
| Merkür | 4 | 3.87 | %3 |
| venüs | 7 | 7.23 | %3 |
| Dünya | 10 | 10 | - |
| Mars | 16 | 15.24 | %5 |
| ceres | 28 | 27.68 | % 1 |
| Jüpiter | 52 | 52.04 | 0 |
| saturn | 100 | 96 | % 4 |
| Uranüs | 196 | 192.2 | % 4 |
Matematiksel ifadesi
Yasaya göre Güneş'ten dışarı doğru her gezegenin a ile ifade edilen yarı büyük ekseni, Dünya'nın yarı büyük ekseni = 10 olacak şekilde birimlerle gösterildiğinde
n = 0, 3, 6, 12, 24, 48 ..., gibi n'in 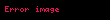
= 0.4 + 0.3 · 2 m
m = 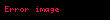
Dış gezegenler için, her gezegenin kabaca bir önceki gezegenin Güneş'ten olan uzaklığının iki katı kadar uzakta olduğu tahmin edilir.
Basit anlatımı
Berlin’li astronom “”ye göre, gezegenler uzayda tesadüfi olarak konumlanmamışlardır. Onların güneşe olan uzaklıkları, kendi keşfettiği belirgin bir kurala bağlıdır.
- Şöyle ki
- Sıfırdan başlayarak, takip eden ilk sayı 3 olarak alınır. Sonraki her bir sayı, bir öncekinin iki katı olmak üzere toplam 8 adet sayı belirlenir:
| Seçilen sayılar | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 3 | 6 | 12 | 24 | 48 | 96 | 192 |
Bu sayıların her birine 4 ilave edilir:
| Seçilen sayılar + 4 | |||||||
|---|---|---|---|---|---|---|---|
| 4 | 7 | 10 | 16 | 28 | 52 | 100 | 196 |
Bulunan sayıların her biri 10'a bölünür:
| (Seçilen sayılar + 4) / 10 | |||||||
|---|---|---|---|---|---|---|---|
| 0,4 | 0,7 | 1,0 | 1,6 | 2,8 | 5,2 | 10,0 | 19,6 |
Elde edilen bu sayılardan 1 sayısı dünyanın güneşe uzaklığı olarak kabul edilirse, diğer sayılar diğer gezegenlerin güneşe yaklaşık uzaklığını verir.
Gezegenlerin güneşe gerçek uzaklıkları ise şöyledir:
| Gezegenlerin güneşe olan gerçek uzaklıkları | |||||||
|---|---|---|---|---|---|---|---|
| 0,3870 | 0,7233 | 1 | 1,5236 | - - - - | 5,2028 | 9,5388 | 19,1832 |
| Merkür | Venüs | Dünya | Mars | - - - - | Jüpiter | Satürn | Uranüs |
Yasanın sonu
Bir süre için daha sonra keşfedilecek gezegenlerin de bu kurala uyacağı varsayıldı. Ancak bu beklenti boş çıktı. 1846 yılında Neptün gezegeni keşfedildi. Ama beklentinin aksine bu gezegenin yarı büyük ekseni 4+3*27=388 birim değil, 301.1 birimdi. Sapma % 26 ydı. 20. yüzyılda Kupier kuşağındaki Pluto, Eris vb çeşitli cüce gezegenler keşfedilince hiç birinin yarı büyük ekseninin Bode Titus kuralına uymadığı ortaya çıktı.
Notlar
- ^ "NASA Gezegen tablosu (İngilizce)". 26 Ağustos 2019 tarihinde kaynağından . Erişim tarihi: 7 Mart 2019.
- ^ Isaac Asimov:Biographical Encyclopaedia of Science and Technology sf 290
- ^ (PDF). Wartburg College. 27 Mart 2009 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 8 Kasım 2007.
- ^ Mon Professeur, GRANDE ENCYCLOPÉDIE AUTODIDACTIQUE MODERNE ILLUSTRÉE, TOME PREMIER, Paris. Cilt 1, Sayfa 122
- ^ 1900'lü yılların başında (1910'dan az sonra) basılmış "Mon Professeur" adlı Fransızca ansiklopedideki değerlerdir.
 | Astronomi ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Titius Bode yasasi ya da yalnizca Bode yasasi Gunes Sistemi nde bulunan gezegenlerin yari buyuk eksenlerinin basit bir kurala dayandigini ileri suren bir varsayimdir 1846 yilinda Neptun un bulunmasiyla gecersiz kalmistir Yasa adini Johann Daniel Titus 1729 1796 ve Johann Elert Bode 1747 1826 adli iki Alman astronomundan almistir Titus kurali ortaya koymus Bode ise kuralin bilim dunyasinca taninmasini saglamistir Gezegen kavramiAntik caglardan beri gezegenlerin varligi bilinirdi Antik cagda ciplak gozle gorunen ve gokyuzundeki hareketleri arka plan yildizlardan farkli olan yedi cisim gezegen planet olarak adlandiriliyordu Bunlar Gunes Ay Merkur Venus Mars Jupiter ve Saturn du Copernicus un Gunes merkezli evren modelinden sonra Dunya nin gezegen oldugu buna karsilik Gunes ve Ay in gezegen olmadigi anlasildi Bu alti cismin yorungeleri de hesaplandi Gezegen yorungeleriGezegen yorungeleri elips seklindedir Ancak elips dis merkezligi genellikle 0 a yakindir Yani elipler bir olcude Merkur haric cembere yakindir Bu elipslerin yari buyuk eksenleri olculmustur Elipsteki yari buyuk eksen camberdeki yaricapin karsiligidir Mesela Dunyanin yari buyuk ekseni 149 6 milyon kilometredir Tabloda Gunes e uzaklik basligi altinda yari buyuk eksenler gosterilmistir 18 yuzyilda bazi astronomlar Dunya nin Gunes e olan uzakligini 10 birim kabul ederek diger gezegenlerin yari buyuk eksenlerini bu olcu birimiyle de olctuler Tabloda bu 18 yuzyilda bilinen alti gezegenin yari buyuk eksenleri bu olcu birimiyle de gosterilmistir Gezegen Gunes e uzaklik milyon kilometre Gunes e uzaklik Dunya uzakliginin 1 10 u cinsinden Merkur 57 9 3 9Venus 108 2 7 2Dunya 149 6 10Mars 227 99 15 2Jupiter 778 6 52 0Saturn 1433 5 95 8Yasanin ortaya cikisiBu grafikte gezegenlerin gercek uzakliklari mavi ve Bode Titus yasasina gore hesaplanan uzakliklari kirmizi gorunmektedir Gezegen yorungelerinin gezegenlerin birbirlerine olan etkisi sebebiyle zaman icinde biraz degistigi varsayildigi icin Titus kusuratli rakamlari tam sayiya tamamladi ve 1766 yilinda yorunge yari buyuk eksenleri icin bir seri olusturdu Bu seri 4 7 10 16 52 ve 96 sayilarindan olusuyordu Serideki bu rakamlar arasinda soyle bir iliski kurdu Merkur 4 0 4 Venus 4 3 1 4 3 20 7 birim Dunya 4 3 2 4 3 21 10 birim Mars 4 3 4 4 3 22 16 birim Jupiter 4 3 16 4 3 24 52 birim Saturn 4 3 32 4 3 25 100 birim ya da matematik denklemiyle Venus ve sonraki gezegenler icin a 4 3 2m displaystyle a 4 3 times 2 m dd Burada a yari buyuk eksen m gezegenin 2 gezegen Venus ten baslamak kaydiyla Gunese yakinlik siradir Bu matematiksel iliski ilginc bulunmakla birlikte Mars ve Jupiter arasindaki uyumsuzluk yani 4 3 23 yari buyuk ekseninde bir gezegenin olmamasi sebeiyle fazla inandirici bulunmuyordu Ancak ust uste gelen iki kesif durumu degistirdi 1781 yilinda Uranus gezegeni kesfedildi Uranus yari buyuk ekseni 2872 5 milyon kilometre yani 192 2 birimdir Uranus 4 3 26 196 birim 1801 yilinda yani Tutus un olumunden sonra Ceres cuce gezegeni bulundu Ceres yari buyuk ekseni 414 milyon kilometre yani 27 68 birimdir Ceres 4 3 23 28 Birim Ozetle Gezegen Bode Titus yasasina gore Yari buyuk eksen Olculen yari buyuk eksen SapmaMerkur 4 3 87 3venus 7 7 23 3Dunya 10 10 Mars 16 15 24 5ceres 28 27 68 1Jupiter 52 52 04 0saturn 100 96 4Uranus 196 192 2 4Matematiksel ifadesiYasaya gore Gunes ten disari dogru her gezegenin a ile ifade edilen yari buyuk ekseni Dunya nin yari buyuk ekseni 10 olacak sekilde birimlerle gosterildiginde a n 4 displaystyle a n 4 n 0 3 6 12 24 48 gibi n in n gt 3 displaystyle n gt 3 degerleri icin bir oncekinin iki kati olacak degerler alir Elde edilen degerler 10 a bolunerek gok birimine GB cevrilir ve su ifade de kullanilir a displaystyle a 0 4 0 3 2 m m displaystyle displaystyle infty 0 1 2 Dis gezegenler icin her gezegenin kabaca bir onceki gezegenin Gunes ten olan uzakliginin iki kati kadar uzakta oldugu tahmin edilir Basit anlatimiBerlin li astronom ye gore gezegenler uzayda tesadufi olarak konumlanmamislardir Onlarin gunese olan uzakliklari kendi kesfettigi belirgin bir kurala baglidir Soyle ki Sifirdan baslayarak takip eden ilk sayi 3 olarak alinir Sonraki her bir sayi bir oncekinin iki kati olmak uzere toplam 8 adet sayi belirlenir Secilen sayilar0 3 6 12 24 48 96 192 Bu sayilarin her birine 4 ilave edilir Secilen sayilar 44 7 10 16 28 52 100 196 Bulunan sayilarin her biri 10 a bolunur Secilen sayilar 4 100 4 0 7 1 0 1 6 2 8 5 2 10 0 19 6 Elde edilen bu sayilardan 1 sayisi dunyanin gunese uzakligi olarak kabul edilirse diger sayilar diger gezegenlerin gunese yaklasik uzakligini verir Gezegenlerin gunese gercek uzakliklari ise soyledir Gezegenlerin gunese olan gercek uzakliklari0 3870 0 7233 1 1 5236 5 2028 9 5388 19 1832Merkur Venus Dunya Mars Jupiter Saturn UranusYasanin sonuBir sure icin daha sonra kesfedilecek gezegenlerin de bu kurala uyacagi varsayildi Ancak bu beklenti bos cikti 1846 yilinda Neptun gezegeni kesfedildi Ama beklentinin aksine bu gezegenin yari buyuk ekseni 4 3 27 388 birim degil 301 1 birimdi Sapma 26 ydi 20 yuzyilda Kupier kusagindaki Pluto Eris vb cesitli cuce gezegenler kesfedilince hic birinin yari buyuk ekseninin Bode Titus kuralina uymadigi ortaya cikti Notlar NASA Gezegen tablosu Ingilizce 26 Agustos 2019 tarihinde kaynagindan Erisim tarihi 7 Mart 2019 Isaac Asimov Biographical Encyclopaedia of Science and Technology ISBN 0 330 24322 3 sf 290 PDF Wartburg College 27 Mart 2009 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 8 Kasim 2007 Mon Professeur GRANDE ENCYCLOPEDIE AUTODIDACTIQUE MODERNE ILLUSTREE TOME PREMIER Paris Cilt 1 Sayfa 122 1900 lu yillarin basinda 1910 dan az sonra basilmis Mon Professeur adli Fransizca ansiklopedideki degerlerdir Astronomi ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans