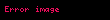Matematikte, uzunluğu 1 (birim uzunluğu) olan ve uzayda bir norma sahip olan vektöre birim vektör denir. Birim vektör genellikle ‘û‘ gibi şapkalı ve küçük harflerle ifade edilir. Normalize vektör veya versor olmayan bir sıfır vektörü u ile eş yönlü olan birim vektörü u
Mutlak u,u vektörünün normunu (veya uzunluğunu) verir. Bu normalize vektör bazen birim vektörün eş anlamı olarak da kullanılır. Bir kaynağın veya bir ilkenin elementleri birim vektör olmak üzere seçilebilir. Uzaydaki her vektör birim vektörün linear bileşenleri olarak yazılabilir. En çok rastlanılan kaynaklar Kartezyen, polar ve küresel koordinatlarıdır. Her biri, koordinat sisteminin simetrisine göre farklı birim vektörleri kullanır. Bu sistemler çok farklı içeriklere sahip oldukları için burada kullanıldıklarından daha farklı bir kullanıma rastalamak pek yaygın değildir. Tanım olarak, Öklid geometrisi’nde iki birim vektörün nokta çarpımı basitçe aralarındaki açının cosinüsüdür. Üç boyutlu Öklid geometrisi’nde ise, iki dikey birim vektörün çapraz çarpımı diğer bir birim vektöre eşittir.
Dikey koordinatlar
Kartezyen koordinatlar
Birim vektörler, Kartezyen koordinat sisteminin eksenlerini ifade etmek için de kullanılabilir. Örneğin, üç boyutlu x,y,z eksenlerinde eş yönlü birim vektörün Kartezyen koordinat sistemi;
Bazen Versor’un koordinat sistemi olarak da bahsedilir. Genellikle, standart birim vektör işaretlerinden() farklı olarak normal vektör işaretleri (i ya da) ile gösterilirler. Birçok yerde i,j i, j, k, ve(






Silindirik koordinatlar
Silindirsel simetri için uygun üç dikey birim vektör vardır. Bunlar; 







=
=




Küresel koordinatlar
Küresel bir simetriye uygun birim vektörleri: 


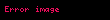



Küresel birim vektörler hem 

Genel birim vektörler
Fizik ve Geometri boyunca meydana gelen birim vektörlerin ortak genel temaları:
| Birim vektör | Terimleme | Diyagram |
|---|---|---|
| Bir eğri çizgisine teğet vektör |  |   Bir düzlemin içerdiği normal vektörü |
| Radyal konum bileşeni ve açısal teğet bileşeni içeren bir yüzeye teğet normal düzlemi |  açısından açısından ; | |
| Binormal tanjant vektör ve normal |  | |
| Bazı eksen /hattına paralel |  |  Bir birim vektörü |
| Bir radyal doğrultuda bir eksen/hattına dik |  | |
| Bazı eksen/hattına bağlı mümkün açısal sapma |  |  Akut sapma açısında φ birim vektörü (0 or π/2 rad dahil olmak üzere) göreceli bir yöne göre belirlenir. |
Eğrisel koordinatlar
Genellikle, koordinat sistemi benzersiz bir vektör numarası kullanılarak belirtilebilir. Bağımsız birim vektörleri 




Kaynakça
- İngilizce vikipedi24 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte uzunlugu 1 birim uzunlugu olan ve uzayda bir norma sahip olan vektore birim vektor denir Birim vektor genellikle u gibi sapkali ve kucuk harflerle ifade edilir Normalize vektor veya versor olmayan bir sifir vektoru u ile es yonlu olan birim vektoru u u u u displaystyle mathbf hat u frac mathbf u mathbf u Mutlak u u vektorunun normunu veya uzunlugunu verir Bu normalize vektor bazen birim vektorun es anlami olarak da kullanilir Bir kaynagin veya bir ilkenin elementleri birim vektor olmak uzere secilebilir Uzaydaki her vektor birim vektorun linear bilesenleri olarak yazilabilir En cok rastlanilan kaynaklar Kartezyen polar ve kuresel koordinatlaridir Her biri koordinat sisteminin simetrisine gore farkli birim vektorleri kullanir Bu sistemler cok farkli iceriklere sahip olduklari icin burada kullanildiklarindan daha farkli bir kullanima rastalamak pek yaygin degildir Tanim olarak Oklid geometrisi nde iki birim vektorun nokta carpimi basitce aralarindaki acinin cosinusudur Uc boyutlu Oklid geometrisi nde ise iki dikey birim vektorun capraz carpimi diger bir birim vektore esittir Dikey koordinatlarKartezyen koordinatlarBirim vektorler Kartezyen koordinat sisteminin eksenlerini ifade etmek icin de kullanilabilir Ornegin uc boyutlu x y z eksenlerinde es yonlu birim vektorun Kartezyen koordinat sistemi i 100 j 010 k 001 displaystyle mathbf hat i begin bmatrix 1 0 0 end bmatrix mathbf hat j begin bmatrix 0 1 0 end bmatrix mathbf hat k begin bmatrix 0 0 1 end bmatrix Bazen Versor un koordinat sistemi olarak da bahsedilir Genellikle standart birim vektor isaretlerinden farkli olarak normal vektor isaretleri i ya da ile gosterilirler Bircok yerde i j i j k ve i displaystyle vec imath ȷ displaystyle vec jmath ve k displaystyle vec k 3D Kartezyen koordinat sisteminin versorlari olarak varsayilabilir Ayrica bu isaretler x y z displaystyle mathbf hat x mathbf hat y mathbf hat z x 1 x 2 x 3 displaystyle mathbf hat x 1 mathbf hat x 2 mathbf hat x 3 e x e y e z displaystyle mathbf hat e x mathbf hat e y mathbf hat e z or e 1 e 2 e 3 displaystyle mathbf hat e 1 mathbf hat e 2 mathbf hat e 3 sapkali veya sapkasiz olarak kullanilir Kaynaklarda ozellikle i j k baska bir nicelige sahip olan bir karisikliga sebep olabilir ornegin i j k gibi icerik sembolleri bir takimin elementleri sirasi veya cesitlilik dizisi olarak tanimlanabilir Uzaydaki bir birim vektor i j k nin cizgisel kombinasyonlari olarak kartezyen sembolleri ile ifade edildiginde bu uc bilesen kosinus fonksiyonun yonu olarak tanimlanabilir Her bir bilesenin degeri ayri ayri vektorle birim vektorun arasinda olusturduklari acinin kosinusune esittir Duz bir cizginin cizginin bir kisminin acisal eksenlerinin veya acisal eksenlerin bir parcasinin tanimlamak icin kullanilan yontemlerden bir tanesidir Silindirik koordinatlarSilindirsel simetri icin uygun uc dikey birim vektor vardir Bunlar s displaystyle mathbf hat s ayrica bunlar da kullanilabilir e displaystyle mathbf hat e ya da r displaystyle boldsymbol hat rho noktanin simetri ekseninden olan uzakligini gosterir f displaystyle boldsymbol hat varphi saat yonunu tersinde hareket ederse hareket yonunun gozlemlenebildigine karsilik gelmektedir z displaystyle mathbf hat z simetri ekseninin yonune karsilik gelir Bunlar kartezyenin temeli olan x displaystyle hat x y displaystyle hat y z displaystyle hat z ile iliskilendirilir s displaystyle mathbf hat s cos fx sin fy displaystyle cos varphi mathbf hat x sin varphi mathbf hat y f displaystyle boldsymbol hat varphi sin fx cos fy displaystyle sin varphi mathbf hat x cos varphi mathbf hat y z z displaystyle mathbf hat z mathbf hat z s displaystyle mathbf hat s vef displaystyle boldsymbol hat varphi f displaystyle varphi nin fonksiyonlari oldugunu belirtmek onemlidir ve sabit bir yonleri yoktur Silindirik koordinatlarda turevleyerek ve integralini alarak bu vektorleri calistirabiliriz Daha eksiksiz bir aciklama icin Jacobian matrix e bakiniz Fonksiyonun f displaystyle varphi turevleri sunlardir s f sin fx cos fy f displaystyle frac partial mathbf hat s partial varphi sin varphi mathbf hat x cos varphi mathbf hat y boldsymbol hat varphi f f cos fx sin fy s displaystyle frac partial boldsymbol hat varphi partial varphi cos varphi mathbf hat x sin varphi mathbf hat y mathbf hat s z f 0 displaystyle frac partial mathbf hat z partial varphi mathbf 0 Kuresel koordinatlarKuresel bir simetriye uygun birim vektorleri r displaystyle mathbf hat r orjinden artan radyal uzunlugun yonu f displaystyle boldsymbol hat varphi x y duzleminde saat yonunun tersi yonde gelen pozitif x ekseni artmaktadir ve 8 displaystyle boldsymbol hat theta z ekseni yonundeki pozitif gelen aci artmaktadir Bozulmayi cakisikligi en aza indirmek icin polar aci genellikle 0 8 180 displaystyle 0 leq theta leq 180 circ alinir Siklikla f displaystyle boldsymbol hat varphi ve 8 displaystyle boldsymbol hat theta gosterilen kuresel koordinatlarda yazilmis herhangi bir duzen uclu baglamina dikkat etmek ozellikle onemlidir Amerikan fizik kongresinde de kullanilmistir Bu azimutal aci yaparak f displaystyle varphi silindir koordinatlar da bunun aynisi olarak tanimlanir Kartezyen iliskileri sunlardir r sin 8cos fx sin 8sin fy cos 8z displaystyle mathbf hat r sin theta cos varphi mathbf hat x sin theta sin varphi mathbf hat y cos theta mathbf hat z 8 cos 8cos fx cos 8sin fy sin 8z displaystyle boldsymbol hat theta cos theta cos varphi mathbf hat x cos theta sin varphi mathbf hat y sin theta mathbf hat z f sin fx cos fy displaystyle boldsymbol hat varphi sin varphi mathbf hat x cos varphi mathbf hat y Kuresel birim vektorler hem f displaystyle varphi hem 8 displaystyle theta a baglidir ve dolayisiyla bes tane sifir olmayan turevleri vardir Daha eksiksiz bir aciklama icin Jakobien bakiniz Sifir olmayan turevleri r f sin 8sin fx sin 8cos fy sin 8f displaystyle frac partial mathbf hat r partial varphi sin theta sin varphi mathbf hat x sin theta cos varphi mathbf hat y sin theta boldsymbol hat varphi r 8 cos 8cos fx cos 8sin fy sin 8z 8 displaystyle frac partial mathbf hat r partial theta cos theta cos varphi mathbf hat x cos theta sin varphi mathbf hat y sin theta mathbf hat z boldsymbol hat theta 8 f cos 8sin fx cos 8cos fy cos 8f displaystyle frac partial boldsymbol hat theta partial varphi cos theta sin varphi mathbf hat x cos theta cos varphi mathbf hat y cos theta boldsymbol hat varphi 8 8 sin 8cos fx sin 8sin fy cos 8z r displaystyle frac partial boldsymbol hat theta partial theta sin theta cos varphi mathbf hat x sin theta sin varphi mathbf hat y cos theta mathbf hat z mathbf hat r f f cos fx sin fy sin 8r cos 88 displaystyle frac partial boldsymbol hat varphi partial varphi cos varphi mathbf hat x sin varphi mathbf hat y sin theta mathbf hat r cos theta boldsymbol hat theta Genel birim vektorler Fizik ve Geometri boyunca meydana gelen birim vektorlerin ortak genel temalari Birim vektor Terimleme DiyagramBir egri cizgisine teget vektor t displaystyle mathbf hat t Bir duzlemin icerdigi normal vektoru n displaystyle mathbf hat n ve radyal pozisyon vektoru rr displaystyle r mathbf hat r tarafindan tanimlanan ve acisal tegeti donme dogrultusu 88 displaystyle theta boldsymbol hat theta vektor denklemlerinin acisal hareketlerinin bulunmasi icin gereklidir Radyal konum bileseni ve acisal teget bileseni iceren bir yuzeye teget normal duzlemi n displaystyle mathbf hat n acisindan n r 8 displaystyle mathbf hat n mathbf hat r times boldsymbol hat theta Binormal tanjant vektor ve normal b t n displaystyle mathbf hat b mathbf hat t times mathbf hat n Bazi eksen hattina paralel e displaystyle mathbf hat e parallel Bir birim vektorue displaystyle mathbf hat e parallel bir ana dogrultuda kirmizi cizgi paralel hizalanmis ve ona dik birim vektor e displaystyle mathbf hat e bot herhangi bir radyal dogrultuda ana hattina goredir Bir radyal dogrultuda bir eksen hattina dik e displaystyle mathbf hat e bot Bazi eksen hattina bagli mumkun acisal sapma e displaystyle mathbf hat e angle Akut sapma acisinda f birim vektoru 0 or p 2 rad dahil olmak uzere goreceli bir yone gore belirlenir Egrisel koordinatlarGenellikle koordinat sistemi benzersiz bir vektor numarasi kullanilarak belirtilebilir Bagimsiz birim vektorleri e n displaystyle mathbf hat e n uzayin serbestlik derecesine esittir Siradan 3 uzayi icin bu vektorler e 1 e 2 e 3 displaystyle mathbf hat e 1 mathbf hat e 2 mathbf hat e 3 ifade edilebilir Bu sistemi tanimlamak ve ortonormal olmak icin her zaman uygun olan denklemler e i e j dij displaystyle mathbf hat e i cdot mathbf hat e j delta ij e i e j e k eijk displaystyle mathbf hat e i cdot mathbf hat e j times mathbf hat e k varepsilon ijk dijKronecker delta dir i j dir ve sifirdan farklidir ve eijk displaystyle varepsilon ijk permutasyon duzenlerinin bir tanesidir ijk ve eksi sirali permutasyonukji Kaynakca M R Spiegel S Lipschutz D Spellman 2009 Vector Analysis Schaum s Outlines Series 2 bas Mc Graw Hill ISBN 978 0 07 161545 7 KB1 bakim Birden fazla ad yazar listesi link Ingilizce vikipedi24 Ekim 2014 tarihinde Wayback Machine sitesinde arsivlendi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans