Vakum geçirgenliği

Fiziksel sabit ε₀, yaygın olarak vakum geçirgenliği, serbest uzayın geçirgenliği veya elektrik sabiti olarak adlandırılır. Bu ideal fiziksel sabit klasik vakumun dielektrik sabitinin mutlak değeridir. e0 sabitinin sayısal değeri:

e₀ = 8.854 187 817... × 10^-12 F·m^-1 (metre başına farad).

Vakum ortamı, elektrik alan çizgilerinin geçmesine izin verme özelliğine sahiptir. e0 sabiti, uzunluk ve güç gibi mekanik miktarlarda, elektrik yükü'nün birimleri ile ilişkilidir. Örneğin, iki ayrı elektrik yükü arasındaki kuvvet (klasik elektromanyetizma'nın vakumu) Coulomb Yasası tarafından verilmiştir:

${\displaystyle \ F_{\text{C}}={\frac {1}{4\pi \varepsilon _{0}}}{\frac {q_{1}q_{2}}{r^{2}}}}$

burada "q₁" ve "q₂" yükleri, r yüklerin arasındaki mesafeyi ifade eder. Aynı şekilde, Maxwell denklemlerinde görüldüğü gibi e0; elektrik alan, manyetik alan ve elektromanyetik radyasyondan bahseder ve bunların kendi kaynakları ile ilgilidir.

Değer

ε₀'ın değeri aşağıdaki formul ile belirlenir:${\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}}$ "C" klasik vakum içindeki ışık hızının SI cinsinden değeri  ve µ₀ ise Uluslararası Standartlar Kuruluşları'nın "manyetik sabit" (vakum geçirgenliği olarak da adlandırılır) olarak adlandırdığı parametre. µ₀  4π × 10⁻⁷H/m^-1  değerine sahip olduğundan ve C'nin değeri 299792458 m.s⁻¹olduğu için  e₀ 'ın değeri yaklaşık olarak,

ε₀ ≈ 8.8541878176208.854187817620... × 10^-12F⋅m⁻¹ (veya SI birimleri kullanılarak A²⋅s⁴⋅kg⁻¹⋅m^-3 , ya da SI birimlerinin dönüşümleri kullanılarak C²⋅N^-1⋅m^-2 şeklinde veya C⋅V^-1⋅m^-1 şeklinde yazılabilir).

Elektrik sabiti e₀'ı tarihsel kökeni ve değeri detaylı olarak aşağıda açıklanmıştır.

SI birimlerinin tanımlanması

Saniyedeki temel yük sabit sayısı (Amper) yeniden tanımlamak için öneriler kapsamında elektrik sabiti tam bir sabit değere sahip olacaktır. Elektron yükünün değeri tanımlanmış bir sabit olacak, ölçülmedi, ölçülmüş μ0 miktarında. Sonuç olarak, e₀ da kesin bir değere sahip değil. Daha önce olduğu gibi, bu denklem ε0 = 1 / (μ0c2) tarafından tanımlanan, ancak şimdi μ0, manyetik sabite ilişkin bir ölçüm hatası olacaktır. Bu ölçüm hatası ince yapı sabiti alfa ile ilişkili olabilir:

${\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}={\frac {e^{2}}{2\alpha hc}}\ ,}$

"e" birim yük, "h" Planck sabiti ve "c" vakum içindeki ışık hızı. Burada kullanımı yapılmış olan ilişkisi için ince yapı sabiti:

${\displaystyle \alpha ={\frac {\mu _{0}ce^{2}}{2h}}\ .}$

e₀  değerindeki belirsizlik nedeniyle ince yapı sabiti de aynı belirsizliğe sahip olabilir. Şu anda ise değeri 6990680000000000000 ah -6.8×10^-10.

Terminoloji

Tarihsel olarak, parametre e₀'ın bilinen birçok farklı ismi olmuştur. "vakum geçirgenlik" veya onun türevleri gibi "geçirgenlik/vakum" "boş uzayın geçirgenliği" veya "serbest uzayın geçirgenliği" gibi terimler yaygındır. Standart Organizasyonları dünya çapında bu miktar için tek tip bir terim olarak "elektrik sabiti" ismini kullanır ve resmi standartlar belgelerin de bu terim benimsenmiştir.

Bir diğer eş anlamı olan "dielektrik sabiti", mutlak geçirgenlik için geçmişte kullanıldığı gibi "vakum dielektrik sabiti" olarak da kullanıldı. Ancak, modern kullanımda "sabit dielektrik" tipik bir ε / ε0 münhasıran başvurur ve bu kullanım göreceli statik geçirgenlik lehine bazı standartlar organları tarafından "eski" olarak kabul edilir. Bu nedenle, elektrik sabit ε0 için "vakum dielektrik sabiti" terimi en modern yazarlar tarafından geçersiz kabul edilir, her ne kadar devam eden kullanımlarına zaman zaman denk gelinsede.

Harf gösterimi için, sabit olarak ya 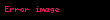${\displaystyle \varepsilon _{0}\,}$ ya da ${\displaystyle \epsilon _{0}\,}$ kullanılır. Ortak glifleri içinse harf olan epsilon kullanılır.

e0 parametresinin tarihçesi

Yukarıda belirtildiği gibi, parametre e₀ bir ölçüm sabitidir. Şimdi elektromanyetik miktarlarda tanımlamak için kullanılan denklemin varlığı, aşağıda tarif edilen  "rasyonalize" işleminin bir sonucudur. Ama bir değer tahsis yöntemi Maxwell denklemleri, boşlukta elektromanyetik dalgaların ışık hızı ile hareket ettiğini söylemektedir. ε0'ın neden böyle bir değere sahip olduğunun anlaşılması kısa tarihinin incelenmesini gerektirir.

Birimlerin rasyonalizasyonu

Coulomb ve diğer bilim insanlarının deneyleri gösterdi ki, iki eşit yük "elektriksel olarak eşit" arasındaki kuvvet "F", iki yük arasında yer alan mesafe "r" dışında bulunan boş alanda da olması gerekir. Bunun formülü;

${\displaystyle F=\;k_{\mathrm {e} }{\frac {Q^{2}}{r^{2}}},}$

burada "Q" iki yükün mevcut elektrik miktarını temsil eder ve "ke " Coulomb sabiti. Eğer hiçbir kısıtlama olmadan başlıyor ise, k_e değeri keyfi olarak seçilmiş olabilir.k_e 'nin her bir farklı seçimi için Q'nun farklı bir yorumlaması vardır, karışıklığı önlemek için, her bir farklı "yorumlama" için bir isim ve sembol tahsis edilmelidir.

19. yüzyılın sonlarında kararlaştırılan denklemler ve birimlerin sistemlerinden birinde, (cgs esu sistemi) "birimlerinin santimetre gram-saniye elektrostatik sistemi" olarak adlandırılan sistemde, ke sabiti 1'e eşit alınır ve  "Gauss elektrik yükü" qs ortaya çıkan denklem ile tanımlanır.

${\displaystyle F={\frac {{q_{\text{s}}}^{2}}{r^{2}}}.}$

Gauss yükünün birimi, statcoulomb, iki yükün 1 santimetre mesafede kuvvet CGS birimi dyn'a eşit bir kuvvetle birbirlerini itmesine eşittir. Böylece Gauss yükünü birimi de 1 dyne^1/2 cm şeklinde yazılabilir. "Gauss elektrik yükü" Modern (RMKS şöyle) ile aynı matematiksel miktar da elektrik yüküne sahip değildir ve Coulomb ile ölçülmez.

Bu fikir doğrultusunda, küresel geometri durumların da daha iyi olacağını, Coulomb kanunu gibi denklemlerin ise bir faktör "4π" içereceğini ve aşağıda gibi bir formda yazılması gerektiği fikri geliştirilmiştir.

${\displaystyle F=\;k'_{\mathrm {e} }{\frac {{q'_{\text{s}}}^{2}}{4\pi r^{2}}}.}$

Bu fikir "rasyonalizasyon" olarak adlandırılır.  q_s' ve k_e' miktar olarak aynı değil, tıpkı formülün önceki halinde olduğu gibi.  k_e'=1 olduğunda farklı büyüklükte bir elektrik birimini oluşturulur, ama yine de CGS ESU sistemi ile aynı boyutlara sahiptir.

Bir sonraki adım q sembolü ile gösterilen kendi başına temel yük miktarı olarak adlandırılan ve "elektrik miktarını" temsil eden miktarın belirlenmesi. Modern formda Coulomb Kanunu:

${\displaystyle \ F={\frac {1}{4\pi \varepsilon _{0}}}{\frac {q^{2}}{r^{2}}}.}$

Böylece rasyonalize metre kilogram-saniye (RMKS şöyle) denklem sisteminin veya "metre kilogram-saniye-amper (MKSA)" denklem sistemi olarak bilinen denklem sistemleri oluşturulmuştur. Bu sistemi tanımlamak için SI birimleri kullanılır. Yeni q miktarına "RMKS elektrik yükü" ya da günümüzde sadece "elektrik yükü" adı verilir. Açıkçası, eski cgs esu sisteminde kullanılan qs ile yeni q miktarı birbiriyle bağlantılıdır:

${\displaystyle \ q_{\text{s}}={\frac {q}{\sqrt {4\pi \varepsilon _{0}}}}.}$

e0 değerinin belirlenmesi

Kuvveti Newton biriminde, mesafeyi metre biriminde ve yükü mühendislerin pratik birimi Coulomb, 1 saniyede 1 amper aktığında biriken yük olarak tanımlanır, biriminde yazmayı gerektiren bir gereklilik olmuştur. Bunu gösteren parametre e₀ olmalıdır ve birimi C².N⁻¹.m⁻² (veya eşdeğer birimler ile pratik olarak "farad başına metre").

ε0 sayısal değerini oluşturmak amacıyla,Coulomb kanunu, ve diğer fikirlerin kullanılmasıyla Maxwell denklemleri geliştirilmiş, böylece yukarıdaki ε0, μ0 ve c0 arasında bir ilişkinin var olduğu belirtilmiştir. Prensip olarak, coulomb veya elektrik ve manyetizmanın temel birimi amperi yapmak için karar verirken bir seçim vardır. Dünya genelinde bu seçimde amper kullanılmıştır. Bu, yukarıda belirtildiği gibi ε0 değerinin C0 ve μ0 değerleri ile belirlendiği anlamına gelir.

Gerçek ortam geçirgenliği

Geleneksel olarak, elektrikli sabit ε0, elektrik değişim alanı D olarak tanımlanan değerler; elektrik alan E ve orta klasik elektrik polarizasyon yoğunluğu P ile bir ilişki içerisinde görünür. Genel olarak bu ilişki aşağıdaki formdadır:

${\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} .}$

Lineer dielektrik için P'nin E'ye dik olduğunu kabul ediyoruz, ancak gecikmiş bir izin ve mekansal olmayan yerel müdahale yüzünden en genel anlamda:

${\displaystyle \mathbf {D} (\mathbf {r} ,\ t)=\int _{-\infty }^{t}dt'\int d^{3}\mathbf {r} '\ \varepsilon (\mathbf {r} ,\ t;\mathbf {r} ',\ t')\mathbf {E} (\mathbf {r} ',\ t').}$

Bu durumunda yerbilmezlik ve cevabın gecikmesi önemli değildir. Bunun sonucunda:

${\displaystyle \mathbf {D} =\varepsilon \mathbf {E} =\varepsilon _{\text{r}}\varepsilon _{0}\mathbf {E} }$

Bu denklem de "e" geçirgenlik ve "er" bağıl yalıtkanlık sabiti. Klasik elektromanyetizmanın vacumunda, kutuplaşma P = 0, bu yüzden er = 1 ve e = e0 dır.

Ayrıca bakınız

• Casimir etkisi
• Bağıl geçirgenlik
• Coulomb Yasası
• Elektromanyetik dalga denklemi
• ISO 31-5
• Elektromanyetik alanın matematiksel açıklamaları
• Elektromanyetik dalga denkleminin sinüzoidal düzlem dalga çözümleri
• Dalga empedansı

Notlar

1. ^ electric constant"Electropedia: International Electrotechnical Vocabulary (IEC 60050)". Cenevre: International Electrotechnical Commission. 30 Haziran 2016 tarihinde kaynağından . Erişim tarihi: 26 Mart 2015. 
2. ^ The exact numerical value is found at: . NIST reference on constants, units, and uncertainty: Fundamental physical constants. NIST. 3 Haziran 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ocak 2012. 
3. ^ Quote from NIST: "The symbol c is the conventional symbol for the speed of light in vacuum.
4. ^ See the last sentence of the NIST definition of ampere 25 Nisan 2017 tarihinde Wayback Machine sitesinde ..
5. ^ See the last sentence of the NIST definition of meter 22 Mayıs 2018 tarihinde Wayback Machine sitesinde ..
6. ^ ^{a b c} Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008).
7. ^ A summary of the definitions of c, μ₀ and ε₀ is provided in the 2006 CODATA Report: CODATA report, pp. 6–7 12 Haziran 2018 tarihinde Wayback Machine sitesinde .
8. ^ Resolution 1 of 24th meeting of the General Conference on Weights and Measures (PDF). Sèvres, France: International Bureau for Weights and Measures. 21 Ekim 2011. 13 Ocak 2012 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 13 Haziran 2016. 
9. ^ SM Sze & Ng KK (2007). "Appendix E". Physics of semiconductor devices (Third bas.). New York: Wiley-Interscience. s. 788. ISBN . 31 Ağustos 2009 tarihinde kaynağından . Erişim tarihi: 13 Haziran 2016. 
10. ^ RS Muller, Kamins TI & Chan M (2003). Device electronics for integrated circuits (Third bas.). New York: Wiley. Inside front cover. ISBN . 31 Ağustos 2009 tarihinde kaynağından . Erişim tarihi: 13 Haziran 2016. 
11. ^ FW Sears, Zemansky MW & Young HD (1985). College physics. Reading, Mass.: Addison-Wesley. s. 40. ISBN . 
12. ^ B. E. A. Saleh and M. C. Teich, Fundamentals of Photonics (Wiley, 1991)
13. ^ International Bureau of Weights and Measures (2006). (PDF). s. 12. 3 Haziran 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 13 Haziran 2016. 
14. ^ ^{a b} Braslavsky, S.E. (2007). "Glossary of terms used in photochemistry (IUPAC recommendations 2006)" (PDF). Pure and Applied Chemistry. 79 (3). ss. 293-465; see p. 348. doi:10.1351/pac200779030293. 5 Temmuz 2016 tarihinde kaynağından (PDF). Erişim tarihi: 13 Haziran 2016. 
15. ^ "Naturkonstanten". Freie Universität Berlin. 1 Temmuz 2016 tarihinde kaynağından . Erişim tarihi: 13 Haziran 2016. 
16. ^ ^{a b} IEEE Standards Board (1997). "IEEE Standard Definitions of Terms for Radio Wave Propagation" (PDF). s. 6. 27 Haziran 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Haziran 2016. 
17. ^ For an introduction to the subject of choices for independent units, see John David Jackson (1999). "Appendix on units and dimensions". Classical electrodynamics (Third bas.). New York: Wiley. ss. 775 et seq.. ISBN . 4 Ağustos 2009 tarihinde kaynağından . Erişim tarihi: 13 Haziran 2016. 
18. ^ International Bureau of Weights and Measures. . 26 Mart 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Haziran 2016. 
19. ^ ε_r = 1