Büyük sayılar yasası

Büyük Sayılar Kanunu ya da Büyük Sayılar Yasası, bir rassal değişkenin uzun vadeli kararlılığını tanımlayan bir olasılık teoremidir. Sonlu bir beklenen değere sahip birbirinden bağımsız ve eşit dağılıma sahip bir rassal değişkenler örneklemi verildiğinde, bu gözlemlerin ortalaması sonuçta bu beklenen değere yakınsayacak ve bu değere yakın bir seyir izleyecektir.

Büyük Sayılar Kanunu bir zarın peş peşe atılması ile örneklenebilir. Öyle ki, multinom dağılımı sonucunda 1, 2, 3, 4, 5 ve 6 sayılarının gelme olasılığı eşittir. Bu sonuçların aritmetik ortalaması (ya da "beklenen değeri"),

(1+2+3+4+5+6)/6=3,5 olur.

Sağdaki grafik bir zarın atılması deneyinin sonuçlarını göstermektedir. Bu deneyde görürüz ki, ilk başta zar atışlarının ortalaması fazlaca dalgalanmaktadır. Büyük sayılar yasası tarafından öngörüldüğü üzere, gözlem sayısı arttıkça, ortalama, beklenen değerin yani 3,5'in etrafında dengelenmektedir.

Bir başka örnek madeni para atılması olabilir. Bir madeni paranın peş peşe atılması durumunda, yazıların (ya da turaların) sıklığı, gözlem sayısı arttıkça, %50'ye gittikçe yaklaşacaktır. Fakat yazı ve tura sayıları arasındaki mutlak fark atış sayısı arttıkça açılacaktır. Örneğin, 1000 atıştan sonra 520 ve 10000 atıştan sonra 5096 yazı görebiliriz. Ortalama,%52'den %50,96'ya gittiği, gerçek %50'ye yaklaştığı halde, ortalamadan toplam fark 40'tan 192'ye yükselmiştir.

Büyük Sayılar Kanunu önemlidir, çünkü rastgele olaylardan kararlı uzun-vadeli sonuçlar alınacağını "garanti eder". Örneğin, bir gazino tek bir Amerikan Rulet dönüşünden para kaybedebilir, ama 1000'lerce dönüşe oynanan paranın tamamının %5,3'üne yakınını neredeyse kesin olarak kazanacaktır. Bir oyuncunun herhangi bir kazancı, sonuçta oyunun başlıca parametreleri tarafından soğurulacaktır. Büyük sayılar yasasının büyük sayıda gözlem yapıldığı zaman etkili olacağı unutulmamalıdır. Küçük miktardaki gözlem için sonucun beklenen değere yaklaşacağını veya bir sapmanın hemen bir başkasıyla "dengeleneceğini" beklemek için bir neden yoktur. Kumarbaz aldanmasına bakabilirsiniz.

Geçmiş

Büyük Sayılar Kanunu ilk olarak Jacob Bernoulli tarafından tanımlanmıştır. 1713'te (Varsayımın Sanatı) adlı eserinde yayınlanan yeterli derecede titiz bir kanıtı geliştirebilmesi 20 yılına mal olmuştur. Bunu kendisinin "Altın Teoremi" olarak adlandırmış, fakat yaygın olarak "Bernoulli'nin Kuramı" olarak bilinmektedir ( fizik kuramıyla karıştırılmaması gerekir). 1835'te S.D. Poisson, bu yasayı "La loi des grands nombres" (Büyük sayılar yasası) olarak adlandırmıştır. İki isimde de anılagelen bu yasa için "Büyük sayılar yasası" terimi daha fazla kullanılmaktadır.

Bernoulli ve Poisson kendi çalışmalarını yayımladıktan sonra, Chebyshev, Markov, Borel, Cantelli ve Kolmogorov'un da aralarında yer aldığı diğer matematikçiler de yasanın gelişmesine katkıda bulunmuşlardır. Bu çalışmalar yasanın iki belirgin biçiminin ortaya konulmasında etkili olmuştur. Bu biçimlerden biri "zayıf" yasa, diğeri de "güçlü" yasa olarak adlandırılır. Bu biçimler farklı yasaları tanımlamamaktadır, sadece ölçülmüş olasılığın, gerçek olasılığa yakınsamasını tanımlamanın farklı yollarıdır ve büyük olan küçüğü içerir.

İspatı

X₁, X₂, ... şeklinde, E(X₁) = E(X₂) = ... = µ < ∞ biçiminde ifade edilebilecek sonlu bir beklenen değere sahip, sonsuz sayıda (bağımsız ve özdeş dağılmış rastgele değişken) rastgele değişken serisi verildiğinde, örneklemin ortalamasının yakınsadığı değeri arıyoruz:

${\displaystyle {\overline {X}}_{n}={\tfrac {1}{n}}(X_{1}+\cdots +X_{n}).}$

Büyük sayılar yasası - Zayıf yasa

Teorem: ${\displaystyle {\overline {X}}_{n}\,{\xrightarrow {P}}\,\mu \qquad {\textrm {for}}\qquad n\to \infty .}$

Chebyshev'in eşitsizliğini kullanarak kanıtı

Bu kanıt veryansın sonlu olduğu varsayımına dayanır: ${\displaystyle \operatorname {Var} (X_{i})=\sigma ^{2}}$ (tüm${\displaystyle i}$ değerleri için). Rastgele değişkenlerin bağımsız olması, aralarında herhangi bir korelasyon olmadığını belirtir ve ayrıca

${\displaystyle \operatorname {Var} ({\overline {X}}_{n})={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}.}$

Serinin genel ortalaması μ, örneklemin ortalamasıdır:

${\displaystyle E({\overline {X}}_{n})=\mu .}$

${\displaystyle {\overline {X}}_{n}}$ üzerinde kullanarak

${\displaystyle \operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|\geq \varepsilon )\leq {\frac {\sigma ^{2}}{n\varepsilon ^{2}}}.}$

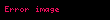
elde edilebilir. Bu, aşağıdakini elde etmek için kullanılabilir:

${\displaystyle \operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|<\varepsilon )=1-\operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|\geq \varepsilon )\geq 1-{\frac {\sigma ^{2}}{n\varepsilon ^{2}}}.}$

n sonsuza gittikçe, ifadenin değeri 1'e yaklaşır. Olasılıktaki yakınsama tanımı (bkz. ) gereği,

${\displaystyle {\overline {X}}_{n}\,{\xrightarrow {P}}\,\mu \qquad {\textrm {for}}\qquad n\to \infty .}$

sonucunu elde ederiz.

Karakteristik fonksiyonların yakınsamasını kullanarak kanıtı

gereğince herhangi bir rastgele değişkenin , X, μ sonlu ortalamasıyla, aşağıdaki şekilde yazılabilir:

${\displaystyle \varphi _{X}(t)=1+it\mu +o(t),\quad t\rightarrow 0.}$

Tüm X₁, X₂, ... değişkenleri aynı karakteristik fonksiyona sahiptir, böylece bunu φ_X ile belirtebiliriz.

Karakteristik fonksiyonların basit özelliklerini kullanarak

${\displaystyle \varphi _{{\frac {1}{n}}X}(t)=\varphi _{X}({\tfrac {t}{n}})\quad {\textrm {and}}\quad \varphi _{X+Y}(t)=\varphi _{X}(t)\varphi _{Y}(t)\quad {\textrm {if\,}}X\,{\textrm {and}}\,Y\,{\textrm {are\,\,independent}}.}$

Bu kurallar, ${\displaystyle \scriptstyle {\overline {X}}_{n}}$'in φ_X: cinsinden karakteristik fonksiyonunu hesaplamak için kullanılabilir:

${\displaystyle \varphi _{{\overline {X}}_{n}}(t)=\left[\varphi _{X}\left({t \over n}\right)\right]^{n}=\left[1+i\mu {t \over n}+o\left({t \over n}\right)\right]^{n}\,\rightarrow \,e^{it\mu },\quad {\textrm {as}}\quad n\rightarrow \infty .}$

Limit e^itμ, sabit rastgele değişken μ'nün karakteristik fonksiyonudur ve gereğince, ${\displaystyle \scriptstyle {\overline {X}}_{n}}$ dağılımda μ değerine yakınsar:

${\displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathcal {D}}}\,\mu \qquad {\textrm {for}}\qquad n\to \infty .}$

μ, dağılımdaki μ'ye yakınsamanın ve olasılıktaki μ'ye yakınsamanın eşit olduğunu ifade eden bir sabittir. (Bkz. ) Bu da şu anlama gelir:

${\displaystyle {\overline {X}}_{n}\,{\xrightarrow {P}}\,\mu \qquad {\textrm {for}}\qquad n\to \infty .}$

Bu kanıt gerçekte şu anlama gelmektedir ki, olasılıkta örneklem ortalaması, var olduğu sürece, merkezdeki karakteristik fonksiyonun türevine yakınsar.

Biçimler

Yasanın her iki ifadesi de örneklem ortalamasının

${\displaystyle {\overline {X}}_{n}={\frac {1}{n}}(X_{1}+\cdots +X_{n})}$

beklenen değere yakınsadığını

${\displaystyle {\overline {X}}_{n}\,\to \,\mu \qquad {\textrm {for}}\qquad n\to \infty }$

ifade eder. Burada X₁, X₂, ... değerleri E(X₁)=E(X₂) = ... = µ < ∞ beklenen değerlerine sahip, bağımsız ve eş aralıklı () sonsuz rassal değişken sırasını simgeler.

Bir sonlu varyans Var(X₁) = Var(X₂) = ... = σ² < ∞ varsayımına ihtiyaç yoktur. Büyük veya sonsuz varyans yakınsamayı daha yavaş kılacaktır, fakat büyük sayılar yasası hala geçerlidir. Kanıtları daha kolay ve kısa tutmak için bu varsayım genellikle yapılır.

Güçlü ve zayıf ifadeler arasındaki fark, hangi tür yakınsamadan bahsettiğimizdir.

Zayıf Yasa

Büyük sayıların zayıf yasası belirtmektedir ki, örneklem ortalamasının beklenen değere doğru gerçekleşir

${\displaystyle {\overline {X}}_{n}\,{\xrightarrow {P}}\,\mu \qquad {\textrm {for}}\qquad n\to \infty .}$

Bu, herhangi bir pozitif ε sayısı için

${\displaystyle \lim _{n\rightarrow \infty }\operatorname {P} \left(\left|{\overline {X}}_{n}-\mu \right|<\varepsilon \right)=1.}$

()

Olasılıkta yakınsamayı yorumlarsak, zayıf yasa der ki, birçok gözlemin ortalaması giderek ne kadar küçük olduğuna bakılmaksızın, verilen herhangi bir sıfırdan farklı sınır dahilinde olmak üzere, ortalamaya yakın olacaktır.

Bu ifadeye zayıf yasa denir, çünkü olasılıkta yakınsama, rassal değişkenlerin zayıf yakınsamasıdır.

Zayıf büyük sayılar yasasının bir sonucu .

Güçlü Yasa

Büyük sayıların güçlü yasası der ki, örneklem ortalamasının beklenen değere doğru gerçekleşir.

${\displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathrm {a.s.} }}\,\mu \qquad {\textrm {for}}\qquad n\to \infty .}$

Bu demektir ki,

${\displaystyle \operatorname {P} \left(\lim _{n\rightarrow \infty }{\overline {X}}_{n}=\mu \right)=1,}$

Kanıt, zayıf yasadan daha karmaşıktır. Bu yasa bir rassal değişkenin beklenen değerini "art arda örneklemin uzun-vadeli ortalaması" olan sezgisel yorumunu doğrular.

Bu ifade güçlü yasa olarak adlandırılmıştır, çünkü yakınsama, rassal değişkenlerin güçlü yakınsamasıdır. Güçlü yasa, zayıfı kapsar.

Büyük sayıların güçlü yasası, 'in özel durumu olarak görülebilir.

Etkinlikler ve gösteriler

Kuramı ve büyük sayılar yasasının uygulamalarını interaktif araçlarla görselleştiren çeşitli uygulamalar mevcuttur. adlı hands-on learning activity15 Mart 2020 tarihinde Wayback Machine sitesinde . kaynak ile beraber Java applet (select the Coin Toss LLN Experiment)28 Aralık 2014 tarihinde Wayback Machine sitesinde . sitesinde yer alan örnekler büyük sayılar yasasını güzel bir şekilde ifade eder.

Ayrıca bakınız

• Merkezi limit teoremi

Kaynakça

1. ^ Tijms, Henk (2007). Understanding Probability: Chance Rules in Everyday Life. Cambridge University Press. s. 17. ISBN . 
2. ^ Jakob Bernoulli, Ars Conjectandi: Usum & Applicationem Praecedentis Doctrinae in Civilibus, Moralibus & Oeconomicis, 1713, Chapter 4,(Translated into English by Oscar Sheynin)
3. ^ Hacking, Ian. (1983) "19th-century Cracks in the Concept of Determinism"

• Grimmett, G. R.; Stirzaker, D. R. (1992). Probability and Random Processes, 2nd Edition. Clarendon Press, Oxford. . 
• Durrett, Richard (1995). Probability: Theory and Examples, 2nd Edition. Duxbury Press. 
• Jacobsen, Martin (1992). Videregående Sandsynlighedsregning (Advanced Probability Theory) 3rd Edition. HCØ-tryk, Copenhagen. . 

Dış bağlantılar

• [1] 4 Eylül 2021 tarihinde Wayback Machine sitesinde . MathWorld: Zayıf büyük sayılar yasası.
• [2] 23 Eylül 2008 tarihinde Wayback Machine sitesinde . MathWorld: Güçlü büyük sayılar yasası.
• Şans tabloları yasası - rastgele şansa bağlanabilenden daha büyük olduğu iddia edilen başarıların sınanması için kullanılır.