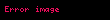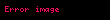Matematikte, Wallis çarpımı, sayısını olarak veren bir ifadedir. 1656'da tarafından yayınlanmıstır ve şu şekilde ifade edilmektedir:
İntegral yoluyla kanıt
Wallis bu sonsuz çarpımı enterpolasyon kullanarak türetmiştir; ancak, yöntemi titiz olarak kabul edilmemektedir. Daha modern bir çıkarım, 
bir hali olan
tanımlayalım. Kısmi integral yöntemi kullanarak
Şimdi, kolaylık olması açısından iki değişken ikâmesi yaparak şunu elde edelim:


Çift değerler için hesaplamak için 

Tek değerler için de benzer bir yöntem takip edilebilir ve 
Ayrıca, 
olduğunu gözlemliyoruz. Her iki tarafı 


elde ediyoruz. Sıkıştırma teoremi ile
elde edilir. Yani,
elde edilir.
Sinüs fonksiyonu için Euler'in sonsuz çarpımını kullanarak kanıt
Yukarıdaki ispat genellikle modern kalkülüs ders kitaplarında yer alsa da, geriye dönüp bakıldığında Wallis çarpımı, sinüs fonksiyonu için daha sonra elde edilmişl olan Euler sonsuz çarpımının kolay bir sonucu olarak ortaya çıkar.

Stirling yaklaşımıyla ilişkisi
Faktöriyel fonksiyonu 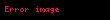
Wallis çarpımındaki sonlu çarpımları ele elalım:
Bu çarpımları yeniden düzenleyerek
yazabiliriz. Bu ifadede Stirling yaklaşımını hem 



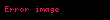
Riemann zeta fonksiyonunun sıfır noktasında türevi
Riemann zeta fonksiyonu ve Dirichlet eta fonksiyonu şu şekilde tanımlanabilir:
Son seriye Euler dönüşümü uygulandığında aşağıdaki elde edilir:
Ayrıca bakınız
Kaynaklar
Dş bağlantılar
- Hazewinkel, Michiel, (Ed.) (2001), "Wallis formula", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN
- "Why does this product equal π/2? A new proof of the Wallis formula for π". 3Blue1Brown. 20 Nisan 2018. 12 Aralık 2021 tarihinde kaynağından arşivlendi – YouTube vasıtasıyla.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Wallis carpimi p displaystyle pi sayisini olarak veren bir ifadedir 1656 da tarafindan yayinlanmistir ve su sekilde ifade edilmektedir p2 n 1 4n24n2 1 n 1 2n2n 1 2n2n 1 21 23 43 45 65 67 87 89 displaystyle begin aligned frac pi 2 amp prod n 1 infty frac 4n 2 4n 2 1 prod n 1 infty left frac 2n 2n 1 cdot frac 2n 2n 1 right 6pt amp Big frac 2 1 cdot frac 2 3 Big cdot Big frac 4 3 cdot frac 4 5 Big cdot Big frac 6 5 cdot frac 6 7 Big cdot Big frac 8 7 cdot frac 8 9 Big cdot cdots end aligned Integral yoluyla kanitWallis bu sonsuz carpimi enterpolasyon kullanarak turetmistir ancak yontemi titiz olarak kabul edilmemektedir Daha modern bir cikarim 0psinn xdx displaystyle int 0 pi sin n x dx integrali n tek ve cift degerler alirken incelenerek elde edilebilir bir hali olan I n 0psinn xdx displaystyle I n int 0 pi sin n x dx tanimlayalim Kismi integral yontemi kullanarak u sinn 1 x du n 1 sinn 2 xcos xdxdv sin xdx v cos x displaystyle begin aligned u amp sin n 1 x Rightarrow du amp n 1 sin n 2 x cos x dx dv amp sin x dx Rightarrow v amp cos x end aligned I n 0psinn xdx sinn 1 xcos x 0p 0p cos x n 1 sinn 2 xcos xdx 0 n 1 0pcos2 xsinn 2 xdx n gt 1 n 1 0p 1 sin2 x sinn 2 xdx n 1 0psinn 2 xdx n 1 0psinn xdx n 1 I n 2 n 1 I n n 1nI n 2 I n I n 2 n 1n displaystyle begin aligned Rightarrow I n amp int 0 pi sin n x dx 6pt amp sin n 1 x cos x Biggl 0 pi int 0 pi cos x n 1 sin n 2 x cos x dx 6pt amp 0 n 1 int 0 pi cos 2 x sin n 2 x dx qquad n gt 1 6pt amp n 1 int 0 pi 1 sin 2 x sin n 2 x dx 6pt amp n 1 int 0 pi sin n 2 x dx n 1 int 0 pi sin n x dx 6pt amp n 1 I n 2 n 1 I n 6pt amp frac n 1 n I n 2 6pt Rightarrow frac I n I n 2 amp frac n 1 n 6pt end aligned Simdi kolaylik olmasi acisindan iki degisken ikamesi yaparak sunu elde edelim I 2n 2n 12nI 2n 2 displaystyle I 2n frac 2n 1 2n I 2n 2 I 2n 1 2n2n 1I 2n 1 displaystyle I 2n 1 frac 2n 2n 1 I 2n 1 I 0 displaystyle I 0 ve I 1 displaystyle I 1 degerleri sonradan kullanmak uzere hemen ve kolaylikla hesapalanabilir I 0 0pdx x 0p pI 1 0psin xdx cos x 0p cos p cos 0 1 1 2 displaystyle begin aligned I 0 amp int 0 pi dx x Biggl 0 pi pi 6pt I 1 amp int 0 pi sin x dx cos x Biggl 0 pi cos pi cos 0 1 1 2 6pt end aligned Cift degerler icin hesaplamak icin I 2n displaystyle I 2n baglantisini tekrarlayarak kullaniyoruz ve daha once hesaplanan I 0 displaystyle I 0 degerinde duruyoruz I 2n 0psin2n xdx 2n 12nI 2n 2 2n 12n 2n 32n 2I 2n 4 displaystyle I 2n int 0 pi sin 2n x dx frac 2n 1 2n I 2n 2 frac 2n 1 2n cdot frac 2n 3 2n 2 I 2n 4 2n 12n 2n 32n 2 2n 52n 4 56 34 12I 0 p k 1n2k 12k displaystyle frac 2n 1 2n cdot frac 2n 3 2n 2 cdot frac 2n 5 2n 4 cdot cdots cdot frac 5 6 cdot frac 3 4 cdot frac 1 2 I 0 pi prod k 1 n frac 2k 1 2k Tek degerler icin de benzer bir yontem takip edilebilir ve I 1 displaystyle I 1 degerinde durulur I 2n 1 0psin2n 1 xdx 2n2n 1I 2n 1 2n2n 1 2n 22n 1I 2n 3 displaystyle I 2n 1 int 0 pi sin 2n 1 x dx frac 2n 2n 1 I 2n 1 frac 2n 2n 1 cdot frac 2n 2 2n 1 I 2n 3 2n2n 1 2n 22n 1 2n 42n 3 67 45 23I 1 2 k 1n2k2k 1 displaystyle frac 2n 2n 1 cdot frac 2n 2 2n 1 cdot frac 2n 4 2n 3 cdot cdots cdot frac 6 7 cdot frac 4 5 cdot frac 2 3 I 1 2 prod k 1 n frac 2k 2k 1 Ayrica sin x x displaystyle sin x leq x gercegine dayanarak sin2n 1 x sin2n x sin2n 1 x 0 x p displaystyle sin 2n 1 x leq sin 2n x leq sin 2n 1 x 0 leq x leq pi I 2n 1 I 2n I 2n 1 displaystyle Rightarrow I 2n 1 leq I 2n leq I 2n 1 oldugunu gozlemliyoruz Her iki tarafi I 2n 1 displaystyle I 2n 1 ile bolerek ve ayrica I 2n 2n 12nI 2n 2 displaystyle I 2n frac 2n 1 2n I 2n 2 ve I 2n 1 2n2n 1I 2n 1 displaystyle I 2n 1 frac 2n 2n 1 I 2n 1 baglantilarini kullanarak 1 I 2n I 2n 1 I 2n 1 I 2n 1 2n 12n displaystyle Rightarrow 1 leq frac I 2n I 2n 1 leq frac I 2n 1 I 2n 1 frac 2n 1 2n elde ediyoruz Sikistirma teoremi ile limn I 2n I 2n 1 1 displaystyle Rightarrow lim n rightarrow infty frac I 2n I 2n 1 1 elde edilir Yani limn I 2n I 2n 1 p2limn k 1n 2k 12k 2k 12k 1 displaystyle lim n rightarrow infty frac I 2n I 2n 1 frac pi 2 lim n rightarrow infty prod k 1 n left frac 2k 1 2k cdot frac 2k 1 2k right 1 p2 k 1 2k2k 1 2k2k 1 21 23 43 45 65 67 displaystyle Rightarrow frac pi 2 prod k 1 infty left frac 2k 2k 1 cdot frac 2k 2k 1 right frac 2 1 cdot frac 2 3 cdot frac 4 3 cdot frac 4 5 cdot frac 6 5 cdot frac 6 7 cdot cdots elde edilir Sinus fonksiyonu icin Euler in sonsuz carpimini kullanarak kanitYukaridaki ispat genellikle modern kalkulus ders kitaplarinda yer alsa da geriye donup bakildiginda Wallis carpimi sinus fonksiyonu icin daha sonra elde edilmisl olan Euler sonsuz carpiminin kolay bir sonucu olarak ortaya cikar sin xx n 1 1 x2n2p2 displaystyle frac sin x x prod n 1 infty left 1 frac x 2 n 2 pi 2 right x p2 displaystyle x frac pi 2 olsun O zaman 2p n 1 1 14n2 p2 n 1 4n24n2 1 n 1 2n2n 1 2n2n 1 21 23 43 45 65 67 displaystyle begin aligned Rightarrow frac 2 pi amp prod n 1 infty left 1 frac 1 4n 2 right 6pt Rightarrow frac pi 2 amp prod n 1 infty left frac 4n 2 4n 2 1 right 6pt amp prod n 1 infty left frac 2n 2n 1 cdot frac 2n 2n 1 right frac 2 1 cdot frac 2 3 cdot frac 4 3 cdot frac 4 5 cdot frac 6 5 cdot frac 6 7 cdots end aligned Stirling yaklasimiyla iliskisiFaktoriyel fonksiyonu n displaystyle n icin ifade edilen Stirling yaklasimi sunu ifade eder n 2pn ne n 1 O 1n displaystyle n sqrt 2 pi n left frac n e right n left 1 O left frac 1 n right right Wallis carpimindaki sonlu carpimlari ele elalim pk n 1k2n2n 12n2n 1 displaystyle p k prod n 1 k frac 2n 2n 1 frac 2n 2n 1 Bu carpimlari yeniden duzenleyerek pk 12k 1 n 1k 2n 4 2n 2n 1 2 12k 1 24k k 4 2k 2 displaystyle begin aligned p k amp 1 over 2k 1 prod n 1 k frac 2n 4 2n 2n 1 2 6pt amp 1 over 2k 1 cdot 2 4k k 4 over 2k 2 end aligned yazabiliriz Bu ifadede Stirling yaklasimini hem k displaystyle k hem de 2k displaystyle 2k icin kullanirsak pk displaystyle p k nin k displaystyle k rightarrow infty iken p2 displaystyle frac pi 2 ifadesine yakinsadigi gosterilebilir Riemann zeta fonksiyonunun sifir noktasinda tureviRiemann zeta fonksiyonu ve Dirichlet eta fonksiyonu su sekilde tanimlanabilir z s n 1 1ns ℜ s gt 1h s 1 21 s z s n 1 1 n 1ns ℜ s gt 0 displaystyle begin aligned zeta s amp sum n 1 infty frac 1 n s Re s gt 1 6pt eta s amp 1 2 1 s zeta s 6pt amp sum n 1 infty frac 1 n 1 n s Re s gt 0 end aligned Son seriye Euler donusumu uygulandiginda asagidaki elde edilir h s 12 12 n 1 1 n 1 1ns 1 n 1 s ℜ s gt 1 h s 1 21 s z s 21 s ln 2 z s 12 n 1 1 n 1 ln nns ln n 1 n 1 s ℜ s gt 1 displaystyle begin aligned eta s amp frac 1 2 frac 1 2 sum n 1 infty 1 n 1 left frac 1 n s frac 1 n 1 s right Re s gt 1 6pt Rightarrow eta s amp 1 2 1 s zeta s 2 1 s ln 2 zeta s 6pt amp frac 1 2 sum n 1 infty 1 n 1 left frac ln n n s frac ln n 1 n 1 s right Re s gt 1 end aligned h 0 z 0 ln 2 12 n 1 1 n 1 ln n ln n 1 12 n 1 1 n 1ln nn 1 12 ln 12 ln 23 ln 34 ln 45 ln 56 12 ln 21 ln 23 ln 43 ln 45 ln 65 12ln 21 23 43 45 12ln p2 z 0 12ln 2p displaystyle begin aligned Rightarrow eta 0 amp zeta 0 ln 2 frac 1 2 sum n 1 infty 1 n 1 left ln n ln n 1 right 6pt amp frac 1 2 sum n 1 infty 1 n 1 ln frac n n 1 6pt amp frac 1 2 left ln frac 1 2 ln frac 2 3 ln frac 3 4 ln frac 4 5 ln frac 5 6 cdots right 6pt amp frac 1 2 left ln frac 2 1 ln frac 2 3 ln frac 4 3 ln frac 4 5 ln frac 6 5 cdots right 6pt amp frac 1 2 ln left frac 2 1 cdot frac 2 3 cdot frac 4 3 cdot frac 4 5 cdot cdots right frac 1 2 ln frac pi 2 Rightarrow zeta 0 amp frac 1 2 ln left 2 pi right end aligned Ayrica bakinizKaynaklar a b c Wallis Formula Arsivlenmesi gereken baglantiya sahip kaynak sablonu iceren maddeler link Ds baglantilarHazewinkel Michiel Ed 2001 Wallis formula Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Why does this product equal p 2 A new proof of the Wallis formula for p 3Blue1Brown 20 Nisan 2018 12 Aralik 2021 tarihinde kaynagindan arsivlendi YouTube vasitasiyla
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

![{\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\prod _{n=1}^{\infty }{\frac {4n^{2}}{4n^{2}-1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)\\[6pt]&={\Big (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\Big )}\cdot {\Big (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\Big )}\cdot {\Big (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\Big )}\cdot {\Big (}{\frac {8}{7}}\cdot {\frac {8}{9}}{\Big )}\cdot \;\cdots \\\end{aligned}}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5a1pqVTVZbVk0WVdFMk4ySTJaR1ptT0dKbE5tTm1abUkwWmpVNU56YzNZMlZoT0RJNE5EVTAuc3Zn.svg)