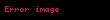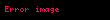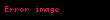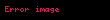Yassılaşma veya düzleşme sırasıyla bir elips veya bir elipsoid (sferoid) şeklini almak üzere bir dairenin veya kürenin bir çap boyunca sıkışmasının bir ölçüsüdür. Kullanılan diğer terimler eliptiklik veya oblatlıktır (basıklık). Düzleştirme için olağan gösterim 'dir ve elde edilen elips veya elipsoidin ve yarı eksenleri cinsinden tanımı şöyledir:


Sıkıştırma faktörü 'dır Her durumda; elips için bu aynı zamanda en boy oranını ifade eder.
Tanımlar
Bazen birinci düzleştirme olarak adlandırılan 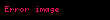
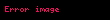
Aşağıda, 𝑎 daha büyük boyuttur (örneğin yarı büyük eksen), oysa 𝑏 daha küçüktür ( yarı küçük eksen). Bir daire için tüm düzleştirmeler sıfırdır (a = b).
(Birinci) yassılaşma Temel. Jeodezik referans elipsoidler verilerek belirtilir.
İkincil yassılaşma Nadiren kullanılır. Üçüncül yassılaşma Jeodezik hesaplamalarda küçük bir genişleme parametresi olarak kullanılır.
Kimlikler
Düzleşmeler birbiriyle ilişkili olabilir:
Düzleşmeler elipsin diğer parametreleriyle de ilgilidir. Örneğin,
bu formülde 
Ayrıca bakınız
Kaynakça
- ^ Snyder, John P. (1987). Map Projections: A Working Manual. U.S. Geological Survey Professional Paper. 1395. Washington, D.C.: U.S. Government Printing Office. doi:10.3133/pp1395. 17 Mayıs 2011 tarihinde kaynağından .
- ^ Tenzer, Róbert (2002). "Transformation of the Geodetic Horizontal Control to Another Reference Ellipsoid". Studia Geophysica et Geodaetica. 46 (1). ss. 27-32. doi:10.1023/A:1019881431482. 750849329. 15 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 28 Haziran 2024.
- ^ Maling, Derek Hylton (1992). Coordinate Systems and Map Projections. 2nd. Oxford; New York: Pergamon Press. s. 65. ISBN .
- ^ For example,
is called the second flattening in: Taff, Laurence G. (1980). An Astronomical Glossary. MIT Lincoln Lab. s. 84. 10 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 28 Haziran 2024.
- ^ Lapaine, Miljenko (2017). "Basics of Geodesy for Map Projections". Usery, E. Lynn (Ed.). Choosing a Map Projection. Lecture Notes in Geoinformation and Cartography. ss. 327-343. doi:10.1007/978-3-319-51835-0_13. ISBN . r eksik
|soyadı1=() - ^ F. W. Bessel, 1825, Uber die Berechnung der geographischen Langen und Breiten aus geodatischen Vermessungen, Astron.Nachr., 4(86), 241–254, DOI:10.1002/asna.201011352, translated into English by C. F. F. Karney and R. E. Deakin as The calculation of longitude and latitude from geodesic measurements, Astron. Nachr. 331(8), 852–861 (2010), E-print arXiv:0908.1824, Bibcode: 1825AN......4..241B
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Yassilasma veya duzlesme sirasiyla bir elips veya bir elipsoid sferoid seklini almak uzere bir dairenin veya kurenin bir cap boyunca sikismasinin bir olcusudur Kullanilan diger terimler eliptiklik veya oblatliktir basiklik Duzlestirme icin olagan gosterim f displaystyle f dir ve elde edilen elips veya elipsoidin a displaystyle a ve b displaystyle b yari eksenleri cinsinden tanimi soyledir Elips seklinde a yaricapli bir daire Yaricapli bir kure yassi bir donus elipsoidine a f a ba displaystyle f frac a b a Sikistirma faktoru b a displaystyle b a dir Her durumda elips icin bu ayni zamanda en boy oranini ifade eder TanimlarBazen birinci duzlestirme olarak adlandirilan f displaystyle f duzlestirmesinin yani sira her biri bazen ikinci duzlestirme olarak da adlandirilan bazen sadece bir sembol olarak verilen veya bazen sirasiyla ikinci duzlestirme ve ucuncu duzlestirme olarak tanimlanan diger iki duzlestirmeler f displaystyle f ve n displaystyle n olmak uzere uc farkli degisken vardir Asagida 𝑎 daha buyuk boyuttur ornegin yari buyuk eksen oysa 𝑏 daha kucuktur yari kucuk eksen Bir daire icin tum duzlestirmeler sifirdir a b Birinci yassilasma f displaystyle f a ba displaystyle frac a b a Temel Jeodezik referans elipsoidler 1f displaystyle frac 1 f verilerek belirtilir Ikincil yassilasma f displaystyle f a bb displaystyle frac a b b Nadiren kullanilir Ucuncul yassilasma n displaystyle n a ba b displaystyle frac a b a b Jeodezik hesaplamalarda kucuk bir genisleme parametresi olarak kullanilir dd KimliklerDuzlesmeler birbiriyle iliskili olabilir f 2n1 n n f2 f displaystyle begin aligned f frac 2n 1 n 5mu n frac f 2 f end aligned Duzlesmeler elipsin diger parametreleriyle de ilgilidir Ornegin ba 1 f 1 n1 n e2 2f f2 4n 1 n 2 f 1 1 e2 displaystyle begin aligned frac b a amp 1 f frac 1 n 1 n 5mu e 2 amp 2f f 2 frac 4n 1 n 2 5mu f amp 1 sqrt 1 e 2 end aligned bu formulde e displaystyle e ile gosterilen deger eksantrikliktir Ayrica bakinizEksantriklik matematik Kaynakca Snyder John P 1987 Map Projections A Working Manual U S Geological Survey Professional Paper 1395 Washington D C U S Government Printing Office doi 10 3133 pp1395 17 Mayis 2011 tarihinde kaynagindan Tenzer Robert 2002 Transformation of the Geodetic Horizontal Control to Another Reference Ellipsoid Studia Geophysica et Geodaetica 46 1 ss 27 32 doi 10 1023 A 1019881431482 750849329 15 Nisan 2023 tarihinde kaynagindan Erisim tarihi 28 Haziran 2024 Maling Derek Hylton 1992 Coordinate Systems and Map Projections 2nd Oxford New York Pergamon Press s 65 ISBN 0 08 037233 3 For example f displaystyle f is called the second flattening in Taff Laurence G 1980 An Astronomical Glossary MIT Lincoln Lab s 84 10 Nisan 2023 tarihinde kaynagindan Erisim tarihi 28 Haziran 2024 Lapaine Miljenko 2017 Basics of Geodesy for Map Projections Usery E Lynn Ed Choosing a Map Projection Lecture Notes in Geoinformation and Cartography ss 327 343 doi 10 1007 978 3 319 51835 0 13 ISBN 978 3 319 51834 3 r eksik soyadi1 yardim F W Bessel 1825 Uber die Berechnung der geographischen Langen und Breiten aus geodatischen Vermessungen Astron Nachr 4 86 241 254 DOI 10 1002 asna 201011352 translated into English by C F F Karney and R E Deakin as The calculation of longitude and latitude from geodesic measurements Astron Nachr 331 8 852 861 2010 E print arXiv 0908 1824 Bibcode 1825AN 4 241B
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State