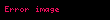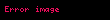| ||
| basık (oblate) | kutuplarda uzatılmış (prolate) | |
|---|---|---|
Bir sferoit, küremsi veya dönel elipsoit, bir elipsin ana eksenlerinden biri etrafında döndürülmesiyle elde edilen kuadrik bir yüzeydir; başka bir deyişle, iki eşit yarıçapa sahip bir elipsoitdir. Bir sferoit, sahiptir.
Elips, ana ekseni etrafında döndürülürse, sonuç, bir Amerikan futbolu veya ragbi topu biçiminde şekillendirilmiş, kutuplarda uzatılmış (prolate) bir sferoittir. Elips, küçük ekseni etrafında döndürülürse, sonuç mercimek şeklinde yassı (düzleştirilmiş, oblate) bir sferoittir. Cismi oluşturan elips bir daire ise, sonuç küredir.
Yerçekimi ve dönmenin birleşik etkileri nedeniyle, Dünya'nın şekli (ve tüm gezegenlerin) tam olarak bir küre değildir, bunun yerine dönüş ekseni yönünde hafifçe düzleştirilmiştir. Bu nedenle, haritacılık ve jeodezide Dünya'ya genellikle bir küre yerine referans elipsoid olarak bilinen basık bir sferoit olarak yaklaşılır. Mevcut Dünya Jeodezik Sistemi modeli, yarıçapı Ekvatorda 6,378137 km (3,963191 mi) ve kutuplarda 6,356752 km (3,949903 mi) olan bir sferoit kullanır.
Sferoid kelimesi, aslında iki veya üç eksenli elipsoidal şeklin ötesinde düzensizlikleri kabul eden "yaklaşık olarak küresel bir gövde" anlamına geliyordu ve bu terim, jeodezi hakkındaki bazı eski makalelerde (örneğin, Yeryüzünün kesik küresel harmonik genişlemelerine atıfta bulunarak) bu şekilde kullanılmaktadır.
Denklemi

Koordinat eksenleri boyunca hizalanmış a, b ve c yarı eksenleri ile orijinde merkezlenmiş üç eksenli bir elipsoidin denklemi
Bir sferoidin simetri ekseni olarak z alınırsa ve a = b olarak ayarlanırsa denklemi aşağıdaki şekilde verilir:
Yarı eksen a, sferoitin ekvator yarıçapıdır ve c, simetri ekseni boyunca merkezden kutba olan mesafedir. Olası iki durum vardır:
- c < a: kutuplardan basık (oblate) sferoit,
- c > a: kutuplara doğru uzatılmış (prolate) sferoit,
a = c durumu ise bir küreye indirgenir.
Özellikleri
Alan
c < a olan yassı bir sferoid aşağıdaki yüzey alanına sahiptir:
Yassı sferoit, yarı büyük ekseni a ve yarı küçük ekseni c olan bir elipsin z ekseni etrafında dönerek oluşturulur, bu nedenle e eksantriklik olarak tanımlanabilir. (Bkz. Elips)
c > a olan bir kutuplara doğru uzatılmış sferoit aşağıdaki yüzey alanına sahiptir:
Kutuplara doğru uzatılmış (prolate) sferoit, yarı büyük ekseni c ve yarı küçük ekseni a ile bir elipsin z ekseni etrafında dönerek oluşturulur; bu nedenle, e yine eksantriklik olarak tanımlanabilir. (Bkz. Elips)
Bu formüller Sbasık formülü aynı şekilde uzatılmış küremsi ve yardımcısı yüzey alanının hesaplanması için aynı şekilde kullanılabilir. Bununla birlikte, e daha sonra sanal hale gelir ve artık doğrudan eksantriklikle tanımlanamaz. Bu sonuçların her ikisi de, standart matematiksel özdeşlikler ve elipsin parametreleri arasındaki ilişkiler kullanılarak birçok başka biçime dönüştürülebilir.
Hacim
Bir küremsi içindeki hacim 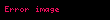
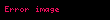
Eğrilik
Bir sferoit aşağıdaki şekilde parametrik olarak ifade edilmişse;
burada β, azaltılmış veya parametrik enlem, λ boylam, −π2 < β < +π2 ve −π < λ < +π olmak üzere, aşağıdaki şekilde hesaplanır;
ve ise aşağıdaki şekilde hesaplanır:
Bu eğriliklerin her ikisi de her zaman pozitiftir, böylece bir sfero üzerindeki her nokta eliptiktir.
En boy oranı
Bir yassı sferoidin/elipsin , c : a, kutupsal uzunlukların ekvatoryal uzunluklara oranıdır, (aynı zamanda basıklık olarak da adlandırılır) f, ekvator-kutup uzunluğu farkının ekvator uzunluğuna oranıdır:
İlk eksantriklik (genellikle yukarıdaki gibi basitçe eksantriklik) genellikle yassılaşma yerine kullanılır. Şu şekilde tanımlanır:
Eksantriklik ve basıklık arasındaki ilişkiler şunlardır:
,
Tüm modern jeodezik elipsoidler, yarı büyük eksen ile birlikte yarı küçük eksen (en-boy oranını verir), düzleştirme veya ilk eksantriklik ile tanımlanır. Bu tanımlar matematiksel olarak birbirinin yerine kullanılabilirken, gerçek dünyadaki hesaplamaların bir miktar kesinlik kaybetmesine neden olur. Karışıklığı önlemek için, elipsoidal bir tanım, kendi değerlerinin verdiği biçimde kesin olduğunu kabul eder.
Uygulamaları
Bir atom çekirdeğindeki protonların ve nötronların yoğunluk dağılımı için en yaygın şekiller küresel, uzatılmış ve basık sferoidaldir; burada kutup ekseninin dönme ekseni (veya dönme açısal momentum vektörünün yönü) olduğu varsayılır. Protonlar arasındaki elektromanyetik itme, yüzey gerilimi ve kuantum kabuk etkileri arasındaki rekabetin bir sonucu olarak deforme nükleer şekiller oluşur.
Basık sferoitler

Basık sferoit, Dünya, Satürn, Jüpiter ve hızla dönen yıldız Altair dahil olmak üzere, dönen gezegenlerin ve diğer gök cisimlerinin yaklaşık şeklidir. Satürn, 0.09796 ile Güneş Sistemindeki en uzatılmış gezegendir. 'in sarkaç deneylerinden ve Christiaan Huygens'in teorilerinden yola çıkan aydınlanma bilimcisi Isaac Newton, Jüpiter ve Dünya'nın merkezkaç kuvveti nedeniyle basık sferoidler olduğunu düşündü. Dünyanın çeşitli kartografik ve jeodezik sistemleri, tümü basık olan referans elipsoidlere dayanmaktadır.
Son derece uzatılmış bir gezegenin Bilimkurgu örneği, 'in romanından 'dir.
Uzatılmış sferoidler

Uzatılmış sferoid, ragbi futbolu gibi çeşitli spor dallarında topun yaklaşık şeklidir.
Aslında üç eksenli Elipsoitler olsalar da Güneş Sisteminin çeşitli uyduları yaklaşık uzatılmış sferoidler şeklindedir. Örnekler Satürn'ün uyduları Mimas, Enceladus ve Tethys ile Uranüs'ün uydusu Miranda'dır.
Gök cisimleri, yakın bir yörüngede devasa bir cismin yörüngesinde döndüklerinde, şekilleri hızlı dönme yoluyla baskın sferoitlere doğru bozulmanın aksine, gelgit kuvvetleri yoluyla hafifçe uzatılmış sferoitlere doğru bozulur. En uç örnek, Jüpiter'in uydusu Io'dur ve hafif bir eksantriklik nedeniyle yörüngesinde az çok uzatılarak yoğun volkanizmaya neden olur. Uzatılmış sferoitin ana ekseni bu durumda uydunun kutuplarından geçmez, ekvator üzerindeki iki noktadan doğrudan öncüle doğru ve uzağa bakan iki noktadan geçer.
Terim ayrıca Yengeç Bulutsusu gibi bazı bulutsuların şeklini tanımlamak için de kullanılır. Uzayda dalga yayılmasını ve girişimi analiz etmek için kullanılan , bir verici ile alıcı arasındaki doğrudan görüş hattı boyunca hizalanmış ana eksenlere sahip bir dizi eş merkezli uzatılmış sferoidlerdir.
Atom çekirdeklerinin ve aktinit ve lantanit elemanları uzatılmış sferoidler şeklinde biçimlendirilmiştir. Anatomide testis gibi sferoidlere yakın organlar (uzun ve kısa eksenleri) ile ölçülebilir.
Birçok denizaltı, uzatılmış sferoit olarak tanımlanabilecek bir şekle sahiptir.
Dinamik özellikler
Düzgün yoğunluğa sahip bir sferoit için, eylemsizlik momenti, ek bir simetri eksenine sahip bir elipsoidinkidir. Bir sferoitin ana ekseni c ve küçük eksenleri a ve b olarak tanımlandığında, bu ana eksenler boyunca eylemsizlik momentleri C, A ve B'dir. Bununla birlikte, bir sferoidde küçük eksenler simetriktir. Bu nedenle, ana eksenler boyunca eylemsizlik terimleri şunlardır:
burada M, cismin kütlesi olarak tanımlanır
Ayrıca bakınız
Kaynakça
- ^ . 8 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2020.
- ^ Torge, Wolfgang (2001). Geodesy (3. bas.). Berlin, New York: . s. 104. ISBN . OCLC 46641599.
- ^ Bu sonucun bir türevi şu adreste bulunabilir: . Mathworld.wolfram.com. 3 Eylül 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Haziran 2014.
- ^ Bu sonucun bir türevi şu adreste bulunabilir: . Mathworld.wolfram.com. 7 Ekim 2003. 21 Haziran 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Haziran 2014.
- ^ Brial, Pierre; Shaalan, Cécile (Kasım 2009), Introduction à la Géodésie et au Géopositionnement par satellites (PDF) (Fransızca), s. 8, doi:10.13140/RG.2.2.30646.86085, 30 Ekim 2020 tarihinde kaynağından (PDF), erişim tarihi: 29 Aralık 2020
- ^ Greenburg, John L. (1995). "Isaac Newton and the Problem of the Earth's Shape". History of Exact Sciences. Springer. 49 (4): 371-391. doi:10.1007/BF00374704. JSTOR 41134011.
- ^ Durant, Will; Durant, Ariel (28 Temmuz 1997). The Story of Civilization: The Age of Louis XIV. MJF Books. ISBN .
- ^ (Ekim 1973), "The Distance to the Crab Nebula and NP 0532", Publications of the Astronomical Society of the Pacific, 85 (507), s. 579, Bibcode:1973PASP...85..579T, doi:10.1086/129507
- ^ . Encyclopedia Britannica. 7 Eylül 2015 tarihinde kaynağından arşivlendi.
- ^ Pellerito, John; Polak, Joseph F. (2012). Introduction to Vascular Ultrasonography (6. bas.). Elsevier Health Sciences. s. 559. ISBN .
- ^ . Scientific American. 8 Kasım 2010. 28 Mart 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Haziran 2015.
- ^ Weisstein, Eric W. . MathWorld--A Wolfram Web Resource. 20 Mayıs 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Mayıs 2018.
Dış bağlantılar
- . 23 Aralık 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Mart 2021.
- John D. Cook (27 Kasım 2018). . 27 Şubat 2019 tarihinde kaynağından arşivlendi.
- Dan Mosher. "Prolate Spheroid". Geogebra. 1 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 29 Aralık 2020.
- "Matlab Reference Spheroids". MathWorks. 1 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 29 Aralık 2020.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Dikey donme eksenli sferoidler basik oblate kutuplarda uzatilmis prolate Bir sferoit kuremsi veya donel elipsoit bir elipsin ana eksenlerinden biri etrafinda dondurulmesiyle elde edilen kuadrik bir yuzeydir baska bir deyisle iki esit yaricapa sahip bir elipsoitdir Bir sferoit sahiptir Elips ana ekseni etrafinda dondurulurse sonuc bir Amerikan futbolu veya ragbi topu biciminde sekillendirilmis kutuplarda uzatilmis prolate bir sferoittir Elips kucuk ekseni etrafinda dondurulurse sonuc mercimek seklinde yassi duzlestirilmis oblate bir sferoittir Cismi olusturan elips bir daire ise sonuc kuredir Yercekimi ve donmenin birlesik etkileri nedeniyle Dunya nin sekli ve tum gezegenlerin tam olarak bir kure degildir bunun yerine donus ekseni yonunde hafifce duzlestirilmistir Bu nedenle haritacilik ve jeodezide Dunya ya genellikle bir kure yerine referans elipsoid olarak bilinen basik bir sferoit olarak yaklasilir Mevcut Dunya Jeodezik Sistemi modeli yaricapi Ekvatorda 6 378137 km 3 963191 mi ve kutuplarda 6 356752 km 3 949903 mi olan bir sferoit kullanir Sferoid kelimesi aslinda iki veya uc eksenli elipsoidal seklin otesinde duzensizlikleri kabul eden yaklasik olarak kuresel bir govde anlamina geliyordu ve bu terim jeodezi hakkindaki bazi eski makalelerde ornegin Yeryuzunun kesik kuresel harmonik genislemelerine atifta bulunarak bu sekilde kullanilmaktadir DenklemiBir kureye yari eksenlerin atanmasi Eger c lt a solda ise kutuplardan basik oldugu durum oblate ve eger c gt a sagda ise kutuplara dogru uzatilmis olan durum prolate soz konusudur Koordinat eksenleri boyunca hizalanmis a b ve c yari eksenleri ile orijinde merkezlenmis uc eksenli bir elipsoidin denklemi x2a2 y2b2 z2c2 1 displaystyle frac x 2 a 2 frac y 2 b 2 frac z 2 c 2 1 Bir sferoidin simetri ekseni olarak z alinirsa ve a b olarak ayarlanirsa denklemi asagidaki sekilde verilir x2 y2a2 z2c2 1 displaystyle frac x 2 y 2 a 2 frac z 2 c 2 1 Yari eksen a sferoitin ekvator yaricapidir ve c simetri ekseni boyunca merkezden kutba olan mesafedir Olasi iki durum vardir c lt a kutuplardan basik oblate sferoit c gt a kutuplara dogru uzatilmis prolate sferoit a c durumu ise bir kureye indirgenir OzellikleriAlan c lt a olan yassi bir sferoid asagidaki yuzey alanina sahiptir Soblate 2pa2 1 1 e2eartanhe 2pa2 pc2eln 1 e1 e wheree2 1 c2a2 displaystyle S rm oblate 2 pi a 2 left 1 frac 1 e 2 e text artanh e right 2 pi a 2 pi frac c 2 e ln left frac 1 e 1 e right quad mbox where quad e 2 1 frac c 2 a 2 Yassi sferoit yari buyuk ekseni a ve yari kucuk ekseni c olan bir elipsin z ekseni etrafinda donerek olusturulur bu nedenle e eksantriklik olarak tanimlanabilir Bkz Elips c gt a olan bir kutuplara dogru uzatilmis sferoit asagidaki yuzey alanina sahiptir Sprolate 2pa2 1 caearcsine wheree2 1 a2c2 displaystyle S rm prolate 2 pi a 2 left 1 frac c ae arcsin e right qquad mbox where qquad e 2 1 frac a 2 c 2 Kutuplara dogru uzatilmis prolate sferoit yari buyuk ekseni c ve yari kucuk ekseni a ile bir elipsin z ekseni etrafinda donerek olusturulur bu nedenle e yine eksantriklik olarak tanimlanabilir Bkz Elips Bu formuller Sbasik formulu ayni sekilde uzatilmis kuremsi ve yardimcisi yuzey alaninin hesaplanmasi icin ayni sekilde kullanilabilir Bununla birlikte e daha sonra sanal hale gelir ve artik dogrudan eksantriklikle tanimlanamaz Bu sonuclarin her ikisi de standart matematiksel ozdeslikler ve elipsin parametreleri arasindaki iliskiler kullanilarak bircok baska bicime donusturulebilir Hacim Bir kuremsi icindeki hacim 4p3a2c 4 19a2c displaystyle frac 4 pi 3 a 2 c approx 4 19a 2 c Eger A 2a displaystyle A 2a ekvator capi ve C 2c displaystyle C 2c polar cap ise hacim p6A2C 0 523A2C displaystyle frac pi 6 A 2 C approx 0 523A 2 C dir Egrilik Bir sferoit asagidaki sekilde parametrik olarak ifade edilmisse s b l acos bcos l acos bsin l csin b displaystyle vec sigma beta lambda a cos beta cos lambda a cos beta sin lambda c sin beta burada b azaltilmis veya parametrik enlem l boylam p 2 lt b lt p 2 ve p lt l lt p olmak uzere asagidaki sekilde hesaplanir K b l c2 a2 c2 a2 cos2 b 2 displaystyle K beta lambda c 2 over left a 2 left c 2 a 2 right cos 2 beta right 2 ve ise asagidaki sekilde hesaplanir H b l c 2a2 c2 a2 cos2 b 2a a2 c2 a2 cos2 b 32 displaystyle H beta lambda c left 2a 2 left c 2 a 2 right cos 2 beta right over 2a left a 2 left c 2 a 2 right cos 2 beta right frac 3 2 Bu egriliklerin her ikisi de her zaman pozitiftir boylece bir sfero uzerindeki her nokta eliptiktir En boy orani Bir yassi sferoidin elipsin c a kutupsal uzunluklarin ekvatoryal uzunluklara oranidir ayni zamanda basiklik olarak da adlandirilir f ekvator kutup uzunlugu farkinin ekvator uzunluguna oranidir f a ca 1 ca displaystyle f frac a c a 1 frac c a Ilk eksantriklik genellikle yukaridaki gibi basitce eksantriklik genellikle yassilasma yerine kullanilir Su sekilde tanimlanir e 1 c2a2 displaystyle e sqrt 1 frac c 2 a 2 Eksantriklik ve basiklik arasindaki iliskiler sunlardir e 2f f2 displaystyle e sqrt 2f f 2 f 1 1 e2 displaystyle f 1 sqrt 1 e 2 Tum modern jeodezik elipsoidler yari buyuk eksen ile birlikte yari kucuk eksen en boy oranini verir duzlestirme veya ilk eksantriklik ile tanimlanir Bu tanimlar matematiksel olarak birbirinin yerine kullanilabilirken gercek dunyadaki hesaplamalarin bir miktar kesinlik kaybetmesine neden olur Karisikligi onlemek icin elipsoidal bir tanim kendi degerlerinin verdigi bicimde kesin oldugunu kabul eder UygulamalariBir atom cekirdegindeki protonlarin ve notronlarin yogunluk dagilimi icin en yaygin sekiller kuresel uzatilmis ve basik sferoidaldir burada kutup ekseninin donme ekseni veya donme acisal momentum vektorunun yonu oldugu varsayilir Protonlar arasindaki elektromanyetik itme yuzey gerilimi ve kuantum kabuk etkileri arasindaki rekabetin bir sonucu olarak deforme nukleer sekiller olusur Basik sferoitler Jupiter gezegeni 0 06487 ile basik bir sferoittir Basik sferoit Dunya Saturn Jupiter ve hizla donen yildiz Altair dahil olmak uzere donen gezegenlerin ve diger gok cisimlerinin yaklasik seklidir Saturn 0 09796 ile Gunes Sistemindeki en uzatilmis gezegendir in sarkac deneylerinden ve Christiaan Huygens in teorilerinden yola cikan aydinlanma bilimcisi Isaac Newton Jupiter ve Dunya nin merkezkac kuvveti nedeniyle basik sferoidler oldugunu dusundu Dunyanin cesitli kartografik ve jeodezik sistemleri tumu basik olan referans elipsoidlere dayanmaktadir Son derece uzatilmis bir gezegenin Bilimkurgu ornegi in romanindan dir Uzatilmis sferoidler Bir Avustralya futbolu kurallari Uzatilmis sferoid ragbi futbolu gibi cesitli spor dallarinda topun yaklasik seklidir Aslinda uc eksenli Elipsoitler olsalar da Gunes Sisteminin cesitli uydulari yaklasik uzatilmis sferoidler seklindedir Ornekler Saturn un uydulari Mimas Enceladus ve Tethys ile Uranus un uydusu Miranda dir Gok cisimleri yakin bir yorungede devasa bir cismin yorungesinde donduklerinde sekilleri hizli donme yoluyla baskin sferoitlere dogru bozulmanin aksine gelgit kuvvetleri yoluyla hafifce uzatilmis sferoitlere dogru bozulur En uc ornek Jupiter in uydusu Io dur ve hafif bir eksantriklik nedeniyle yorungesinde az cok uzatilarak yogun volkanizmaya neden olur Uzatilmis sferoitin ana ekseni bu durumda uydunun kutuplarindan gecmez ekvator uzerindeki iki noktadan dogrudan oncule dogru ve uzaga bakan iki noktadan gecer Terim ayrica Yengec Bulutsusu gibi bazi bulutsularin seklini tanimlamak icin de kullanilir Uzayda dalga yayilmasini ve girisimi analiz etmek icin kullanilan bir verici ile alici arasindaki dogrudan gorus hatti boyunca hizalanmis ana eksenlere sahip bir dizi es merkezli uzatilmis sferoidlerdir Atom cekirdeklerinin ve aktinit ve lantanit elemanlari uzatilmis sferoidler seklinde bicimlendirilmistir Anatomide testis gibi sferoidlere yakin organlar uzun ve kisa eksenleri ile olculebilir Bircok denizalti uzatilmis sferoit olarak tanimlanabilecek bir sekle sahiptir Dinamik ozellikler Duzgun yogunluga sahip bir sferoit icin eylemsizlik momenti ek bir simetri eksenine sahip bir elipsoidinkidir Bir sferoitin ana ekseni c ve kucuk eksenleri a ve b olarak tanimlandiginda bu ana eksenler boyunca eylemsizlik momentleri C A ve B dir Bununla birlikte bir sferoidde kucuk eksenler simetriktir Bu nedenle ana eksenler boyunca eylemsizlik terimleri sunlardir A B 15M a2 c2 displaystyle A B frac 1 5 M a 2 c 2 C 15M a2 a2 25M a2 displaystyle C frac 1 5 M a 2 a 2 frac 2 5 M a 2 burada M cismin kutlesi olarak tanimlanir M 43prca2 displaystyle M frac 4 3 pi rho ca 2 Ayrica bakinizKaynakca 8 Ekim 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 29 Aralik 2020 Torge Wolfgang 2001 Geodesy 3 bas Berlin New York s 104 ISBN 978 3 11 017072 6 OCLC 46641599 Bu sonucun bir turevi su adreste bulunabilir Mathworld wolfram com 3 Eylul 2000 tarihinde kaynagindan arsivlendi Erisim tarihi 24 Haziran 2014 Bu sonucun bir turevi su adreste bulunabilir Mathworld wolfram com 7 Ekim 2003 21 Haziran 2000 tarihinde kaynagindan arsivlendi Erisim tarihi 24 Haziran 2014 Brial Pierre Shaalan Cecile Kasim 2009 Introduction a la Geodesie et au Geopositionnement par satellites PDF Fransizca s 8 doi 10 13140 RG 2 2 30646 86085 30 Ekim 2020 tarihinde kaynagindan PDF erisim tarihi 29 Aralik 2020 Greenburg John L 1995 Isaac Newton and the Problem of the Earth s Shape History of Exact Sciences Springer 49 4 371 391 doi 10 1007 BF00374704 JSTOR 41134011 Durant Will Durant Ariel 28 Temmuz 1997 The Story of Civilization The Age of Louis XIV MJF Books ISBN 1567310192 Ekim 1973 The Distance to the Crab Nebula and NP 0532 Publications of the Astronomical Society of the Pacific 85 507 s 579 Bibcode 1973PASP 85 579T doi 10 1086 129507 Encyclopedia Britannica 7 Eylul 2015 tarihinde kaynagindan arsivlendi Pellerito John Polak Joseph F 2012 Introduction to Vascular Ultrasonography 6 bas Elsevier Health Sciences s 559 ISBN 9781455737666 Scientific American 8 Kasim 2010 28 Mart 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 13 Haziran 2015 Weisstein Eric W MathWorld A Wolfram Web Resource 20 Mayis 2000 tarihinde kaynagindan arsivlendi Erisim tarihi 16 Mayis 2018 Dis baglantilar 23 Aralik 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 8 Mart 2021 John D Cook 27 Kasim 2018 27 Subat 2019 tarihinde kaynagindan arsivlendi Dan Mosher Prolate Spheroid Geogebra 1 Nisan 2021 tarihinde kaynagindan Erisim tarihi 29 Aralik 2020 Matlab Reference Spheroids MathWorks 1 Nisan 2021 tarihinde kaynagindan Erisim tarihi 29 Aralik 2020
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans