Matematikte zeta sabiti, bir tam sayının Riemann zeta fonksiyonunda yerine yazılmasıyla elde edilen sayıdır. Bu madde farklı tam sayı değerleri için zeta fonksiyonu özdeşlikleri içermektedir.
0 ve 1'de Riemann zeta fonksiyonu
eşitliği geçerlidir. 1 noktasında bir kutup bulunur.
Pozitif tam sayılar
Pozitif çift tam sayılar
Pozitif çift tam sayılar kümesi Euler tarafından bulunan ve Bernoulli sayılarıyla ilintilendirilen şu özdeşliği içerir:
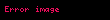
; Bu eşitliğin gösterimi Basel problemi olarak da bilinir.
; Fizikteki ve .
Pozitif çift tam sayılardaki zeta ile Bernoulli sayıları arasındaki ilişki şu şekilde yazılabilir:
Burada 

| 2n | A | B |
|---|---|---|
| 2 | 6 | 1 |
| 4 | 90 | 1 |
| 6 | 945 | 1 |
| 8 | 9450 | 1 |
| 10 | 93555 | 1 |
| 12 | 638512875 | 691 |
| 14 | 18243225 | 2 |
| 16 | 325641566250 | 3617 |
| 18 | 38979295480125 | 43867 |
| 20 | 1531329465290625 | 174611 |
| 22 | 13447856940643125 | 155366 |
| 24 | 201919571963756521875 | 236364091 |
| 26 | 11094481976030578125 | 1315862 |
| 28 | 564653660170076273671875 | 6785560294 |
| 30 | 5660878804669082674070015625 | 6892673020804 |
| 32 | 62490220571022341207266406250 | 7709321041217 |
| 34 | 12130454581433748587292890625 | 151628697551 |
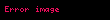
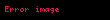
eşitliği sağlanır ve özyinelemeli çözümle
ifadesine ulaşılır.
Bu özyinelemeli ilişki Bernoulli sayılarından da bulunabilir.
Çift sayılarda geçerli olan dizi, 0 noktası yakınında kotanjant fonksiyonunun Laurent açılımı yardımıyla da elde edilebilir.
Pozitif tek tam sayılar
İlk birkaç tek doğal sayı için
eşitlikleri sağlanır.
ζ(3) () ve ζ(2n+1) (n ∈ N) kümesinin sonsuz çoklukta elemanının irrasyonel olduğu bilinmektedir. Riemann zeta fonksiyonunun da pozitif tek sayılar kümesinin kimi alt kümeleri için irrasyonel elemanlara sahip olduğu gözlenmiştir. Örneğin; ζ(5), ζ(7), ζ(9) ve ζ(11)'den en az birinin irrasyonel olduğu kesindir.
Bir bölümü aşağıda verilen özdeşliklerin çoğu tarafından bulunmuştur. Bu özdeşliklerin kayda değer yanı çok hızlı yakınsamaları ve üç basamağa varan kesinlik oranına ulaşmalarıdır.
ζ(5)
Plouffe
ve
özdeşliklerini bulmuştur.
ζ(7)
Toplam, biçiminde verilmiştir.
ζ(2n+1)
şeklinde tanımlanan büyüklükler
biçiminde ilişki dizileri verir. Burada 

| n | A | B | C | D |
|---|---|---|---|---|
| 3 | 180 | 7 | 360 | 0 |
| 5 | 1470 | 5 | 3024 | 84 |
| 7 | 56700 | 19 | 113400 | 0 |
| 9 | 18523890 | 625 | 37122624 | 74844 |
| 11 | 425675250 | 1453 | 851350500 | 0 |
| 13 | 257432175 | 89 | 514926720 | 62370 |
| 15 | 390769879500 | 13687 | 781539759000 | 0 |
| 17 | 1904417007743250 | 6758333 | 3808863131673600 | 29116187100 |
| 19 | 21438612514068750 | 7708537 | 42877225028137500 | 0 |
| 21 | 1881063815762259253125 | 68529640373 | 3762129424572110592000 | 1793047592085750 |
Bu sabitler Bernoulli sayıları toplamı biçiminde de yazılabilir.
Negatif tam sayılar
Negatif tam sayılar için
eşitliği sağlanır.
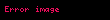
"açık sıfırlar" olarak adlandırılan değerlere negatif çift tam sayılarda rastlanır.
Negatif tek tam sayıların ilk birkaç değeri aşağıda verilmiştir.
Bu sayılar Bernoulli sayılarına benzer biçimde çok büyük negatif tek tam sayı değerleri için küçük değerlere sahip değillerdir. Bu değerlerin ilki için maddesine bakılabilir.
Türevleri
Zeta fonksiyonunun negatif çift tam sayılardaki türevi aşağıdaki gibidir.
Bu türevin ilk birkaç değeri şu şekildedir:
Aşağıdaki eşitlikler de sağlanır.
Burada 
Zeta Sabitleri Toplamı
Kaynakça
- , "Ramanujan'ın Not Defterinden Esinlenen Özdeşlikler30 Ocak 2009 tarihinde Wayback Machine sitesinde .", (1998).
- , "Ramanujan'ın Not Defterinden Esinlenen Özdeşlikler (2. Bölüm)4 Nisan 2009 tarihinde Wayback Machine sitesinde . PDF26 Eylül 2011 tarihinde Wayback Machine sitesinde ." (2006).
- Linas Vepstas, "Plouffe'nin Ramanujan Özdeşlikleri Üzerine9 Mayıs 2008 tarihinde Wayback Machine sitesinde .", ArXiv Math.NT/0609775 (2006).
- , "ζ(5), ζ(7), ζ(9), ζ(11)'den Biri İrrasyonel." Uspekhi Mat. Nauk 56, 149-150, 2001. PDF24 Ağustos 2007 tarihinde Wayback Machine sitesinde . PS24 Ağustos 2007 tarihinde Wayback Machine sitesinde . (Rusça) PDF16 Mart 2007 tarihinde Wayback Machine sitesinde . (Rusça) PS11 Mart 2007 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte zeta sabiti bir tam sayinin Riemann zeta fonksiyonunda yerine yazilmasiyla elde edilen sayidir Bu madde farkli tam sayi degerleri icin zeta fonksiyonu ozdeslikleri icermektedir 0 ve 1 de Riemann zeta fonksiyonuSifirda z 0 B1 12 displaystyle zeta 0 B 1 frac 1 2 esitligi gecerlidir 1 noktasinda bir kutup bulunur z 1 displaystyle zeta 1 infty Pozitif tam sayilarPozitif cift tam sayilar Pozitif cift tam sayilar kumesi Euler tarafindan bulunan ve Bernoulli sayilariyla ilintilendirilen su ozdesligi icerir z 2n 1 n 1B2n 2p 2n2 2n displaystyle zeta 2n 1 n 1 frac B 2n 2 pi 2n 2 2n n 1 displaystyle n geq 1 kosulunu saglayan birkac deger asagida verilmistir z 2 1 122 132 p26 1 6449 displaystyle zeta 2 1 frac 1 2 2 frac 1 3 2 cdots frac pi 2 6 1 6449 dots Bu esitligin gosterimi Basel problemi olarak da bilinir z 4 1 124 134 p490 1 0823 displaystyle zeta 4 1 frac 1 2 4 frac 1 3 4 cdots frac pi 4 90 1 0823 dots Fizikteki ve z 6 1 126 136 p6945 1 0173 displaystyle zeta 6 1 frac 1 2 6 frac 1 3 6 cdots frac pi 6 945 1 0173 dots z 8 1 128 138 p89450 1 00407 displaystyle zeta 8 1 frac 1 2 8 frac 1 3 8 cdots frac pi 8 9450 1 00407 dots z 10 1 1210 1310 p1093555 1 000994 displaystyle zeta 10 1 frac 1 2 10 frac 1 3 10 cdots frac pi 10 93555 1 000994 dots z 12 1 1212 1312 691p12638512875 1 000246 displaystyle zeta 12 1 frac 1 2 12 frac 1 3 12 cdots frac 691 pi 12 638512875 1 000246 dots z 14 1 1214 1314 2p1418243225 1 0000612 displaystyle zeta 14 1 frac 1 2 14 frac 1 3 14 cdots frac 2 pi 14 18243225 1 0000612 dots Pozitif cift tam sayilardaki zeta ile Bernoulli sayilari arasindaki iliski su sekilde yazilabilir 0 Anz n Bnpn displaystyle 0 A n zeta n B n pi n Burada An displaystyle A n ve Bn displaystyle B n tum cift n degerlerine karsilik gelen tam sayilardir Bu degerlerin bir bolumu asagidaki tabloda verilmistir Katsayilar 2n A B2 6 14 90 16 945 18 9450 110 93555 112 638512875 69114 18243225 216 325641566250 361718 38979295480125 4386720 1531329465290625 17461122 13447856940643125 15536624 201919571963756521875 23636409126 11094481976030578125 131586228 564653660170076273671875 678556029430 5660878804669082674070015625 689267302080432 62490220571022341207266406250 770932104121734 12130454581433748587292890625 151628697551 hn displaystyle eta n nin yukarida gosterildigi gibi B A displaystyle B A katsayisi olmasi durumunda z 2n ℓ 1 1ℓ2n hnp2n displaystyle zeta 2n sum ell 1 infty frac 1 ell 2n eta n pi 2n esitligi saglanir ve ozyinelemeli cozumle h1 16 displaystyle eta 1 frac 1 6 hn ℓ 1n 1 1 ℓ 1hn ℓ 2ℓ 1 1 n 1n 2n 1 displaystyle eta n sum ell 1 n 1 1 ell 1 frac eta n ell 2 ell 1 1 n 1 frac n 2n 1 ifadesine ulasilir Bu ozyinelemeli iliski Bernoulli sayilarindan da bulunabilir Cift sayilarda gecerli olan dizi 0 noktasi yakininda kotanjant fonksiyonunun Laurent acilimi yardimiyla da elde edilebilir p2cot px 12x 1 p26x p490x3 p6945x5 displaystyle frac pi 2 cot pi x frac 1 2 x 1 frac pi 2 6 x frac pi 4 90 x 3 frac pi 6 945 x 5 Pozitif tek tam sayilar Ilk birkac tek dogal sayi icin z 1 1 12 13 displaystyle zeta 1 1 frac 1 2 frac 1 3 cdots infty Harmonik seri z 3 1 123 133 1 20205 displaystyle zeta 3 1 frac 1 2 3 frac 1 3 3 cdots 1 20205 dots Apery sabiti z 5 1 125 135 1 03692 displaystyle zeta 5 1 frac 1 2 5 frac 1 3 5 cdots 1 03692 dots z 7 1 127 137 1 00834 displaystyle zeta 7 1 frac 1 2 7 frac 1 3 7 cdots 1 00834 dots z 9 1 129 139 1 002008 displaystyle zeta 9 1 frac 1 2 9 frac 1 3 9 cdots 1 002008 dots esitlikleri saglanir z 3 ve z 2n 1 n N kumesinin sonsuz coklukta elemaninin irrasyonel oldugu bilinmektedir Riemann zeta fonksiyonunun da pozitif tek sayilar kumesinin kimi alt kumeleri icin irrasyonel elemanlara sahip oldugu gozlenmistir Ornegin z 5 z 7 z 9 ve z 11 den en az birinin irrasyonel oldugu kesindir Bir bolumu asagida verilen ozdesliklerin cogu tarafindan bulunmustur Bu ozdesliklerin kayda deger yani cok hizli yakinsamalari ve uc basamaga varan kesinlik oranina ulasmalaridir z 5 Plouffe z 5 1294p5 7235 n 1 1n5 e2pn 1 235 n 1 1n5 e2pn 1 displaystyle zeta 5 frac 1 294 pi 5 frac 72 35 sum n 1 infty frac 1 n 5 e 2 pi n 1 frac 2 35 sum n 1 infty frac 1 n 5 e 2 pi n 1 ve z 5 12 n 1 1n5sinh pn 3920 n 1 1n5 e2pn 1 120 n 1 1n5 e2pn 1 displaystyle zeta 5 12 sum n 1 infty frac 1 n 5 sinh pi n frac 39 20 sum n 1 infty frac 1 n 5 e 2 pi n 1 frac 1 20 sum n 1 infty frac 1 n 5 e 2 pi n 1 ozdesliklerini bulmustur z 7 z 7 1956700p7 2 n 1 1n7 e2pn 1 displaystyle zeta 7 frac 19 56700 pi 7 2 sum n 1 infty frac 1 n 7 e 2 pi n 1 Toplam biciminde verilmistir z 2n 1 S s n 1 1ns e2pn 1 displaystyle S pm s sum n 1 infty frac 1 n s e 2 pi n pm 1 seklinde tanimlanan buyuklukler 0 Anz n Bnpn CnS n DnS n displaystyle 0 A n zeta n B n pi n C n S n D n S n biciminde iliski dizileri verir Burada An Bn Cn displaystyle A n B n C n ve Dn displaystyle D n pozitif tam sayilardir Plouffe asagidaki degerleri de bulmustur Katsayilar n A B C D3 180 7 360 05 1470 5 3024 847 56700 19 113400 09 18523890 625 37122624 7484411 425675250 1453 851350500 013 257432175 89 514926720 6237015 390769879500 13687 781539759000 017 1904417007743250 6758333 3808863131673600 2911618710019 21438612514068750 7708537 42877225028137500 021 1881063815762259253125 68529640373 3762129424572110592000 1793047592085750 Bu sabitler Bernoulli sayilari toplami biciminde de yazilabilir Negatif tam sayilarNegatif tam sayilar icin z n Bn 1n 1 displaystyle zeta n frac B n 1 n 1 esitligi saglanir n 1 displaystyle n geq 1 icin acik sifirlar olarak adlandirilan degerlere negatif cift tam sayilarda rastlanir z 2n 0 displaystyle zeta 2n 0 Negatif tek tam sayilarin ilk birkac degeri asagida verilmistir z 1 112 displaystyle zeta 1 frac 1 12 z 3 1120 displaystyle zeta 3 frac 1 120 z 5 1252 displaystyle zeta 5 frac 1 252 z 7 1240 displaystyle zeta 7 frac 1 240 Bu sayilar Bernoulli sayilarina benzer bicimde cok buyuk negatif tek tam sayi degerleri icin kucuk degerlere sahip degillerdir Bu degerlerin ilki icin 1 2 3 4 maddesine bakilabilir TurevleriZeta fonksiyonunun negatif cift tam sayilardaki turevi asagidaki gibidir z 2n 1 n 2n 2 2p 2nz 2n 1 displaystyle zeta prime 2n 1 n frac 2n 2 2 pi 2n zeta 2n 1 Bu turevin ilk birkac degeri su sekildedir z 2 z 3 4p2 displaystyle zeta prime 2 frac zeta 3 4 pi 2 z 4 34p4z 5 displaystyle zeta prime 4 frac 3 4 pi 4 zeta 5 z 6 458p6z 7 displaystyle zeta prime 6 frac 45 8 pi 6 zeta 7 z 8 3154p8z 9 displaystyle zeta prime 8 frac 315 4 pi 8 zeta 9 Asagidaki esitlikler de saglanir z 0 12log 2p 0 918938533 displaystyle zeta prime 0 frac 1 2 log 2 pi approx 0 918938533 ldots z 1 112 log A 0 165421137 displaystyle zeta prime 1 frac 1 12 log A approx 0 165421137 ldots Burada A displaystyle A karsilik gelmektedir Zeta Sabitleri Toplami k 2 z k 1 1 displaystyle sum k 2 infty zeta k 1 1 Kaynakca Ramanujan in Not Defterinden Esinlenen Ozdeslikler30 Ocak 2009 tarihinde Wayback Machine sitesinde 1998 Ramanujan in Not Defterinden Esinlenen Ozdeslikler 2 Bolum 4 Nisan 2009 tarihinde Wayback Machine sitesinde PDF26 Eylul 2011 tarihinde Wayback Machine sitesinde 2006 Linas Vepstas Plouffe nin Ramanujan Ozdeslikleri Uzerine9 Mayis 2008 tarihinde Wayback Machine sitesinde ArXiv Math NT 0609775 2006 z 5 z 7 z 9 z 11 den Biri Irrasyonel Uspekhi Mat Nauk 56 149 150 2001 PDF24 Agustos 2007 tarihinde Wayback Machine sitesinde PS24 Agustos 2007 tarihinde Wayback Machine sitesinde Rusca PDF16 Mart 2007 tarihinde Wayback Machine sitesinde Rusca PS11 Mart 2007 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State