Matematiğin bir alt dalı olan karmaşık analizde ve çok değişkenli karmaşık analizde Wirtinger operatörleri ya da Wirtinger türev operatörleri karmaşık düzlemdeki ya da karmaşık koordinat uzayındaki üzerinde tanımlı holomorf, tersholomorf ya da sadece türevli fonksiyonlara uygulanabilen birinci mertebeden kısmi türev operatörleridir. Bu operatörlerin bu çeşit fonksiyonlara uygulanması sonucu ortaya çıkan fonksiyonlara bu fonksiyonların Wirtinger türevleri adı verilir.
Wirtinger türevlerinin gerçel değişkenli fonksiyonların türevi için verilen tanım ve özellikleri karmaşık düzlemde veya ya da karmaşık koordinat uzayında tanımlı fonksiyonlara taşıyan bir doğası vardır. Operatörler ve türevler adını, bu kavramları 1927 yılında Birkaç karmaşık değişkenli fonksiyonların formel teorisi üzerine başlıklı makalesinde sistematik bir biçimde ilk defa ele alan Wilhelm Wirtinger'in adını taşımaktadır.
Tarihçe
Erken dönem (1899–1911): Henri Poincaré'nin çalışmaları
Cherry & Ye (2001, s. 31) ve Remmert (1991, ss. 66–67)'de kısaca bahsedildiği gibi, Wirtinger türevlerinin karmaşık analizdeki kullanımı en azından Poincaré 1899'a kadar gitmektedir. 1899'daki makalesinin üçüncü paragrafında,Henri Poincaré ilk önce 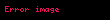
Bu tanımdan sonra, daha önceden 


Belli ki, bu makale çok değişkenli karmaşık analizde çalışan araştırmacılar tarafından gözden kaçırılmış ya da dikkate alınmamış. Çünkü, Levi-Civita (1905), Levi (1910) (Levi 1911) ve Amoroso (1912) gibi erken dönem makalelerin hepsinde bütün temel kısmî türev operatörler gerçel değişkenler aracılığıyla yazılmış. Daha sonraları, ilk defa 1913'de baskısı yapılan ve 1966da tekrar baskısı yapılan Osgood 1966'da bile, karmaşık değişkenlere göre kısmî türevlere bile formel türev olarak bakılmaktadır. Bu bağlamda, çokluharmonik operatör ve Levi operatörleri için, Osgood'un, , Levi ve Levi-Civita'nın yolunu takip etmektedir.
Dimitrie Pompeiu'nun 1912 ve 1913'teki çalışmaları
Henrici (1993, s. 294) kaynağına göre kavramın tanımlanmasında yeni bir adım tarafından Pompeiu 1912 makalesinde atıldı. Bu makalede, bir 

Burada, 



Wilhelm Wirtinger'in çalışması
Wirtinger türevlerinin ilk sistematik sunumunun çok karmaşık değişkenli fonksiyonlar teorisinde ortaya çıkan niceliklerin hesaplanmasını basitleştirmek için Wilhelm Wirtinger'in Wirtinger 1927 makalesinde ortaya atıldığı anlaşılıyor: bu diferansiyel operatörlerin literatüre sokulması sonucunda, ve gibi teoride yaygın olarak kullanılan tüm diferansiyel operatörlerin gösterimi önemli ölçüde basitleştirilmiş ve dolayısıyla kullanımı daha kolay hale gelmiştir. Makale, kasıtlı olarak biçimsel bir bakış açısıyla, yâni, çıkarılan özelliklerin kesin bir çıkarımı verilmeden yazılmıştır.
Tanım
Tanımın altında yatan fikir
Karmaşık düzlemdeki açık bir küme üzerinde tanımlı ve gerçel değişkenlere göre türevlerinin varlığı bilinen bir 
olarak yazalım. Eğer 

ve
olacaktır. O hâlde, türev almanın doğrusallığıyla
ve
yazılabilir. Sonuç olarak, yukarıdaki (toplam) diferansiyel ifadesi tekrar düzenlenerek
yazılabilir. O zaman,
ve
.
tanımlanırsa,
yazılabilir.
Tanımın resmi ifadesi
Karmaşık düzlemde tanım
Karmaşık sayılar için 






ve
şeklinde yazılabilir. Bu hâlde, 
ve
.
olarak tanımlanır. Wirtinger türevlerinin tanımını veren
ve
kısmî diferansiyel operatörlerine Wirtinger türev operatörleri ya da sadece Wirtinger operatörleri denilir.
Wirtinger operatörlerinin tanım kümesi en doğal hâliyle türevlenebilir fonksiyonları içermektedir. Ancak, operatörler doğrusal oldukları ve sabit katsayılara sahip oldukları için, tanım kümeleri genelleştirilmiş fonksiyonların her türlü uzayına da genişletilebilir.
Karmaşık koordinat uzayında tanım
Yukarıda verilen ve bir karmaşık değişkenli fonksiyonlar için tanımlanan Wirtinger operatörlerinin tanımı yüksek boyutta tanımlı ve karmaşık değerler alan fonksiyonlar için de verilebilir. 

Karmaşık türevlenebilme ile ilişkisi
Bir fonksiyon bir noktada karmaşık türevlenebilir ise, fonksiyonun Wirtinger türevi, Cauchy-Riemann denklemleri sayesinde fonksiyonun karmaşık türevine eşittir. Gerçekten de eğer bir 

Wirtinger türevinin tanımıyla başlayarak ve Cauchy-Riemann denklemleri kullanarak
elde edilir.
Wirtinger türevinin karmaşık eşlenik değişkendeki hâli de yine karmaşık türevlenebilmeyle alâkalıdır. 
Cauchy-Riemann operatörü







elde edildiği gibi, 


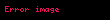



ve
tanımlanabilir. O zaman,
elde edilir. Holomorfluk durumunda, 


Özellikler
Aşağıda verilen özelliklerde 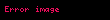

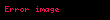



Doğrusallık



Çarpma kuralı



Zincir kuralı
Zincir kuralının iki hâli için, 



Bir karmaşık değişkenli fonksiyonlar için zincir kuralı


n > 1 karmaşık değişkenli fonksiyonlar için zincir kuralı



Eşlenik alma altına Wirtinger operatörleri


Notlar ve kaynakça
- ^ (1986), "Unification of global and local existence theorems for holomorphic functions of several complex variables", Memorie della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8, 18 (3), ss. 61-83, MR 0917525, Zbl 0705.32006
- ^ Kracht, Manfred; (1988), Methods of Complex Analysis in Partial Differential Equations and Applications, Series of Monographs and Advanced Texts, New York–Chichester–Brisbane–Toronto–Singapore: , ss. xiv+394, ISBN , MR 0941372, Zbl 0644.35005
- ^ Wirtinger, Wilhelm (1927), "Zur formalen Theorie der Funktionen von mehr komplexen Veränderlichen" [Birkaç karmaşık değişkenli fonksiyonların formel teorisi üzerine], (Almanca), 97 (1), ss. 357-375, doi:10.1007/BF01447872, JFM 52.0342.03
- ^ Poincaré 1899, ss. 111–114'e bakınız
- ^ Bu fonksiyonlar, aslında bugün çokluharmonik denilen fonksiyonlardır.
- (1969), "Derivata areolare e funzioni a variazione limitata", (İtalyanca), XIV (1), ss. 27-37, MR 0265616, Zbl 0201.10002.
- Levi, Eugenio Elia (1910), "Studii sui punti singolari essenziali delle funzioni analitiche di due o più variabili complesse", , s. III (İtalyanca), XVII (1), ss. 61-87, doi:10.1007/BF02419336, JFM 41.0487.01.
- Levi, Eugenio Elia (1911), "Sulle ipersuperficie dello spazio a 4 dimensioni che possono essere frontiera del campo di esistenza di una funzione analitica di due variabili complesse", , s. III (İtalyanca), XVIII (1), ss. 69-79, doi:10.1007/BF02420535, JFM 42.0449.02.
- (1905), "Sulle funzioni di due o più variabili complesse", Rendiconti della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 5 (İtalyanca), XIV (2), ss. 492-499, JFM 36.0482.01.
- Osgood, William Fogg (1966) [1913], Topics in the theory of functions of several complex variables (unabridged and corrected bas.), New York: Dover, ss. IV+120, JFM 45.0661.02, MR 0201668, Zbl 0138.30901.
- (1993) [1986], Applied and Computational Complex Analysis Volume 3, Wiley Classics Library (Reprint bas.), New York–Chichester–Brisbane–Toronto–Singapore: , ss. X+637, ISBN , MR 0822470, Zbl 1107.30300.
- Poincaré, H. (1899), "Sur les propriétés du potentiel et sur les fonctions Abéliennes", (Fransızca), 22 (1), ss. 89-178, doi:10.1007/BF02417872, JFM 29.0370.02.
- (1912), "Sur une classe de fonctions d'une variable complexe", (Fransızca), 33 (1), ss. 108-113, doi:10.1007/BF03015292, JFM 43.0481.01.
- (1913), "Sur une classe de fonctions d'une variable complexe et sur certaines équations intégrales", (Fransızca), 35 (1), ss. 277-281, doi:10.1007/BF03015607.
- Vekua, I. N. (1962), Generalized Analytic Functions, International Series of Monographs in Pure and Applied Mathematics, 25, London–Paris–Frankfurt: Pergamon Press, ss. xxx+668, MR 0150320, Zbl 0100.07603
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan karmasik analizde ve cok degiskenli karmasik analizde Wirtinger operatorleri ya da Wirtinger turev operatorleri karmasik duzlemdeki ya da karmasik koordinat uzayindaki uzerinde tanimli holomorf tersholomorf ya da sadece turevli fonksiyonlara uygulanabilen birinci mertebeden kismi turev operatorleridir Bu operatorlerin bu cesit fonksiyonlara uygulanmasi sonucu ortaya cikan fonksiyonlara bu fonksiyonlarin Wirtinger turevleri adi verilir Wirtinger turevlerinin gercel degiskenli fonksiyonlarin turevi icin verilen tanim ve ozellikleri karmasik duzlemde veya ya da karmasik koordinat uzayinda tanimli fonksiyonlara tasiyan bir dogasi vardir Operatorler ve turevler adini bu kavramlari 1927 yilinda Birkac karmasik degiskenli fonksiyonlarin formel teorisi uzerine baslikli makalesinde sistematik bir bicimde ilk defa ele alan Wilhelm Wirtinger in adini tasimaktadir TarihceErken donem 1899 1911 Henri Poincare nin calismalari Cherry amp Ye 2001 s 31 ve Remmert 1991 ss 66 67 de kisaca bahsedildigi gibi Wirtinger turevlerinin karmasik analizdeki kullanimi en azindan Poincare 1899 a kadar gitmektedir 1899 daki makalesinin ucuncu paragrafinda Henri Poincare ilk once Cn displaystyle mathbb C n deki karmasik degiskeni ve bu degiskenin karmasik eslenigini soyle tanimliyor xk iyk zkxk iyk uk1 k n displaystyle begin cases x k iy k z k x k iy k u k end cases qquad 1 leqslant k leqslant n Bu tanimdan sonra daha onceden xk yq displaystyle x k y q k q 1 n displaystyle k q 1 cdots n gercel degiskenleri araciligiyla yazilmis olan ve biharmonik biharmonique dedigi V displaystyle V fonksiyonlarini tanimlayan denklemleri bu yeni degiskenlerde yaziyor d2Vdzkduq 0 displaystyle frac d 2 V dz k du q 0 Belli ki bu makale cok degiskenli karmasik analizde calisan arastirmacilar tarafindan gozden kacirilmis ya da dikkate alinmamis Cunku Levi Civita 1905 Levi 1910 Levi 1911 ve Amoroso 1912 gibi erken donem makalelerin hepsinde butun temel kismi turev operatorler gercel degiskenler araciligiyla yazilmis Daha sonralari ilk defa 1913 de baskisi yapilan ve 1966da tekrar baskisi yapilan Osgood 1966 da bile karmasik degiskenlere gore kismi turevlere bile formel turev olarak bakilmaktadir Bu baglamda cokluharmonik operator ve Levi operatorleri icin Osgood un Levi ve Levi Civita nin yolunu takip etmektedir Dimitrie Pompeiu nun 1912 ve 1913 teki calismalari Henrici 1993 s 294 kaynagina gore kavramin tanimlanmasinda yeni bir adim tarafindan Pompeiu 1912 makalesinde atildi Bu makalede bir z0 C displaystyle z 0 in mathbb C noktasi etrafinda tanimli ve karmasik degerler alan bir g z displaystyle g z fonksiyonu icin areolar turevi su sekilde tanimlanmistir g z z0 tan limr 012pir2 G z0 r g z dz displaystyle frac partial g partial bar z z 0 mathrel overset mathrm tan lim r to 0 frac 1 2 pi ir 2 oint Gamma z 0 r g z mathrm d z Burada G z0 r D z0 r displaystyle Gamma z 0 r partial D z 0 r yani z0 displaystyle z 0 merkezli ve r displaystyle r yaricapli bir diskin topolojik siniridir ve fonksiyonun tanimli oldugu bolgenin icindedir Bu tanim karmasik eslenik degiskene gore Wirtinger turevinin alternatif bir tanimidir Henrici 1993 s 294 tarafindan belirtildigi gibi limit z z0 displaystyle z z 0 noktasinda ayni zamanda turevlenebilir olmayan fonksiyonlar icin de mevcut olabileceginden daha genel bir tanimdir Fichera 1969 s 28 e gore areolar turevini Sobolev anlaminda zayif bir turev olarak ilk tanimlayan Ilya Vekua dir Sonraki Pompeiu 1913 makalesinde Pompeiu bu gorece yeni tanimlanmis kavrami kullanarak Cauchy integral formulunun genellemesini elde eder Elde edilen bu formul artik Cauchy Pompeiu formulu olarak bilinmektedir Wilhelm Wirtinger in calismasi Wirtinger turevlerinin ilk sistematik sunumunun cok karmasik degiskenli fonksiyonlar teorisinde ortaya cikan niceliklerin hesaplanmasini basitlestirmek icin Wilhelm Wirtinger in Wirtinger 1927 makalesinde ortaya atildigi anlasiliyor bu diferansiyel operatorlerin literature sokulmasi sonucunda ve gibi teoride yaygin olarak kullanilan tum diferansiyel operatorlerin gosterimi onemli olcude basitlestirilmis ve dolayisiyla kullanimi daha kolay hale gelmistir Makale kasitli olarak bicimsel bir bakis acisiyla yani cikarilan ozelliklerin kesin bir cikarimi verilmeden yazilmistir TanimTanimin altinda yatan fikir Karmasik duzlemdeki acik bir kume uzerinde tanimli ve gercel degiskenlere gore turevlerinin varligi bilinen bir f displaystyle f fonksiyonunun toplam diferansiyelini df f xdx f ydy displaystyle mathrm d f frac partial f partial x mathrm d x frac partial f partial y mathrm d y olarak yazalim Eger z x iy displaystyle z x mathrm i y ve z x iy displaystyle bar z x mathrm i y alirsak o zaman x 12 z z displaystyle textstyle x frac 1 2 z bar z ve y 12i z z i2 z z displaystyle textstyle y frac 1 2 mathrm i z bar z frac mathrm i 2 bar z z olacaktir O halde turev almanin dogrusalligiyla dx 12 dz dz displaystyle mathrm d x frac 1 2 mathrm d z mathrm d bar z ve dy i2 dz dz displaystyle mathrm d y frac mathrm i 2 mathrm d bar z mathrm d z yazilabilir Sonuc olarak yukaridaki toplam diferansiyel ifadesi tekrar duzenlenerek df 12 f x i f y dz 12 f x i f y dz displaystyle mathrm d f frac 1 2 left frac partial f partial x mathrm i frac partial f partial y right mathrm d z frac 1 2 left frac partial f partial x mathrm i frac partial f partial y right mathrm d bar z yazilabilir O zaman f z 12 f x i f y displaystyle frac partial f partial z frac 1 2 left frac partial f partial x mathrm i frac partial f partial y right ve f z 12 f x i f y displaystyle frac partial f partial bar z frac 1 2 left frac partial f partial x mathrm i frac partial f partial y right tanimlanirsa df f zdz f z dz displaystyle mathrm d f frac partial f partial z mathrm d z frac partial f partial bar z mathrm d bar z yazilabilir Tanimin resmi ifadesi Karmasik duzlemde tanim Karmasik sayilar icin z C displaystyle z in mathbb C degiskenini gercel x displaystyle x ve y displaystyle y degiskenleri uzerinden z x iy displaystyle z x mathrm i y olarak tanimlayalim G R2 displaystyle G subset mathbb R 2 de acik kume olsun ve f u iv G C displaystyle f u mathrm i v colon G to mathbb C ise gercel degiskenlerde turevlenebilir bir fonksiyon olsun O zaman f displaystyle f fonksiyonunun kismi turevleri vardir Bu kismi turevler f x u x i v x displaystyle frac partial f partial x frac partial u partial x mathrm i frac partial v partial x ve f y u y i v y displaystyle frac partial f partial y frac partial u partial y mathrm i frac partial v partial y seklinde yazilabilir Bu halde f displaystyle f fonksiyonunun Wirtinger turevleri f z 12 f x i f y displaystyle frac partial f partial z frac 1 2 left frac partial f partial x mathrm i frac partial f partial y right ve f z 12 f x i f y displaystyle frac partial f partial bar z frac 1 2 left frac partial f partial x mathrm i frac partial f partial y right olarak tanimlanir Wirtinger turevlerinin tanimini veren z 12 x i y displaystyle frac partial partial z frac 1 2 left frac partial partial x mathrm i frac partial partial y right ve z 12 x i y displaystyle frac partial partial bar z frac 1 2 left frac partial partial x mathrm i frac partial partial y right kismi diferansiyel operatorlerine Wirtinger turev operatorleri ya da sadece Wirtinger operatorleri denilir Wirtinger operatorlerinin tanim kumesi en dogal haliyle turevlenebilir fonksiyonlari icermektedir Ancak operatorler dogrusal olduklari ve sabit katsayilara sahip olduklari icin tanim kumeleri genellestirilmis fonksiyonlarin her turlu uzayina da genisletilebilir Karmasik koordinat uzayinda tanim Yukarida verilen ve bir karmasik degiskenli fonksiyonlar icin tanimlanan Wirtinger operatorlerinin tanimi yuksek boyutta tanimli ve karmasik degerler alan fonksiyonlar icin de verilebilir Cn R2n x y x1 xn y1 yn x y Rn displaystyle mathbb C n mathbb R 2n left left mathbf x mathbf y right left x 1 ldots x n y 1 ldots y n right mid mathbf x mathbf y in mathbb R n right alinirsa karmasik koordinat uzayindaki Wirtinger operatorleri her koordinatta ayri ayri tanimlanabilir z1 12 x1 i y1 zn 12 xn i yn z 1 12 x1 i y1 z n 12 xn i yn displaystyle begin cases frac partial partial z 1 frac 1 2 left frac partial partial x 1 i frac partial partial y 1 right qquad vdots frac partial partial z n frac 1 2 left frac partial partial x n i frac partial partial y n right end cases qquad begin cases frac partial partial bar z 1 frac 1 2 left frac partial partial x 1 i frac partial partial y 1 right qquad vdots frac partial partial bar z n frac 1 2 left frac partial partial x n i frac partial partial y n right end cases Daha once bahsedildigi uzere yine operatorler dogrusal olduklari ve sabit katsayilara sahip olduklari icin tanim kumeleri genellestirilmis fonksiyonlarin her turlu uzayina da genisletilebilir Karmasik turevlenebilme ile iliskisiBir fonksiyon bir noktada karmasik turevlenebilir ise fonksiyonun Wirtinger turevi Cauchy Riemann denklemleri sayesinde fonksiyonun karmasik turevine esittir Gercekten de eger bir f displaystyle f fonksiyonu karmasik turevlenebilirse o zaman Cauchy Riemann denklemleri bu fonksiyon icin saglanir yani fonksiyonun karmasik turevli oldugu acik kume uzerinde u x v y ve u y v x displaystyle frac partial u partial x frac partial v partial y text ve frac partial u partial y frac partial v partial x esitlikleri vardir Wirtinger turevinin tanimiyla baslayarak ve Cauchy Riemann denklemleri kullanarak f z 12 f x i f y 12 u x i v x i u y v y u z i v z dfdz displaystyle begin aligned frac partial f partial z amp frac 1 2 left frac partial f partial x i frac partial f partial y right amp frac 1 2 left frac partial u partial x i frac partial v partial x i frac partial u partial y frac partial v partial y right amp frac partial u partial z i frac partial v partial z frac df dz end aligned elde edilir Wirtinger turevinin karmasik eslenik degiskendeki hali de yine karmasik turevlenebilmeyle alakalidir f z 0 displaystyle frac partial f partial bar z 0 ifadesi aslinda Cauchy Riemann denklemlerinin karmasik halidir Cauchy Riemann operatoru f z displaystyle textstyle frac partial f partial z icin bazen kisaca f displaystyle partial f yazilir Yine benzer sekilde f z displaystyle textstyle frac partial f partial bar z icinse kisa bir sekilde f displaystyle bar partial f de yazilir displaystyle overline partial operatorune Cauchy Riemann operatoru denilir Aslinda bu kisaltma ifadeleri sadece fonksiyonlar icin gelistirilmis kisaltma gosterimleri degildir Daha dogrusu fonksiyonlarin 0 0 ikili derecesiyle ozel bir hali oldugu karmasik diferansiyel formlar icin tanimli turev operatoru d displaystyle d nin yukarida n 1 displaystyle n 1 hali icin df f zdz f z displaystyle df frac partial f partial z dz frac partial f partial bar z elde edildigi gibi d displaystyle d operatoru displaystyle partial ve displaystyle overline partial opeatorlerinin toplami olarak genel durumda da ayrisabilir Bunu gormek icin Cn displaystyle mathbb C n nin bir elemanini z1 zn x1 iy1 xn iyn displaystyle z 1 ldots z n x 1 mathrm i y 1 ldots x n mathrm i y n olarak yazalim D Cn displaystyle D subset mathbb C n acik bir kume olsun f f1 fm D Cm displaystyle f f 1 ldots f m D rightarrow mathbb C m ise gercel turevli bir gonderim olsun Yukarida verilen tanimlar araciligiyla f j 1n zjfdzj displaystyle partial f sum j 1 n frac partial partial z j f rm d z j ve f j 1n z jfdz j displaystyle overline partial f sum j 1 n frac partial partial overline z j f rm d overline z j tanimlanabilir O zaman df f f displaystyle mathrm d f overline partial f partial f elde edilir Holomorfluk durumunda df f displaystyle textstyle mathrm d f partial f elde edilir cunku bu durumda f 0 displaystyle overline partial f 0 olmaktadir cauchy Riemann operatorlerinin n gt 1 displaystyle n gt 1 icin yukaridaki gibi tanimlanmis hali dayanilarak Dolbeault operatorleri olarak da bilinir Yine de Cauchy Riemann opeatorleri ifadesi boyut sayisina isaret etmeksizin kullanilabilir OzelliklerAsagida verilen ozelliklerde n 1 displaystyle n geq 1 olmak uzere z Cn displaystyle z in mathbb C n karmasik vektor ve x y displaystyle x y gercel vektorler olmak uzere z x y x1 xn y1 yn displaystyle z equiv x y x 1 ldots x n y 1 ldots y n olsun Ayrica W displaystyle Omega R2n displaystyle mathbb R 2n de ya da bu uzayin izomorf oldugu Cn displaystyle mathbb C n de acik bir kume olsun Dogrusallik f g C1 W displaystyle f g in C 1 Omega ve a b displaystyle alpha beta karmasik sayi olsun O zaman her i 1 n displaystyle i 1 dots n icin asagidaki esitlikler saglanir zi af bg a f zi b g zi z i af bg a f z i b g z i displaystyle begin aligned frac partial partial z i left alpha f beta g right amp alpha frac partial f partial z i beta frac partial g partial z i frac partial partial bar z i left alpha f beta g right amp alpha frac partial f partial bar z i beta frac partial g partial bar z i end aligned Carpma kurali f g C1 W displaystyle f g in C 1 Omega ve a b displaystyle alpha beta karmasik sayi olsun O zaman her i 1 n displaystyle i 1 dots n icin carpma kurali saglanir zi f g f zi g f g zi z i f g f z i g f g z i displaystyle begin aligned frac partial partial z i f cdot g amp frac partial f partial z i cdot g f cdot frac partial g partial z i frac partial partial bar z i f cdot g amp frac partial f partial bar z i cdot g f cdot frac partial g partial bar z i end aligned Zincir kurali Zincir kuralinin iki hali icin W Cm displaystyle Omega subseteq mathbb C m ve W Cp displaystyle Omega subseteq mathbb C p olmak uzere bmlgeler ele alalim g W W displaystyle g Omega to Omega ve f W W displaystyle f Omega to Omega ise bu bolgeler arasinda belirli turevlilik sartlarini yeteri kadar saglayan gonderim olsunlar Bir karmasik degiskenli fonksiyonlar icin zincir kurali f g C1 W displaystyle f g in C 1 Omega ve g W W displaystyle g Omega subseteq Omega ise o zaman zincir kuralinin asagidaki bicimleri saglanir z f g f z g g z f z g g z z f g f z g g z f z g g z displaystyle begin aligned frac partial partial z f circ g amp left frac partial f partial z circ g right frac partial g partial z left frac partial f partial bar z circ g right frac partial bar g partial z frac partial partial bar z f circ g amp left frac partial f partial z circ g right frac partial g partial bar z left frac partial f partial bar z circ g right frac partial bar g partial bar z end aligned n gt 1 karmasik degiskenli fonksiyonlar icin zincir kurali g C1 W W displaystyle g in C 1 Omega Omega ve f C1 W W displaystyle f in C 1 Omega Omega olsun Her i 1 m displaystyle i 1 dots m icin zincir kuralinin asagidaki bicimleri saglanir zi f g j 1n f zj g gj zi j 1n f z j g g j zi z i f g j 1n f zj g gj z i j 1n f z j g g j z i displaystyle begin aligned frac partial partial z i left f circ g right amp sum j 1 n left frac partial f partial z j circ g right frac partial g j partial z i sum j 1 n left frac partial f partial bar z j circ g right frac partial bar g j partial z i frac partial partial bar z i left f circ g right amp sum j 1 n left frac partial f partial z j circ g right frac partial g j partial bar z i sum j 1 n left frac partial f partial bar z j circ g right frac partial bar g j partial bar z i end aligned Eslenik alma altina Wirtinger operatorleri f C1 W displaystyle f in C 1 Omega ise i 1 n displaystyle i 1 dots n icin asagidaki esitlikler saglanir f zi f z i f z i f zi displaystyle begin aligned overline left frac partial f partial z i right amp frac partial bar f partial bar z i overline left frac partial f partial bar z i right amp frac partial bar f partial z i end aligned Notlar ve kaynakca 1986 Unification of global and local existence theorems for holomorphic functions of several complex variables Memorie della Accademia Nazionale dei Lincei Classe di Scienze Fisiche Matematiche e Naturali 8 18 3 ss 61 83 MR 0917525 Zbl 0705 32006 Kracht Manfred 1988 Methods of Complex Analysis in Partial Differential Equations and Applications Series of Monographs and Advanced Texts New York Chichester Brisbane Toronto Singapore John Wiley amp Sons ss xiv 394 ISBN 0 471 83091 7 MR 0941372 Zbl 0644 35005 Wirtinger Wilhelm 1927 Zur formalen Theorie der Funktionen von mehr komplexen Veranderlichen Birkac karmasik degiskenli fonksiyonlarin formel teorisi uzerine Almanca 97 1 ss 357 375 doi 10 1007 BF01447872 JFM 52 0342 03 Poincare 1899 ss 111 114 e bakiniz Bu fonksiyonlar aslinda bugun cokluharmonik denilen fonksiyonlardir 1969 Derivata areolare e funzioni a variazione limitata Italyanca XIV 1 ss 27 37 MR 0265616 Zbl 0201 10002 Levi Eugenio Elia 1910 Studii sui punti singolari essenziali delle funzioni analitiche di due o piu variabili complesse s III Italyanca XVII 1 ss 61 87 doi 10 1007 BF02419336 JFM 41 0487 01 Levi Eugenio Elia 1911 Sulle ipersuperficie dello spazio a 4 dimensioni che possono essere frontiera del campo di esistenza di una funzione analitica di due variabili complesse s III Italyanca XVIII 1 ss 69 79 doi 10 1007 BF02420535 JFM 42 0449 02 1905 Sulle funzioni di due o piu variabili complesse Rendiconti della Accademia Nazionale dei Lincei Classe di Scienze Fisiche Matematiche e Naturali 5 Italyanca XIV 2 ss 492 499 JFM 36 0482 01 Osgood William Fogg 1966 1913 Topics in the theory of functions of several complex variables unabridged and corrected bas New York Dover ss IV 120 JFM 45 0661 02 MR 0201668 Zbl 0138 30901 1993 1986 Applied and Computational Complex Analysis Volume 3 Wiley Classics Library Reprint bas New York Chichester Brisbane Toronto Singapore John Wiley amp Sons ss X 637 ISBN 0 471 58986 1 MR 0822470 Zbl 1107 30300 Poincare H 1899 Sur les proprietes du potentiel et sur les fonctions Abeliennes Fransizca 22 1 ss 89 178 doi 10 1007 BF02417872 JFM 29 0370 02 1912 Sur une classe de fonctions d une variable complexe Fransizca 33 1 ss 108 113 doi 10 1007 BF03015292 JFM 43 0481 01 1913 Sur une classe de fonctions d une variable complexe et sur certaines equations integrales Fransizca 35 1 ss 277 281 doi 10 1007 BF03015607 Vekua I N 1962 Generalized Analytic Functions International Series of Monographs in Pure and Applied Mathematics 25 London Paris Frankfurt Pergamon Press ss xxx 668 MR 0150320 Zbl 0100 07603 Ayrica bakiniz
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans

























