Matematikte Jensen eşitsizliği dışbükey ve içbükey fonksiyonlar için temel bir eşitsizliktir. Eşitsizliğin birkaç değişik biçimi vardır; özellikle, analizde ve bilgi teorisinde başka birçok eşitsizliğin de temelini oluşturmaktadır.

Eşitsizlik, adını 17 Ocak 1905'te Danimarka Matematik Derneği'nin bir konferansında sunan Danimarkalı matematikçi ve mühendis Johan Ludwig Jensen'den almıştır. Biraz farklı koşullar altında sunulmuş ve Otto Hölder tarafından 1889 yılında kanıtlanmış bir hâli de bulunabilir.
Jensen eşitsizliği, bir dışbükey fonksiyonun sonlu sayıdaki noktalardan oluşan bir dışbükey katışım (kombinasyon) noktasında aldığı değerin, fonksiyonun bu sonlu noktadaki aldığı değerlerinin sonlu dışbükey katışımından küçük veya eşit olduğunu belirtir. Eşitlik her zaman doğrusal fonksiyonlar için geçerlidir. Özellikle, Jensen eşitsizliği, bir dışbükey fonksiyonun kesen doğrusunun fonksiyonun grafiğinin üstünde yer aldığı ifadesini genelleştirir. Başka bir deyişle, Jensen iki nokta için kullanıldığında, fonksiyonun grafiğinin iki noktasını kesen doğru (t ∈ [0,1] için),
olurken, fonksiyonun grafiğinin bu noktalar arasındaki kısmı ise
tarafından verilir. Sonuç olarak, Jensen eşitsizliği
halini alır.
Eşitsizliğin değişik biçimdeki ifadeleri
Sonlu biçimi
Gerçel değerli bir 


olur. Eğer fonksiyon içbükeyse, eşitsizlik yönü değişir ve
olur. Eşitlik, ancak ve ancak 

Aritmetik ortalama-geometrik ortalama eşitsizliği
Eğer 
ve
olurlar. Dahası, fonksiyonu 


Ölçü kuramındaki biçimi







ifadesinin kestirimi lazım olur. Elbette, bu durumda, 
Olasılıktaki biçimi


Olasılık durumunda, μ ölçüsünün yerine 
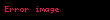




Kanıtlar
Sonlu biçim için kanıt
Sonlu biçimdeki Jensen eşitliğinin kanıtı tümevarımla verilebilir. Fonksiyonun dışbğkeyliğinden başlangıç adımı 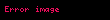

doğru olsun. Eşitsizliği, n + 1 için kanıtlamamız gerekecek. Bu durumda, λ1 + ... +λn + λn+1 = 1 olduğu içn, en azından bir tane λi 
yazabiliriz. λn+1 
yazılabilir. O hâlde, tümevarım varsayım adımını kullanarak,
elde ederiz. Bu yüzden,
olur.
Ölçü kuramsal biçim için kanıt









tanımlarsak, dışbükey fonksiyonların altürevlerinin varlığı sayesinde, öyle bir 

eşitliği tüm 
olur ve o zaman, hemen hemen tüm 
olur. Olasılık ölçüsünde olduğumuz için, integralin de artma özelliği vardır (
elde edilir.
Kaynakça
- ^ Johan Ludwig William Valdemar Jensen (1906), "Sur les fonctions convexes et les inégalités entre les valeurs moyennes", Acta Math., cilt 30, ss. 175-193, doi:10.1007/BF02418571
- ^ Otto Hölder (1889), "Ueber einen Mittelwerthssatz", Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen, Göttingen: Dieterichsche Verlags-Buchhandlung, 1889 (1-21), s. 38
- ^ p. 25 of (2019). Probability: Theory and Examples. 5th. Cambridge University Press. ISBN . 12 Haziran 2024 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Aralık 2024.
- ^ Niculescu, Constantin P. "Integral inequalities" 6 Mayıs 2021 tarihinde Wayback Machine sitesinde arşivlendi., S. 12.
- ^ p. 29 of (2019). Probability: Theory and Examples. 5th. Cambridge University Press. ISBN . 12 Haziran 2024 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Aralık 2024.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Jensen esitsizligi disbukey ve icbukey fonksiyonlar icin temel bir esitsizliktir Esitsizligin birkac degisik bicimi vardir ozellikle analizde ve bilgi teorisinde baska bircok esitsizligin de temelini olusturmaktadir Jensen esitsiligi disbukey bir fonksiyonun kesen dogrusunun grafigin uzerinde kaldigi ifadesini genellestirir Esitsizlik adini 17 Ocak 1905 te Danimarka Matematik Dernegi nin bir konferansinda sunan Danimarkali matematikci ve muhendis Johan Ludwig Jensen den almistir Biraz farkli kosullar altinda sunulmus ve Otto Holder tarafindan 1889 yilinda kanitlanmis bir hali de bulunabilir Jensen esitsizligi bir disbukey fonksiyonun sonlu sayidaki noktalardan olusan bir disbukey katisim kombinasyon noktasinda aldigi degerin fonksiyonun bu sonlu noktadaki aldigi degerlerinin sonlu disbukey katisimindan kucuk veya esit oldugunu belirtir Esitlik her zaman dogrusal fonksiyonlar icin gecerlidir Ozellikle Jensen esitsizligi bir disbukey fonksiyonun kesen dogrusunun fonksiyonun grafiginin ustunde yer aldigi ifadesini genellestirir Baska bir deyisle Jensen iki nokta icin kullanildiginda fonksiyonun grafiginin iki noktasini kesen dogru t 0 1 icin tf x1 1 t f x2 displaystyle tf x 1 1 t f x 2 olurken fonksiyonun grafiginin bu noktalar arasindaki kismi ise f tx1 1 t x2 displaystyle f tx 1 1 t x 2 tarafindan verilir Sonuc olarak Jensen esitsizligi f tx1 1 t x2 tf x1 1 t f x2 displaystyle f tx 1 1 t x 2 leq tf x 1 1 t f x 2 halini alir Esitsizligin degisik bicimdeki ifadeleriSonlu bicimi Gercel degerli bir f displaystyle varphi fonksiyonu ve bu fonksiyonun tanim kumesinde x1 x2 xn displaystyle x 1 x 2 ldots x n noktalari olsun Toplamlari 1 olan pozitif ai displaystyle a i sayilari icin f i 1naixi i 1naif xi displaystyle varphi left sum i 1 n a i x i right leq sum i 1 n a i varphi x i olur Eger fonksiyon icbukeyse esitsizlik yonu degisir ve f i 1naixi i 1naif xi displaystyle varphi left sum i 1 n a i x i right geq sum i 1 n a i varphi x i olur Esitlik ancak ve ancak x1 x2 xn displaystyle x 1 x 2 cdots x n olursa ya da f displaystyle varphi dogrusal bir fonksiyonsa gerceklesir Aritmetik ortalama geometrik ortalama esitsizligi Eger ai 1n displaystyle a i frac 1 n alinirsa o zaman yukaridaki esitsizlikler f xin f xi n displaystyle varphi left frac sum x i n right leq frac sum varphi x i n ve f xin f xi n displaystyle varphi left frac sum x i n right geq frac sum varphi x i n olurlar Dahasi fonksiyonu f x log x displaystyle f x log x alirsak o zaman bu fonksiyon icbukey oldugu icin log i 1nxin i 1nlog xi n displaystyle log left frac sum i 1 n x i n right geq frac sum i 1 n log left x i right n elde edilir Her iki tarafin ilk once ustelini alip daha sonra ustel fonksiyon ile logaritmanin birbirlerinin tersi oldugunu ve bu fonksiyonlarin ozelliklerini kullanarak x1 x2 xnn x1 x2 xnn displaystyle frac x 1 x 2 cdots x n n geq sqrt n x 1 cdot x 2 cdots x n elde ederiz Olcu kuramindaki bicimi W A m displaystyle Omega A mu bir olasilik uzayi olsun f W R displaystyle f Omega to mathbb R fonksiyonu m displaystyle mu olculebilir olsun ve f R R displaystyle varphi mathbb R to mathbb R diisbukey bir fonksiyon olsun O zaman f Wfdm Wf fdm displaystyle varphi left int Omega f mathrm d mu right leq int Omega varphi circ f mathrm d mu olur Gercel analizde bazen negatif olmayab ve Lebesgue integrali var olan bir f a b R displaystyle f colon a b to mathbb R fonksiyonu ve belli bir a b R displaystyle a b in mathbb R sayilari icin f abf x dx displaystyle varphi left int a b f x dx right ifadesinin kestirimi lazim olur Elbette bu durumda a b displaystyle a b araliginin uzunlugu 1 olmayabilir Bu durumda integralde yerine koyma yontemiyle bu araligi olceklendirip esitsizligin kullanimina uygun hale getirebiliriz f 1b a abf x dx 1b a abf f x dx displaystyle varphi left frac 1 b a int a b f x dx right leq frac 1 b a int a b varphi f x dx Olasiliktaki bicimi W F P displaystyle Omega mathfrak F operatorname P olasilik uzayi X gercel degerli ve integrallenebilir bir rasgele degisken ve f displaystyle varphi disbukey bir fonksiyon olsun O zaman f E X E f X displaystyle varphi left operatorname E X right leq operatorname E left varphi X right Olasilik durumunda m olcusunun yerine P displaystyle operatorname P olasiligi m ye gore olan integralin yerine E displaystyle operatorname E yani beklenen deger ve son olarak foknsiyon f displaystyle f yerine de X rasgele degiskeni gelmistir Son olarak esitlik ancak ve ancak f displaystyle varphi P X A 1 displaystyle mathrm P X in A 1 ozelligini saglayan disbukey bir A displaystyle A kumesi uzerinde dogrusal olursa saglanir KanitlarSonlu bicim icin kanit Sonlu bicimdeki Jensen esitliginin kaniti tumevarimla verilebilir Fonksiyonun disbgkeyliginden baslangic adimi n 2 displaystyle n 2 icin dogrudur Diyelim ki tumevarimdaki varsayim geregi bir n displaystyle n sayisi icin esitsilik dogru olsun Yani her x1 xn icin ve l1 ln 1 olan her l1 ln icin f i 1nlixi i 1nlif xi displaystyle varphi left sum i 1 n lambda i x i right leq sum i 1 n lambda i varphi left x i right dogru olsun Esitsizligi n 1 icin kanitlamamiz gerekecek Bu durumda l1 ln ln 1 1 oldugu icn en azindan bir tane li 1 displaystyle 1 den kesin kucuk olacak Diyelim ki ln 1 olsun Disbukey esitsizliginden f i 1n 1lixi f 1 ln 1 i 1nli1 ln 1xi ln 1xn 1 1 ln 1 f i 1nli1 ln 1xi ln 1f xn 1 displaystyle begin aligned varphi left sum i 1 n 1 lambda i x i right amp varphi left 1 lambda n 1 sum i 1 n frac lambda i 1 lambda n 1 x i lambda n 1 x n 1 right amp leq 1 lambda n 1 varphi left sum i 1 n frac lambda i 1 lambda n 1 x i right lambda n 1 varphi x n 1 end aligned yazabiliriz ln 1 1 displaystyle 1 den kesin kucuk oldugu icin i 1nli1 ln 1 1 displaystyle sum i 1 n frac lambda i 1 lambda n 1 1 yazilabilir O halde tumevarim varsayim adimini kullanarak f i 1nli1 ln 1xi i 1nli1 ln 1f xi displaystyle varphi left sum i 1 n frac lambda i 1 lambda n 1 x i right leq sum i 1 n frac lambda i 1 lambda n 1 varphi x i elde ederiz Bu yuzden f i 1n 1lixi 1 ln 1 i 1nli1 ln 1f xi ln 1f xn 1 i 1n 1lif xi displaystyle begin aligned varphi left sum i 1 n 1 lambda i x i right amp leq 1 lambda n 1 sum i 1 n frac lambda i 1 lambda n 1 varphi x i lambda n 1 varphi x n 1 sum i 1 n 1 lambda i varphi x i end aligned olur Olcu kuramsal bicim icin kanit W A m displaystyle Omega A mu bir olasilik uzayi olsun f W R displaystyle f Omega to mathbb R fonksiyonu m displaystyle mu olculebilir olsun ve f R R displaystyle varphi mathbb R to mathbb R disbukey bir fonksiyon olsun f displaystyle varphi disbukey oldugu icin her gercel x displaystyle x sayisi icin bos olmayan bir altturev kumesi vardir Burada altturev kumesi f displaystyle varphi nin grafigine x displaystyle x noktasinda dokunan ama f displaystyle varphi nin grafiginin altinda kalan dogrular olarak dusunulebilir Simdi x0 Wgdm displaystyle x 0 int Omega g d mu tanimlarsak disbukey fonksiyonlarin alturevlerinin varligi sayesinde oyle bir a displaystyle a ve b displaystyle b secebiliriz ki ax b f x displaystyle ax b leq varphi x esitligi tum x displaystyle x degerleri icin saglanir Sonuc olarak ax0 b f x0 displaystyle ax 0 b varphi x 0 olur ve o zaman hemen hemen tum w W displaystyle omega in Omega icin f g w ag w b displaystyle varphi circ g omega geq ag omega b olur Olasilik olcusunde oldugumuz icin integralin de artma ozelligi vardir m W 1 displaystyle mu Omega 1 Boylece Wf gdm W ag b dm a Wgdm b Wdm ax0 b f x0 f Wgdm displaystyle int Omega varphi circ g d mu geq int Omega ag b d mu a int Omega g d mu b int Omega d mu ax 0 b varphi x 0 varphi left int Omega g d mu right elde edilir Kaynakca Johan Ludwig William Valdemar Jensen 1906 Sur les fonctions convexes et les inegalites entre les valeurs moyennes Acta Math cilt 30 ss 175 193 doi 10 1007 BF02418571 Otto Holder 1889 Ueber einen Mittelwerthssatz Nachrichten von der Konigl Gesellschaft der Wissenschaften und der Georg Augusts Universitat zu Gottingen Gottingen Dieterichsche Verlags Buchhandlung 1889 1 21 s 38 p 25 of 2019 Probability Theory and Examples 5th Cambridge University Press ISBN 978 1108473682 12 Haziran 2024 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Aralik 2024 Niculescu Constantin P Integral inequalities 6 Mayis 2021 tarihinde Wayback Machine sitesinde arsivlendi S 12 p 29 of 2019 Probability Theory and Examples 5th Cambridge University Press ISBN 978 1108473682 12 Haziran 2024 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Aralik 2024
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans



















