Matematiksel Mantık

Matematiksel mantık biçimsel mantığın matematiğe uygulanmasıyla ilgilenen bir matematik dalıdır. , matematiğin temelleri ve kuramsal bilgisayar bilimi alanlarıyla yakınlık gösterir. Matematiksel mantığın temel konuları ifade gücünün ve biçimsel ispat sistemlerinin tümdengelim gücünün belirlenmesidir.

Matematiksel mantık kümeler kuramı, model kuramı, hesaplanabilirlik kuramı ve tanıtlama kuramı alanlarına ayrılır. Bu alanlar mantığın, özellikle ve konularındaki, temel sonuçlarını paylaşır.

Tarihçe

Çağdaş mantığın ve çağdaş felsefenin kurucusu Alman mantıkçısı Gottlob Frege, "Matematik mantığın uygulama alanıdır." görüşünden hareketle matematiğin, mantığın aksiyomatik sistemi üzerine kurulabileceğini düşünmüştür. Bu düşünceden hareket ederek aritmetiğin temelleri konusundaki felsefi çalışmaları için bir mantık sistemi geliştirmişti.

Daha sonra, Frege'nin çalışmalarına dayanarak, Bertrand Russell ve Alfred North Whitehead 1910-1913 yılları arasında Principia Mathematica adını verdikleri eserde matematiği mantığa indirgeyerek formel bir sistem haline getirmeye çalıştılar. Fakat matematiğin formel hale getirilemeyeceğini Kurt Gödel 1933'te yayınladığı bir kitabındaki (Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme) meşhur teoremiyle gösterdi.

John Alan Robinson, 1967'de çözülüm teorem ispatlama yöntemini geliştirdi. Bu yöntem 1972'de A. Colmaurer tarafından ilk mantık programlama dilinin (Prolog) geliştirilmesine yol açtı. Bu dil 1975'te D. Warren tarafından “Warren Abstract Machine” (WAM) olarak uygulandı. Kişisel bilgisayarlar üzerinde ilk uygulamalar 1980'lerde ortaya çıktı.

Önermeler Mantığı

Formel sistemler şu elemanlardan meydana gelir:

1. Tanımlanmamış terimler
2. Tanımlar
3. Türetme kuralları
4. Aksiyomlar
5. Teoremler

Formel mantığın tanımlanmamış terimleri olarak, basit önerme (P) ve mantık bağlaçları (değil, ve, veya, eğer-ise, eğer ve ancak-ise) gösterilebilir.

Tanımlanan terimlere örnek olarak bileşik önerme kavramını gösterilebilir. Aslında yukarıda verilen mantıksal bağlaçlar bir tek mantıksal bağlaç yardımıyla tanımlanabilir.

Önerme

Doğru ya da yanlış kesin hüküm bildiren ifadelere önerme denir. Bir önerme hem doğru hem de yanlış olamaz ama bazı önermelerin doğruluk değerleri (Doğru önermelerin doğruluk değeri 1, Yanlış önermelerin doğruluk değeri 0'dır) değişebilir. Mesela "Dün hava yağmurluydu" önermesinin doğruluk değeri günden güne değişebilir ama her önermenin doğruluk değeri değişmez "1+1=2" önermesi her zaman doğrudur. Aşağıdaki cümleler önermelere örnektir:

Dün hava güneşliydi. 3 asal sayıdır.

Duygu 21 yaşındadır.

3 asal sayı değildir.

Derya 21 yaşında değildir.

Bir gün 24 saattir.

Sıfır doğal sayıdır.

Mantıksal bağlaçlar kullanarak basit önermelerden başka önermeler kurulabilir, ki bunlara “bileşik önermeler” denir. Önerme matematikte kesin bir hüküm bildiren ifadelere denir.

Olumsuzu

Bir önerme “değil” eki ile karşıt ifadeye çevrilebilir; buna olumsuzunu alma denir.

Bir hafta 7 gün'dür. Bir hafta 7 gün değildir. Olumsuz olacak harfin önüne - ifadesi eklenir.

Birleşim

İki veya daha fazla önermeden "ve, veya, ise" mantıksal bağlaçlarını kullanarak bileşik önermeler kurulabilir. Örnek olarak: “Bugün hava açık ve sıcak” cümlesini verebilir. Doğal dilde bazen “fakat” bağlacını da kullanıyoruz.

'Örnek': “bugün gemiler 9'da veya 10'da sefer yapacak.”

“arkadaşlarım sınıftadır veya arkadaşlarım bahçededir.”

değili A' olarak gösterilir.

Ayrılım

İki veya daha fazla basit önermeden “veya” (ya da) mantıksal bağını kullanarak bileşik önermeler kurulabilir.

Örnek: “Bugün Arçelik veya Tedaş'tan ziyaretçiler gelecek.”

Şartlı cümle

Aynı şekilde, iki veya daha fazla sayıda önermeden (eğer-ise) bağını kullanarak şartlı önermeler kurulabilir.

Örnek: “Eğer yağmur yağıyor ise, hava bulutludur.”

Bazen “eğer-ise” bağı yerine doğal dilde “gerektirir” bağını da kullanabiliyoruz.

Örnek: “Yağmurun yağıyor olması havanın bulutlu olmasını gerektirir.”

Ancak ve ancak

Yine, “eğer ve ancak-ise” bağını kullanarak birden fazla önermeden çift şartlı önermeler kurulabilir. Bu tür önermeler doğal dilde daha az kullanılmasına rağmen, fizik ve matematikte sık sık kullanılmaktadır.

Örnek: “Eğer ve ancak çalışanlar ücretlerde aşırı artış talep ederlerse enflasyon düşmez.”

Aynı cümle şu şekilde de ifade edilebilir: “Eğer, çalışanlar ücretlerde aşırı artış talep ederlerse enflasyon düşmez ve eğer enflasyon düşmezse çalışanlar ücretlerde aşırı artış talep ederler.”

Cebirde olduğu gibi, sembolik veya matematiksel mantıkta da, önermeler yerine önermesel değişkenler kullanılır (P, Q, R, S, T harfleri gibi).

Mantıksal Bağlaçlar

Mantıksal bağlaçlar aşağıdaki sembollerle gösterilir:

${\displaystyle \neg }$: değil
${\displaystyle \land }$: ve
${\displaystyle \lor }$: veya
${\displaystyle \to }$: eğer-ise
${\displaystyle \leftrightarrow }$: ancak ve ancak

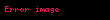
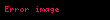
Böylece şu ifadeler, önerme formülleri olacaktır:

${\displaystyle \neg P}$, ${\displaystyle P\land Q}$, ${\displaystyle P\lor Q}$, ${\displaystyle P\to Q}$, ${\displaystyle P\leftrightarrow Q}$

---

Örnek: "Eğer sendika veya fabrika yöneticileri inada devam ederlerse, grev ancak ve ancak hükûmet bir kararname çıkarır ve fabrikaya polis göndermezse önlenir."

P: Sendika inada devam eder
Q: Fabrika yöneticileri inada devam eder
R: Grev önlenir
S: Hükûmet kararname çıkartır
T: Hükûmet fabrikaya polis göndermez

${\displaystyle (P\lor Q)\to (R\leftrightarrow S\land T)}$

---

=> ise bu şekilde de gösterilir <=> ancak ve ancak bu şekilde de gösterilir.

Doğruluk cetvelleri

Mantıkta önermeler doğru ya da yanlış olabilir, fakat hem doğru hem yanlış olamaz. Bir önermeye yüklenen bu doğru ve yanlış yüklemlerine onun doğruluk değeri denir.

${\displaystyle \neg P}$, ${\displaystyle P\land Q}$, ${\displaystyle P\lor Q}$, ${\displaystyle P\to Q}$, ${\displaystyle P\leftrightarrow Q}$

“Değil” sözcüğünün anlamından hareketle, eğer bir P önermesi doğru ise onun değillemesi, yani ${\displaystyle \neg P}$ yanlıştır ve bunun tersi. Mesela, P önermesi “Ay dünyanın uydusudur” cümlesi yerine geçiyorsa, bunun değillemesi olan ${\displaystyle \neg P}$ yanlıştır.

Genel, kural olarak iki veya daha fazla önermenin birleşimi, ancak birleşen bütün önermelerin doğru olması halinde doğrudur. Mesela, “3 asal sayıdır ve 2+2=5'tir” yanlış bir bileşik önermedir.

Yine kural olarak, ayrık önermelerin doğru olabilmesi için bileşenlerden birinin doğru olması yeterlidir. Ayrık önermeler ancak bunları meydana getiren bileşenlerin hepsinin birden yanlış olduğu halde yanlış sayılır.

Bileşik önermeler için doğruluk tabloları şu şekilde verilebilir:

${\displaystyle P}$	${\displaystyle Q}$	${\displaystyle \neg P}$	${\displaystyle P\land Q}$	${\displaystyle P\lor Q}$	${\displaystyle P\to Q}$	${\displaystyle P\leftrightarrow Q}$
D	D	Y	D	D	D	D
D	Y	Y	Y	D	Y	Y
Y	D	D	Y	D	D	Y
Y	Y	D	Y	Y	D	D

D: doğru, Y: yanlış

Eşdeğerlikler

${\displaystyle \neg \neg P=P}$
${\displaystyle \neg P\lor Q=P\to Q}$
${\displaystyle \neg (P\lor Q)=\neg P\land \neg Q}$
${\displaystyle \neg (P\land Q)=\neg P\lor \neg Q}$

${\displaystyle (P\Leftrightarrow Q)=(P\Rightarrow Q)\land (Q\Rightarrow P)}$

Karşıtlıklar

${\displaystyle \neg P\times P}$
${\displaystyle (P\to Q)\times (P\land \neg Q)}$
${\displaystyle (P\lor Q)\times (\neg P\land \neg Q)}$
${\displaystyle (P\land Q)\times (\neg P\lor \neg Q)}$

Totoloji

Bir önermesel formülün (veya bileşik önermenin) doğruluk cetvelindeki son değerlendirme sütunundaki bütün değerler “doğru” çıkıyorsa, bu önermesel formüle “totoloji” denir.

Çelişki

Bir önermesel formülün (veya bileşik önermenin) doğruluk cetvelindeki son değerlendirme sütunundaki bütün değerler “yanlış” çıkıyorsa bu önermesel formüle “çelişki” denir.

Bazen doğruluk

Bir önermesel formülün (veya bileşik önermenin) doğruluk cetvelindeki son değerlendirme sütunundaki değerlerden bazıları “doğru” bazıları “yanlış” çıkıyorsa bu önermesel formüle “bazen doğru” denir.

Tutarlılık

Bir bileşik önermeye “ve” ekiyle başka bir önerme eklendiği zaman bir çelişki ortaya çıkmıyorsa, eklenen önerme öncekiyle tutarlıdır denir.

Geçerlilik

Bir A₁, A₂, ..., A_n önerme dizisindeki bütün A’lar doğru olduğu zaman bir B hükmü de doğru oluyorsa B’ye A₁, A₂, ..., A_n önermelerinin geçerli sonucudur denir. Geçerlilik şu şekilde gösterilir:

A₁, A₂, ..., A_n |= B.

Mantıksal İçerik

Bir bileşik önermeyi yanlış yapan şartların sayısının bütün şartların sayısına oranı ne kadar büyükse, o önermenin mantıksal içeriği o kadar fazladır. Çelişkinin mantıksal içeriğinden bahsedilemez (çünkü yoktur.).(-->bu durumda çelişki için mantıksal içerik 1/1 olması beklenir. buna göre ilk cümle ile bahsedilen tanım tersi olarak düşünülmesi gerekmektedir =>düzeltmedir, şayet hata yok ise siliniz?)

Yüklemler Mantığı

Önermeler mantığının türetim kuralları matematik için yeterli olmadığı gibi gündelik dil için de yeterli değildir. Mesela, klasik mantıkta "Her asal sayı bir doğal sayıdır" ve "3 asal sayıdır" öncüllerinden, "3 doğal sayıdır" sonucunu çıkarabiliyoruz. Fakat bu akıl yürütmenin doğruluğu, önermeler mantığının kuralları çerçevesi içinde kanıtlanamaz. Bunun nedeni de şudur: Önermeler mantığı bileşik önermeler içindeki basit önermeler arasındaki mantıksal bağlaçlara ve basit önermelerin doğruluk değerlerine göre bileşik önermelerin doğruluklarını inceler. Diğer bir deyişle, önermeler mantığı bir önermeyi birçok maksat için yeterli ayrıntıda analiz etmez.

İşte, terimler, yüklemler ve niceleyiciler diye isimlendireceğimiz mantıksal kavramlar yardımıyla gündelik dili ve matematiğin dilini büyük ölçüde sembolize edebiliriz.

Yüklemler mantığında da aynı matematikte olduğu gibi, sabitler ve değişkenler kullanılır. Biraz önce bahsedilen "terimleri" iki sınıfa ayırabiliriz: Bireysel değişkenler, bireysel sabitler. Bireysel sabitlere örnek olarak birey olduğunu bildiğimiz varlıkları sayabiliriz: “Gökhan”, “Tekir”, “gül” gibi. Bunlar yerine de “insan”, “hayvan”, “bitki” kavramlarının çerçeveleri içinde olmak üzere x, y, z, değişken sembollerini kullanabiliyoruz.

Matematikte değişkenler genellikle sayılar veya fonksiyonlar olabilir. Yüklemler mantığında ise bireysel terimler değişken olabildiği gibi, yüklemler de sabit veya değişken olabilir. Yüklemsel sabitlere örnek olarak önermeler içinde yer alan yüklemleri gösterebiliriz: “sayı”, “meyve”, “uydu”, “sert” gibi. Buna göre,

7 bir asal sayıdır.
Elma bir tür meyvedir.
Miranda, Neptün'ün uydusudur.
Demir sert bir metaldir.

...cümleleri içinde "7", "Elma", "Miranda", "Neptün" ve "demir" bireysel sabitler, “asal sayı, “meyve”, “uydu” ve “sert metal” de yüklemsel sabitlerdir.

Yüklemsel ifadelerde yüklemler yukarıdaki örneklerde görüldüğü gibi bir veya iki terimli (veya argümanlı) olabildiği gibi, daha fazla sayıda argüman da içerebilirler. Mesela: “Beril, Akın ve Şebnem'nin önünde oturuyor” dediğimiz zaman, burada “önünde oturuyor” ifadesini yüklem olarak; Beril, Akın ve Şebnem isimlerini de bireysel sabitler olarak almış oluyoruz.

Yüklemsel ifadeler yüklemin aldığı terim sayısına göre şu genel biçimlerde gösterilebilirler:

P(a), Q(b,c), R(d,e,f), ...

Bu ifadelerde, hemen görülebileceği gibi, bireysel sabitler yerine x, y, z gibi değişkenler koyarsak,

P(x), Q(b,y), R(z,e,f)

...gibi değişken terimli yüklemsel ifadeler elde ederiz.

Eşdeğerlik ve karşıtlık

A(x) yüklemsel bir formül olsun. Şu ifadeleri göz önüne alalım:

a) ${\displaystyle \forall xA(x)}$
b) ${\displaystyle \exists xA(x)}$
c) ${\displaystyle \forall x(\neg A(x))}$
d) ${\displaystyle \exists x(\neg A(x))}$

Bunları doğal dile çevirirsek:

a) Her şey A yüklemine (özelliğine) sahiptir.
b) Bazı şeyler A yüklemine (özelliğine) sahiptir.
c) Hiçbir şey A yüklemine (özelliğine) sahip değildir.
d) Bazı şeyler A yüklemine (özelliğine) sahip değildir.

Burada görüldüğü gibi, d, a'nın karşıtı (değillemesi), c de b'nin karşıtıdır. Şu halde, ${\displaystyle \exists xA(x)}$ yerine ${\displaystyle \neg \forall x\neg A(x)}$ kullanabiliriz, çünkü bunlar mantıksal olarak özdeştir, aynı şekilde ${\displaystyle \forall xA(x)}$ yerine ${\displaystyle \neg \exists x\neg A(x)}$ ifadesini kullanabiliriz.

Yüklemsel ifadelerde değilleme ve niceleyicilerin yeri, anlam bakımından önemlidir. Örneğin:

${\displaystyle \neg \forall xasal(x)}$, “her sayı asal değildir” anlamına gelirken,
${\displaystyle \forall x\neg asal(x)}$ ise “hiçbir sayı asal değildir” anlamına gelir.

Eşdeğerlikler

${\displaystyle \forall xP(x)=\neg [\exists x\neg P(x)]}$
${\displaystyle \exists xP(x)=\neg [\forall x\neg P(x)]}$
${\displaystyle \neg \exists xP(x)=\forall x\neg P(x)}$
${\displaystyle \neg \forall xP(x)=\exists x\neg P(x)}$

Karşıtlıklar

${\displaystyle \forall xP(x)\times \exists x\neg P(x)}$
${\displaystyle \exists xP(x)\times \forall x\neg P(x)}$
${\displaystyle \neg \exists xP(x)\times \exists xP(x)}$
${\displaystyle \neg \forall xP(x)\times \forall xP(x)}$

Çok Çözülüm Teorem İspatlama

Çözülüm teorem ispatlama, mantık teoremlerinin ispatlanması için A. Robinson tarafından geliştirilmiş bir tekniktir. Bu tekniğin esası şudur:

Eğer “veya” bağı ile bağlı P₁, ..., P_n önermelerinden bir Q önermesi dedüktif olarak çıkarılabiliyorsa, o zaman Q'nun değillemesini bu önermelere “ve” bağı ile kattığımız zaman bir çelişki elde ederiz. Sembollerle gösterecek olursak:

${\displaystyle P_{1}\land ,...,\land P_{n}\to Q}$

...çıkarımı geçerli ise,

${\displaystyle P_{1}\land ,...,\land P_{n}\land \neg Q}$

...bir çelişkidir.

Bu yöntemin kullanılabilmesi için, P₁, ..., P_n önermelerinin, eşdeğerlik dönüşümleri kullanılarak “birleşimli normal biçim” denilen bir biçime getirilmesi gerekir. Bu biçim sadece “değil”, “ve” ve “veya” mantıksal bağlaçlarını içerir.

Örnek 1:

 P -> Q ~P V Q ~P V Q P P P ------ ------ ~Q Q Q ------ 

Bu örnekte ${\displaystyle P\to Q}$ şartlı önermesi yerine, eşdeğeri ${\displaystyle \neg P\lor Q}$ konulmuştur ki bu, ${\displaystyle P\to Q}$ önermesinin normal biçimidir.

Örnek 2:

 A -> B ~A V B ~A V B B -> C ~B V C ~B V C A A A -------- --------- ~C C C --------- 

Çözülüm teorem ispatlama yöntemi, yüklemler mantığının teorem ispatlama problemlerinde de uygulanmaktadır. Yüklemler mantığında teorem ispatı sırasında bireysel sabitlerin değişkenlerin yerine konulmasına “birleştirme” denilir.

Örnek 3:

 P(x,y) -> Q(x) ~P(x,y) V Q(x) ~P(a,y) V Q(a) P(a,y) P(a,y) P(a,y) -------------- --------------- ~Q(a) Q(a) Q(a) --------------- 

Bulanık Mantık

Bulanık mantık 1960’ların ortalarında Lotfi Zadeh tarafından iki değerli mantık ve olasılık teorisine alternatif olarak geliştirilmiştir. Bulanık mantıkçılara göre iki değerli mantık ve kümeler teorisi daha genel çok değerli bir teorinin özel halidir. Zadeh (1965) bulanık kümeleri ve bulanık mantığı şu şekilde tanımlamaktadır: "Bulanık sistemlerde temel düşünce bulanık mantıkta doğruluk değerleri (veya bulanık kümelerde üyelik değerleri) 0 ile 1 arasında değişen değerlerdir ki burada 0 mutlak yanlış, 1 de mutlak doğru olmaktadır."

Doğal dilde kullandığımız birçok cümlede “az”, “çok”, “orta” gibi kalitatif niceleyiciler kullanıyoruz. Bu tür cümleleri bulanık mantığın gösterimi ile ifadelendirmek daha kolay olmaktadır. Bulanık mantıkta “Ahmet yaşlıdır” ve “Bugün hava sıcaktır” cümlelerindeki “yaşlı” ve “sıcak” ifadelerine iki değerli mantıktaki gibi “doğru” veya” yanlış” yerine 0 ile 1 arasında değer verilebilmektedir.

Bulanık mantığın formel tanımları

X, elemanları x’ler olan bir nesneler kümesi olsun, yani X = (x). X’in içinde bir A bulanık kümesi bir üyelik fonksiyonu mA(x) ile karakterize edilir. Bu fonksiyon X içindeki her nesneyi, 0 ile 1 arasındaki bir reel sayıya [0,1] tekabül ettirir. Yukarıdaki örnekte A, yaşlı insanlar kümesi olabilir. Ahmet de X insanlar genel kümesinin bir üyesi olarak yaşlı insanlardan biri olabilir, ki A’daki üyelik derecesine göre üyelik değeri [0,1] reel sayılar aralığında yer alır.

mA(x) değeri 1’e yaklaştığında x’in A içindeki “üyelik derecesi” artar. Bütün x’ler için mA(x) = 0 ise, A boş bir küme olur ve bütün x’ler için mA(x) = mB(x) olduğunda da A=B olur. Bulanık kümelerle ilgili tarifler de şöyledir:

m(karşıt A) = 1 – mA. 

Eğer X’in bütün x’leri için mC(x) = MAX[mA(x), mB(x)] ise, C, A ve B’nin birleşimidir.

Eğer X’in bütün x’leri için mC(x) = MIN[mA(x), mB(x)] ise, C, A ve B’nin arakesitidir.

>

Kaynakça

1. ^ Üniversite seviyesi yayınlardan bazıları Boolos, Burgess, and Jeffrey (2002), (2001), and Mendelson (1997). A classic graduate text by Shoenfield (2001) first appeared in 1967.