Doğrusal ve zamanla değişmeyen (DZD) sistemler, tüm sistemler ailesinin en önemli alt kümesini oluşturmaktadır. Bunun nedeni sahip oldukları iki özelliğin (1-Doğrusallık ve 2-Zamanla Değişmemek) sinyal işleme alanında kullanılan en temel matematiksel operatörlerin (Fourier dönüşümleri, , Sabit Katsayılı Doğrusal Diferensiyel Denklemler) doğası ile tam bir uyum sergilemesi ve böylece karmaşık problemlerin başarılı matematiksel çözümlerinin elde edilmesine olanak sağlamasıdır.
Bir sistemin DZD olabilmesi için şu iki özelliği taşıması gerekli ve yeterli koşuldur:
1- Doğrusallık:
Giriş-Çıkış ilişkisi , şeklinde ifade edilen sürekli zamanlı bir sisteme uygulanan iki giriş sinyali ve ve bu sinyallere karşılık alınan çıkış tepkileri de ve olsun. Bu sisteme uygulanacak üçüncü bir girişi de şeklinde (lineer kombinasyon) tanımlarsak, doğrusal bir sistemin çıkışının aşağıdakini sağlaması gerekir: (Süperpozisyon özelliği)
Burada a ve b sabit katsayıları karmaşık sayılar kümesine dahildir.
2- Zamanla Değişmeme:
Benzer şekilde, Giriş-Çıkış ilişkisi , şeklinde ifade edilen sürekli zamanlı bir sisteme uygulanan bir giriş ve karşılık gelen çıkış olsun. İkinci bir girişi şu şekilde tanımlarsak: , bu sistemin zamanla değişmeyen özelliği gösterebilmesi için ikinci sinyal için çıkışının aşağıdaki özelliği sağlaması gerekir:
Benzeri bir tanım ayrık zamanlı DZD sistemleri için de yapılabilir ve şu şekilde özetlenebilir:
Ayrık zamanlı bir sistemin DZD olabilmesi için aşağıdaki iki özelliği sağlaması gerekli ve yeterli koşuldur:
1-
2-
Aşağıdaki örnek(ler) verilen bir sistemin DZD olup olmadığını, matematiksel olarak, nasıl bulabileceğimizi gösterir:
Örnek 1
Giriş çıkış özelliği 
Doğrusallık Testi






Zamanla Değişmeme Testi




Dolayısı ile doğrusallık koşulunu sağlamayan bu sistem DZD değildir. Böylesi bir sistem için doğrusal olmayan-zamanla değişmeyen tanımı yapılabilir.
Örnek 2
Giriş çıkış özelliği 
Doğrusallık Testi






Zamanla Değişmeme Testi




Dolayısı ile doğrusallık koşuluğunu sağladığı halde zamanla değişmeme koşulunu sağlamayan bu sistem DZD değildir.
Kaynakça
- ^ "Arşivlenmiş kopya". 27 Ağustos 2016 tarihinde kaynağından . Erişim tarihi: 1 Temmuz 2016.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Dogrusal ve zamanla degismeyen DZD sistemler tum sistemler ailesinin en onemli alt kumesini olusturmaktadir Bunun nedeni sahip olduklari iki ozelligin 1 Dogrusallik ve 2 Zamanla Degismemek sinyal isleme alaninda kullanilan en temel matematiksel operatorlerin Fourier donusumleri Sabit Katsayili Dogrusal Diferensiyel Denklemler dogasi ile tam bir uyum sergilemesi ve boylece karmasik problemlerin basarili matematiksel cozumlerinin elde edilmesine olanak saglamasidir Bir sistemin DZD olabilmesi icin su iki ozelligi tasimasi gerekli ve yeterli kosuldur 1 Dogrusallik Giris Cikis iliskisi y t T x t displaystyle y t T x t seklinde ifade edilen surekli zamanli bir sisteme uygulanan iki giris sinyali x1 t displaystyle x 1 t ve x2 t displaystyle x 2 t ve bu sinyallere karsilik alinan cikis tepkileri de y1 t T x1 t displaystyle y 1 t T x 1 t ve y2 t T x2 t displaystyle y 2 t T x 2 t olsun Bu sisteme uygulanacak ucuncu bir girisi de x3 t ax1 t bx2 t displaystyle x 3 t ax 1 t bx 2 t seklinde lineer kombinasyon tanimlarsak dogrusal bir sistemin cikisinin asagidakini saglamasi gerekir Superpozisyon ozelligi y3 t T x3 t T ax1 t bx2 t aT x1 t bT x2 t ay1 t by2 t displaystyle y 3 t T x 3 t T ax 1 t bx 2 t aT x 1 t bT x 2 t ay 1 t by 2 t Burada a ve b sabit katsayilari karmasik sayilar kumesine dahildir 2 Zamanla Degismeme Benzer sekilde Giris Cikis iliskisi y t T x t displaystyle y t T x t seklinde ifade edilen surekli zamanli bir sisteme uygulanan bir giris x1 t displaystyle x 1 t ve karsilik gelen cikis y1 t T x1 t displaystyle y 1 t T x 1 t olsun Ikinci bir girisi su sekilde tanimlarsak x2 t x1 t d d R displaystyle x 2 t x 1 t d d in R bu sistemin zamanla degismeyen ozelligi gosterebilmesi icin ikinci sinyal icin cikisinin asagidaki ozelligi saglamasi gerekir y2 t T x2 t T x1 t d y1 t d displaystyle y 2 t triangleq T x 2 t T x 1 t d y 1 t d Benzeri bir tanim ayrik zamanli DZD sistemleri icin de yapilabilir ve su sekilde ozetlenebilir Ayrik zamanli bir sistemin DZD olabilmesi icin asagidaki iki ozelligi saglamasi gerekli ve yeterli kosuldur 1 y3 n T x3 n T ax1 n bx2 n aT x1 n bT x2 n ay1 n by2 n textstyle y 3 n T x 3 n T ax 1 n bx 2 n aT x 1 n bT x 2 n ay 1 n by 2 n 2 y2 n T x2 n T x1 n d y1 n d d Z textstyle y 2 n triangleq T x 2 n T x 1 n d y 1 n d d in Z Asagidaki ornek ler verilen bir sistemin DZD olup olmadigini matematiksel olarak nasil bulabilecegimizi gosterir Ornek 1Giris cikis ozelligi y t T x t e x t displaystyle y t T x t e x t olan surekli zamanli bir sistem DZD midir Dogrusallik Testi x1 t displaystyle x 1 t ve x2 t displaystyle x 2 t girisler icin cikislar y1 t e x1 t displaystyle y 1 t e x 1 t ve y2 t e x2 t displaystyle y 2 t e x 2 t olsun x3 t ax1 t bx2 t displaystyle x 3 t ax 1 t bx 2 t icin cikisy3 t T ax1 t bx2 t e ax1 t bx2 t e x1 t a e x1 t b y1 t a y2 t b ay1 t by2 t displaystyle y 3 t T ax 1 t bx 2 t e ax 1 t bx 2 t e x 1 t a cdot e x 1 t b y 1 t a cdot y 2 t b neq ay 1 t by 2 t oldugundan dogrusal degildir Zamanla Degismeme Testi x1 t displaystyle x 1 t girisi icin cikis y1 t e x1 t displaystyle y 1 t e x 1 t ikinci bir girisi x2 t x t d displaystyle x 2 t x t d seklinde tanimlarsak ilgili cikis y2 t T x1 t d e x1 t d y1 t d displaystyle y 2 t T x 1 t d e x 1 t d y 1 t d oldugu icin sistem zamanla degismeyen ozelligi gosterir Dolayisi ile dogrusallik kosulunu saglamayan bu sistem DZD degildir Boylesi bir sistem icin dogrusal olmayan zamanla degismeyen tanimi yapilabilir Ornek 2Giris cikis ozelligi y n T x n k 0M nx k displaystyle y n T x n sum k 0 M n x k olan ayrik zamanli bir sistem DZD midir Dogrusallik Testi x1 n displaystyle x 1 n ve x2 n displaystyle x 2 n girisler icin cikislar y1 n k 0M nx1 k displaystyle y 1 n sum k 0 M n x 1 k ve y2 n k 0M nx2 k displaystyle y 2 n sum k 0 M n x 2 k olsun x3 n ax1 n bx2 n displaystyle x 3 n ax 1 n bx 2 n icin cikisy3 n T ax1 n bx2 n k 0M n ax1 k bx2 k a k 0M nx1 k b k 0M nx2 k ay1 n by2 n displaystyle y 3 n T ax 1 n bx 2 n sum k 0 M n big ax 1 k bx 2 k big a sum k 0 M n x 1 k b sum k 0 M n x 2 k ay 1 n by 2 n oldugundan dogrusaldir Zamanla Degismeme Testi x1 n displaystyle x 1 n girisi icin cikis y1 n k 0M nx1 k displaystyle y 1 n sum k 0 M n x 1 k olsun ikinci bir girisi x2 n x n d displaystyle x 2 n x n d seklinde tanimlarsak ilgili cikis y2 n T x1 n d k 0M nx2 k k 0M nx1 k d k dM n dx1 k y1 n d k 0M n d x1 k displaystyle y 2 n T x 1 n d sum k 0 M n x 2 k sum k 0 M n x 1 k d sum k d M n d x 1 k neq y 1 n d sum k 0 M n d x 1 k oldugu icin sistem zamanla degismektedir Dolayisi ile dogrusallik kosulugunu sagladigi halde zamanla degismeme kosulunu saglamayan bu sistem DZD degildir Kaynakca Arsivlenmis kopya 27 Agustos 2016 tarihinde kaynagindan Erisim tarihi 1 Temmuz 2016
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans



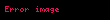


![{\textstyle y_{3}[n]=T\{x_{3}[n]\}=T\{ax_{1}[n]+bx_{2}[n]\}=aT\{x_{1}[n]\}+bT\{x_{2}[n]\}=ay_{1}[n]+by_{2}[n]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4Mk1UVXlZekUwTXpaaE1UQTVaRGsxWkRZeU5tTTFNelpoTURZMVpUVXpObU0xWW1RM05HRXouc3Zn.svg)
![{\textstyle y_{2}[n]\triangleq T\{x_{2}[n]\}=T\{x_{1}[n-d]\}=y_{1}[n-d]~~~,~~d\in Z}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5a1pqZGpaVFJoT1RjM1lXTTNNV1ZrWW1JeFlUVXlNRGhtTnpjellXRmxZbU5sWlRRd01qZ3cuc3Zn.svg)