Kısmi türev çok değişkenli bir işlevin(fonksiyon), sadece ilgili değişkeni sabit değilken alınan türevdir. Bu tarz türevleri içeren denklemlere kısmi diferansiyel denklem denir.
Tanım

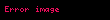
biçiminde tanımlanan n tane bağımsız değişkene bağlı sürekli z fonksiyonunun diğer değişkenler sabit tutularak herhangi bir değişkendeki 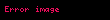
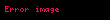

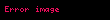
ifadesine 

şeklinde gösterilir.



Örnek:

wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kismi turev cok degiskenli bir islevin fonksiyon sadece ilgili degiskeni sabit degilken alinan turevdir Bu tarz turevleri iceren denklemlere kismi diferansiyel denklem denir Tanimz Rn Rn R displaystyle z mathbb R n times mathbb R n to mathbb R z f x1 x2 xm xn displaystyle z f x 1 x 2 x m x n biciminde tanimlanan n tane bagimsiz degiskene bagli surekli z fonksiyonunun diger degiskenler sabit tutularak herhangi bir degiskendeki Dxm displaystyle Delta x m degisimine karsilik fonksiyonun degisim hizi DzDxm f x1 x2 xm Dxm xn f x1 x2 xm xn Dxm displaystyle frac Delta z Delta x m frac f x 1 x 2 x m Delta x m x n f x 1 x 2 x m x n Delta x m Dxm h displaystyle Delta x m h z xm limh 0f x1 x2 xm h xn f x1 x2 xm xn h displaystyle frac partial z partial x m underset h to 0 mathop lim frac f x 1 x 2 x m h x n f x 1 x 2 x m x n h ifadesine z displaystyle z fonksiyonunun xm displaystyle x m degiskenine gore kismi turevi denir f xm fxm Dxmf z xm zxm displaystyle frac partial f partial x m f x m D x m f frac partial z partial x m z x m seklinde gosterilir z f x y displaystyle z f left x y right ise fx x y limh 0f x h y f x y h displaystyle f x left x y right underset h to 0 mathop lim frac f left x h y right f left x y right h fy x y limh 0f x y h f x y h displaystyle f y left x y right underset h to 0 mathop lim frac f left x y h right f left x y right h Ornek f x y x3 x2y y3fx x3 x x2y x y3 xfx 3x2 2xy 0fx 3x2 2xy displaystyle begin aligned amp f x y x 3 x 2 y y 3 amp f x left x 3 right x left x 2 y right x left y 3 right x amp f x 3 x 2 2xy 0 amp f x 3 x 2 2xy end aligned
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State