Bulanık küme (veya belirtisiz küme) kavramı, küme kavramının eleman olmanın derecelendirilmesine dayanan bir genelleştirilmesidir. Bulanık kümeler belirtisiz mantığın doğal bir genişlemesi olarak 1965 yılında Lütfi Aliaskerzade tarafından tanımlanmıştır. Bir nesne bir kümenin ya elemanı ya da elemanı değilken, bir bulanık kümenin belirli bir oranda kısmen elemanı olabilir.
Tanım



Bulanık küme farklı şekillerde de tanımlanabilir ancak kümenin her nokta için 
Bir 










Eğer bir 






Örneğin 




Bulanık alt küme



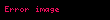






















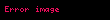


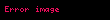




Bulanık kümeler üzerinde işlemler
Kümeler için tanımlı olan birleşim, kesişim, tümleme, kartezyen çarpım gibi işlemlerin tümü bulanık kümeler üzerine de taşınabilir.
İki bulanık kümenin birleşimi 




İki bulanık kümenin kesişimi ise 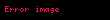











İki küme için tanımlanan bu işlemler ve yerine sırasıyla ve alınarak herhangi sayıdaki bulanık kümeler ailesine genişletilebilir.







Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bulanik kume veya belirtisiz kume kavrami kume kavraminin eleman olmanin derecelendirilmesine dayanan bir genellestirilmesidir Bulanik kumeler belirtisiz mantigin dogal bir genislemesi olarak 1965 yilinda Lutfi Aliaskerzade tarafindan tanimlanmistir Bir nesne bir kumenin ya elemani ya da elemani degilken bir bulanik kumenin belirli bir oranda kismen elemani olabilir TanimX displaystyle X bostan farkli bir evrensel kume olarak secilsin Bir A X 0 1 displaystyle A X to 0 1 fonksiyonuna X displaystyle X uzerinde bir bulanik kume adi verilir Bulanik kume farkli sekillerde de tanimlanabilir ancak kumenin her nokta icin 0 1 displaystyle 0 1 kapali araliginda bulunan bir uyelik degerine sahip olmasini anlatmasi bakimindan bu tanimlarin hepsi birbirine denktir Bir x displaystyle x X displaystyle X elemani icin A x displaystyle A x degerine x displaystyle x in A daki elemanlik derecesi denir Bu deger kimi zaman mA x displaystyle mu A x ile de gosterilir A x 1 displaystyle A x 1 olmasi klasik kume anlaminda x displaystyle x in A displaystyle A nin elemani olmasi A x 0 displaystyle A x 0 olmasi ise klasik kumelerdeki x displaystyle x in A displaystyle A nin elemani olmamasi durumuna denk gelir Eger bir x displaystyle x icin A x a displaystyle A x alpha ise x displaystyle x aA displaystyle A yazilir ve x displaystyle x in A displaystyle A bulanik kumesinin a displaystyle alpha derecesinde elemani oldugu soylenir Ornegin A x 0 5 displaystyle A x 0 5 yani x displaystyle x 0 5A displaystyle A olmasi x displaystyle x in A displaystyle A nin yari yariya elemani olmasi seklinde yorumlanir 1 klasik 0 klasik sembolune karsilik gelir Bulanik alt kumeA displaystyle A ve B displaystyle B bos olmayan bir X displaystyle X kumesi uzerinde iki bulanik kume olsun Her x X displaystyle x in X icin A x B x displaystyle A x leq B x oluyorsa A B displaystyle A subseteq B veya A B displaystyle A leq B yazilir ve A displaystyle A nin B displaystyle B nin bir bulanik alt kumesi oldugu soylenir A displaystyle A ve B displaystyle B bulanik kumelerinin esitligi her x displaystyle x X displaystyle X icin A x B x displaystyle A x B x olmasiyla tanimlanir Buna gore A displaystyle A nin B displaystyle B ye esit olmasi ayni zamanda hem A B displaystyle A subseteq B hem de B A displaystyle B subseteq A olmasi demektir X displaystyle X uzerindeki butun bulanik kumeler her x displaystyle x X displaystyle X icin X x 1 displaystyle X x 1 ile tanimlanan X displaystyle X bulanik kumesinin alt kumesiyken her x displaystyle x X displaystyle X icin x 0 displaystyle varnothing x 0 ile tanimlanan displaystyle varnothing bulanik kumesi X displaystyle X teki butun bulanik kumelerin alt kumesidir Bazen X displaystyle X ve displaystyle varnothing sembolleri yerine sirasiyla 1X displaystyle 1 X ve 0X displaystyle 0 X veya kisaca 1 displaystyle 1 ve 0 displaystyle 0 kullanilir Bulanik kumeler uzerinde islemlerKumeler icin tanimli olan birlesim kesisim tumleme kartezyen carpim gibi islemlerin tumu bulanik kumeler uzerine de tasinabilir Iki bulanik kumenin birlesimi A B displaystyle A cup B veya A B displaystyle A lor B ile gosterilir ve bu kumeye eleman olma derecesi her x displaystyle x X displaystyle X icin A B x maks A x B x displaystyle A cup B x maks A x B x olarak tanimlanir Iki bulanik kumenin kesisimi ise A B displaystyle A cap B veya A B displaystyle A land B ile gosterilir ve bu kumeye eleman olma derecesi her x displaystyle x X displaystyle X icin A B x min A x B x displaystyle A cap B x min A x B x olarak tanimlanir A displaystyle A ve B displaystyle B sirasiyla X displaystyle X ve Y displaystyle Y kumeleri uzerinde bulanik kumeler ise A B displaystyle A times B de X Y displaystyle X times Y uzerinde bir bulanik kumedir ve her x y X Y displaystyle x y in X times Y icin A B x y min A x B y displaystyle A times B x y min A x B y seklinde tanimlanir Iki kume icin tanimlanan bu islemler ve yerine sirasiyla ve alinarak herhangi sayidaki bulanik kumeler ailesine genisletilebilir A displaystyle A bulanik kumesinin tumleyeni Ac displaystyle A c veya A displaystyle A ile gosterilir ve her x displaystyle x A displaystyle A icin Ac x 1 A x displaystyle A c x 1 A x formuluyle belirlenir Klasik kumelerden farkli olarak bir A displaystyle A bulanik kumesi icin A Ac displaystyle A cap A c not varnothing olmasi mumkundur Ayrica bakinizKume Belirtisiz Mantik Bulanik Matematik
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans