Akım Fonksiyonu (veya Akış işlevi), eksen simetrisi ile üç boyutta olduğu kadar iki boyutta sıkıştırılamaz (ıraksama içermeyen) akışlar için tanımlanır. Akış hızı bileşenleri, skaler (sayıl alan) akış fonksiyonunun türevleri olarak ifade edilebilir. Akım fonksiyonu, kararlı akıştaki partiküllerin yörüngelerini gösteren akım çizgileri, çıkış çizgileri ve yörüngeyi çizmek için kullanılabilir. İki boyutlu Lagrange akım fonksiyonu, 1781'de Joseph Louis Lagrange tarafından tanıtıldı. Stokes akım fonksiyonu, eksenel simetrik üç boyutlu akış içindir ve adını George Gabriel Stokes'tan almıştır.

Herhangi iki noktadaki akım fonksiyonu değeri arasındaki fark, aynı iki noktayı birbirine bağlayan hat boyunca var olan hacimsel akış oranını () verir.
Akım çizgileri akıştaki hız vektörlerine teğet olduğu için, akım fonksiyonunun değeri akım çizgisi boyunca sabit olmak zorundadır. Akım fonksiyonunun kullanılabilirliği, verilmiş bir noktadaki x- ve y- yönlerindeki hız bileşenleri, bu noktadaki akım fonksiyonunun kısmi türevleri alınarak bulunur gerçeği altında yatar.
İki boyutlu için akım çizgileri çizgilere diktir. Hız potansiyeli ile birlikte alındığında, akım fonksiyonu karmaşık bir potansiyel türetmek için kullanılabilir. Akım fonksiyonu iki veya daha çok boyutlu bir akış için ifade edilebilir. Fakat iki boyutlu durum genellikle hesaplama ve görüntüleme bakımından en kolay olanıdır.
ile birlikte alındığı zaman akım fonksiyonu, potansiyel akışı türetmek için kullanılabilir. Diğer bir deyişle, akım fonksiyonu iki boyutlu Helmholtz dekompozisyonunun selonoidal kısmını ifade ederken, hız potansiyeli ise (Korunumlu vektör alanı) kısmını ifade eder.
İki Boyutlu Akım Fonksiyonu
Tanımlar

 ve
ve  noktaları arasındaki eğri boyunca hacim akısı
noktaları arasındaki eğri boyunca hacim akısıAkım fonksiyonunun simgesi kullanılan tanıma göre değişir.
Bunlardan birisi akım fonksiyonunu 
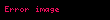
Kartezyen koordinat sistemi'nde aşağıdaki eşitlikteki gibidir




Alternatif Tanımı
Diğer bir tanımı ise şöyledir (genellikle meteoroloji ve okyanus biliminde kullanılır):
,

Burada kullanılan tanım, yukarıdakine göre ters işarete sahiptir (
İki Boyutlu Akım Fonksiyonunun Türevi
İki boyutlu düz bir akışta A ve B gibi iki farklı nokta farz edin. Eğer bu iki nokta arası uzaklık çok küçükse: δn ve bir akış bu iki noktalar arasında ortalama bir hızla hareket eder. q AB çizgisine diktir. Birim kalınlık başına düşen hacimsel akış oranı δΨ:
δn → 0, (δn sıfıra yaklaştıkça) yukarıdaki eşitlik düzenlenirse şunu elde etmiş oluruz:
Kartezyen Koordinatlardaki Akış
x-y kartezyen koordinat sistemindeki elementer bir alan içindeki akışı incelediğimizde şunu elde ederiz:
u hızı x eksenine paralel, v ise y eksenine paralel hızdır. Bu yüzden, δn → 0 yaklaştıkça:
Polar Koordinatlardaki Akış
r-θ polar koordinat sistemindeki çok küçük bir bölgeyi incelersek:
vr r eksenine paralel radyal hız bileşeni, vθ ise θ eksenine paralel teğetsel hız vektörüdür. Böylece, δn → 0 gittikçe ve eşitlik yeniden düzenlenince:
Süreklilik: Türev
Kartezyen koordinatlarda iki boyutlu düz bir akış düşünün. Süreklilik denklemi; elementer bir bölge içinde sıkıştırılamaz bir akış için, çıkan kütle giren kütleye eşittir.
Toplam akış aşağıdaki ifadeyle verilir:
Kontrol hacmi dışına çıkan toplam akış:
Böylelikle:
sadeleştirirsek:
Akım fonksiyonunun tanımı itibarıyla yukarıdaki eşitliği birleştirirsek:
bulmuş oluruz
Kaynakça
- ^ Lagrange, Joseph-Louis (1736-1813) Auteur du texte (1867-1892). Oeuvres de Lagrange. T. 4 / publiées par les soins de M. J.-A. Serret [et G. Darboux] ; [précédé d'une notice sur la vie et les ouvrages de J.-L. Lagrange, par M. Delambre] (Fransızca). IV. ss. 695-748. 27 Temmuz 2023 tarihinde kaynağından . Erişim tarihi: 27 Temmuz 2023.
- ^ Stokes, George Gabriel; Larmor, Joseph; Rayleigh, John William Strutt (1880-1905). Mathematical and physical papers. University of California Libraries. Cambridge : University Press.
- B. S. Massey and J. Ward-Smith, Mechanics of Fluids, 7th ed., Nelson Thornes, UK (1998).
- F. M. White, Fluid Mechanics, 5th ed., McGraw-Hill, New York (2003).
- T. W. Gamelin, Complex Analysis, Springer, New York (2001). .
- AMS Glossary of Meteorology entry:
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Akim Fonksiyonu veya Akis islevi eksen simetrisi ile uc boyutta oldugu kadar iki boyutta sikistirilamaz iraksama icermeyen akislar icin tanimlanir Akis hizi bilesenleri skaler sayil alan akis fonksiyonunun turevleri olarak ifade edilebilir Akim fonksiyonu kararli akistaki partikullerin yorungelerini gosteren akim cizgileri cikis cizgileri ve yorungeyi cizmek icin kullanilabilir Iki boyutlu Lagrange akim fonksiyonu 1781 de Joseph Louis Lagrange tarafindan tanitildi Stokes akim fonksiyonu eksenel simetrik uc boyutlu akis icindir ve adini George Gabriel Stokes tan almistir Akis cizgileri akim fonksiyonunun sabit degerine sahip cizgiler duzgun akista dairesel bir silindir etrafindaki sikistirilamaz potansiyel akis icin Herhangi iki noktadaki akim fonksiyonu degeri arasindaki fark ayni iki noktayi birbirine baglayan hat boyunca var olan hacimsel akis oranini verir Akim cizgileri akistaki hiz vektorlerine teget oldugu icin akim fonksiyonunun degeri akim cizgisi boyunca sabit olmak zorundadir Akim fonksiyonunun kullanilabilirligi verilmis bir noktadaki x ve y yonlerindeki hiz bilesenleri bu noktadaki akim fonksiyonunun kismi turevleri alinarak bulunur gercegi altinda yatar Iki boyutlu icin akim cizgileri cizgilere diktir Hiz potansiyeli ile birlikte alindiginda akim fonksiyonu karmasik bir potansiyel turetmek icin kullanilabilir Akim fonksiyonu iki veya daha cok boyutlu bir akis icin ifade edilebilir Fakat iki boyutlu durum genellikle hesaplama ve goruntuleme bakimindan en kolay olanidir ile birlikte alindigi zaman akim fonksiyonu potansiyel akisi turetmek icin kullanilabilir Diger bir deyisle akim fonksiyonu iki boyutlu Helmholtz dekompozisyonunun selonoidal kismini ifade ederken hiz potansiyeli ise Korunumlu vektor alani kismini ifade eder Iki Boyutlu Akim FonksiyonuTanimlar A displaystyle A ve P displaystyle P noktalari arasindaki egri boyunca hacim akisi Akim fonksiyonunun simgesi kullanilan tanima gore degisir Bunlardan birisi akim fonksiyonunu ps displaystyle psi iki boyutlu akis icin tanimlamaktir u ps displaystyle mathbf u nabla times boldsymbol psi ps 0 0 ps displaystyle boldsymbol psi 0 0 psi hiz vektoru u u v 0 displaystyle mathbf u u v 0 durumunda iken Kartezyen koordinat sistemi nde asagidaki esitlikteki gibidir u ps y v ps x displaystyle u frac partial psi partial y qquad v frac partial psi partial x u displaystyle u ve v displaystyle v hizlari sirasiyla kartezyen koordinatlardaki x displaystyle x ve y displaystyle y yonlerindeki hizlardir Alternatif Tanimi Diger bir tanimi ise soyledir genellikle meteoroloji ve okyanus biliminde kullanilir u z ps psy psx 0 displaystyle mathbf u mathbf z times nabla psi equiv psi y psi x 0 z displaystyle mathbf z z displaystyle z yonundeki birim vektordur ve and alt indisler kismi turevleri belirtir Burada kullanilan tanim yukaridakine gore ters isarete sahiptir ps ps displaystyle psi psi boylelikle kartezyen koordinatlardaki bicimi soyledir u ps y v ps x displaystyle u frac partial psi partial y qquad v frac partial psi partial x Iki Boyutlu Akim Fonksiyonunun Turevi Iki boyutlu duz bir akista A ve B gibi iki farkli nokta farz edin Eger bu iki nokta arasi uzaklik cok kucukse dn ve bir akis bu iki noktalar arasinda ortalama bir hizla hareket eder q AB cizgisine diktir Birim kalinlik basina dusen hacimsel akis orani dPS dps qdn displaystyle delta psi q delta n dn 0 dn sifira yaklastikca yukaridaki esitlik duzenlenirse sunu elde etmis oluruz q ps n displaystyle q frac partial psi partial n Kartezyen Koordinatlardaki Akis x y kartezyen koordinat sistemindeki elementer bir alan icindeki akisi inceledigimizde sunu elde ederiz dps udy displaystyle delta psi u delta y dps vdx displaystyle delta psi v delta x u hizi x eksenine paralel v ise y eksenine paralel hizdir Bu yuzden dn 0 yaklastikca u ps y displaystyle u frac partial psi partial y v ps x displaystyle v frac partial psi partial x Polar Koordinatlardaki Akis r 8 polar koordinat sistemindeki cok kucuk bir bolgeyi incelersek dps vr rd8 displaystyle delta psi v r r delta theta dps v8dr displaystyle delta psi v theta delta r vr r eksenine paralel radyal hiz bileseni v8 ise 8 eksenine paralel tegetsel hiz vektorudur Boylece dn 0 gittikce ve esitlik yeniden duzenlenince vr 1r ps 8 displaystyle v r frac 1 r frac partial psi partial theta v8 ps r displaystyle v theta frac partial psi partial r Sureklilik Turev Kartezyen koordinatlarda iki boyutlu duz bir akis dusunun Sureklilik denklemi elementer bir bolge icinde sikistirilamaz bir akis icin cikan kutle giren kutleye esittir Toplam akis asagidaki ifadeyle verilir dpsin udy vdx displaystyle delta psi in u delta y v delta x Kontrol hacmi disina cikan toplam akis dpsout u u xdx dy v v ydy dx displaystyle delta psi out left u frac partial u partial x delta x right delta y left v frac partial v partial y delta y right delta x Boylelikle dpsin dpsout displaystyle delta psi in delta psi out udy vdx u u xdx dy v v ydy dx displaystyle u delta y v delta x left u frac partial u partial x delta x right delta y left v frac partial v partial y delta y right delta x sadelestirirsek u x v y 0 displaystyle frac partial u partial x frac partial v partial y 0 Akim fonksiyonunun tanimi itibariyla yukaridaki esitligi birlestirirsek 2ps x y 2ps y x 0 displaystyle frac partial 2 psi partial x partial y frac partial 2 psi partial y partial x 0 bulmus oluruzKaynakca Lagrange Joseph Louis 1736 1813 Auteur du texte 1867 1892 Oeuvres de Lagrange T 4 publiees par les soins de M J A Serret et G Darboux precede d une notice sur la vie et les ouvrages de J L Lagrange par M Delambre Fransizca IV ss 695 748 27 Temmuz 2023 tarihinde kaynagindan Erisim tarihi 27 Temmuz 2023 Stokes George Gabriel Larmor Joseph Rayleigh John William Strutt 1880 1905 Mathematical and physical papers University of California Libraries Cambridge University Press B S Massey and J Ward Smith Mechanics of Fluids 7th ed Nelson Thornes UK 1998 F M White Fluid Mechanics 5th ed McGraw Hill New York 2003 T W Gamelin Complex Analysis Springer New York 2001 ISBN 0 387 95093 1 AMS Glossary of Meteorology entry
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans