Açısal momentum, herhangi bir cismin dönüş hareketine devam etme isteğinin bir göstergesidir ve bu nicelik cismin kütlesine, şekline ve hızına bağlıdır. Açısal momentum bir vektör birimidir ve cismin belirli eksenler üzerinde sahip olduğu dönüş eylemsizliği ile dönüş hızını ifade eder.
Bir sistemin sahip olduğu açısal momentum, içerisindeki bireysel ufak parçacıkların sahip olduğu açısal momentumların toplamına eşittir. Simetri ekseni üzerinde dönüş yapan bir cismin açısal momentumu eylemsizliğinin (cismin yerinin değiştirilmesine ile açısal hızına ω müdahale edilmesine karşı yaratmış olduğu direnç) ürünü olarak hesaplanabilir. Formülü 'dir. Bu nedenle açısal momentum bazen "dönüş lineer momentumu" olarak ifade edilir.[]

Kendi dönüş eksenine kıyasla çok daha ufak olan cisimlerde (örneğin çok uzun bir ip ucunda sallanan küçük lastik top veya Güneşin etrafında dönüş yapmakta olan gezegenler) açısal momentum, lineer dönüş momentumu olarak tanımlanabilir. Bu tanımda cismin kütlesi ve hızı dönüş ekseninin yarıçapı ile çarpılarak sonuç bulunur.
Sisteme dışarıdan herhangi bir tork uygulanmadığı sürece açısal momentum her zaman korunur. Örneğin buz pateni yapan biri kollarını içeriye doğru kapar ise kendisi hızlanır bunun sebebi açısal momentumun korunumudur. Nötron yıldızlarının çok fazla miktardaki dönüşleri de açısal momentumun korunuşu ile açıklanabilir. Açısal momentum korunumu çoğu fizik ve mühendislik bölümlerinde araç gereç üretiminde yararlanılmaktadır.
Klasik mekanikte açısal momentum
Bir merkeze göre alınan açısal momentum (L)un tanımı; 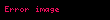
bu formülde r parçacığın merkeze göre yer vektörüdür, p parçacığın lineer momentumudur ve x vektör çarpımını ifade eder.

Tanımda da görüldüğü gibi açısal momentumun SI birimindeki değeri Newton metre saniyedir (N•m•s veya kg•m2/s) veya joule saniye (J•s). Vektör çarpımından dolayı açısal momentum, yarıçap vektörü r ve momentum vektörü p ye diktir ve bu sağ el kuralı ile bulunabilir. Sabit kütleli ve değişmeyen bir simetri ekseni etrafında dönüş yapan cismin açısal momentumu, eylemsizliğin ürünü olarak kabul edilir ve açısal hız vektörü; 
Bir parçacık topluluğunun açısal momentumu
Eğer bir sistem çok sayıda parçacık barındırıyorsa bu sistemin toplam açısal momentumu bu parçacıkların her birinin momentum toplamlarına eşittir. 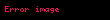
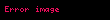

Kütle merkezi kullanılarak açısal momentum
Bir bütün halindeki parçacık gruplarının açısal momentumları bulunurken matematiksel işlemlerin kolaylığı açısından, kütle merkezi alınması genellikle uygun kabul edilir. Bir parçacık grubunun açısal momentumu her bir parçanın açısal momentumunun toplamına eşittir; 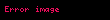
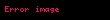

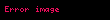
Ri i için kütle merkezine olan uzaklık, Vi i parçacığını lineer hızı ve sonuç olarak; 

görüldüğü gibi; 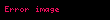
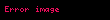
Bu sebeple bir noktaya göre alınan açısal momentum; 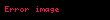
Yazılan ilk terim kütle merkezinin açısal momentumudur. Bu sonuç tek bir M kütleli cisim için kütle merkezinde v hızı ile hareket etmiş olsa idi aynı açısal momentum olurdu. Yazılan ikinci terim ise her bir parçacığın kendi içerisindeki açısal momentumlarıdır. İkinci terim daha da basitleştirilebilir. Kütle merkezindeki parçacıkların eylemsizlikleri ve açısal hızları dönüş hareketinden dolayı toplanır ve açısal momentumu verir.
Sabit eksende dönüş
Eğer bir sistemde sadece dönüş ile ilgileniyorsak, cismin açısal momentumunu skaler bir birimmiş gibi inceleyebiliriz ve bunun için saat yönünün tersinde hareket ettiği zamanları incelemeliyiz. Bunu yapabilmek için formülümüzde vektör çarpımının yerine birim vektörü ekleriz ve açısal momentum böylelikle son halini alır; 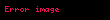

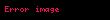
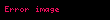
İşlem kolaylığı açısından düşünmemiz gereken kaldıraç kol uzaklığını merkeze ve p noktasından geçen bir çizgi üzerinde almamızdır. Bu tanımla beraber p noktasının yönünü (saat yönünü yoksa tersi mi) belirlenirse L nin işareti bulunabilir; 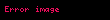
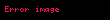
Sabit kütleli ve sabit bir eksen üzerinde dönüş yapan cisimlerin açısal momentumu eylemsizliğin bir ürünü olarak kabul edilebilir ve açısal hız vektörü; 


Açısal momentumun korunumu
Açısal momentumun korunumu yasası, kapalı bir sistemdeki cisme dışarıdan herhangi bir tork etki etmediği sürece açısal momentumda bir değişiklik olmayacağını tanımlar. Herhangi bir olay öncesinde cisim üzerinde sadece iç torklar etki ettiği için açısal momentumda bir dış tork olmadığı sürece değişme görülmez. Bu korunum yasası matematiksel olarak yön bağımsızlıktan bulunur ve sonsuz yön kabul edildiği için hiçbir yön bir diğerinden ayrı değildir. Noether teoreminde de görüldüğü gibi açısal momentumun zamana göre türevi torktur; 
Hız ve momentumun vektör çarpımı sıfırdır çünkü vektörler paraleldir. Sistemin kapalı olduğu kabul edilirse ve matematiksel olarak sıfır kabul edilirse dışarıdan etki edebilecek sıfır tork; 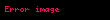
Eğer bir gezegenin beklenildiğinden daha yavaş hareket ettiği gözlemlenirse bunun sebebi gezegenin etrafında bir uydusu olmasıdır ve toplam açısal momentum gezegen ve uydusu arasında bölüşülür.
Açısal momentum genellikle kütleçekim kuvvetinin incelenmesinde kullanılmıştır. Eğer net kuvvet bir cismin sürekli olarak merkezine uygulanıyorsa bu cismin merkezine göre torku yoktur ve bu sebeple cismin açısal momentumu sabittir. Açısal momentumun sabit olması gezegenlerin yörüngelerini incelerken ve Bohr atom modelleri incelirken çok kullanışlıdır.

Açısal momentumun korunumunun en kolay açıklanabildiği olaylardan biri bir buz patencisinin hareketleridir. Kollarını dikey dönüş eksenine göre kapattığı zaman hızlanmaktadır. Kollarını kendine doğru çektiği zaman gövdesinin anlık eylemsizliğini düşürmektedir ve açısal momentum sabit olduğu için dışarıdan bir tork etki etmediği sürece açısal hız artacaktır.
Aynı olay çok hızlı dönmekte olan yıldızlar içinde geçerlidir (beyaz cüce, nötron yıldızları, kara delikler). Bu cisimler oluşurken kendilerinde daha büyük ve daha yavaş dönüş yapan yıldızlardan meydana gelmişlerdir (bir cismin boyutunun 104 azaltılması, açısal hızının 108 kat artmasına neden olur.
Dünya ve Ay arasındaki açısal momentumun korunumu aralarındaki açısal momentum transferleriyle gerçekleşir. Dünya ve Ay arasındaki bu geçişler dalga torklarında kaynaklanır. Bu olaylar dünyanın dönüş hızını yaklaşık 42 ns/gün [] azaltır ve Ay’ın yörüngesinin ~4.5 cm/yıl oranında [] artmasına neden olur.
Açısal momentum (modern tanım)
Modern (20.yüzyılda teoremsel fizik ve açısal momentum bir iç açısal momentum olarak kabul edilmemiştir) fizikte açısal momentum daha farklı bir yolla formülize edilmiştir.

Bu formülde açısal momentum, Noether birimlerini ikinci formu olarak kabul edilir. Sonuç olarak açısal momentum uzay zamanda genellikle korunmaz ta ki asimptotik olarak dönüşü değiştirilmez ise.
Klasik mekanikte bir parçacığın açısal momentumu bir düzlem elemanı olarak tanımlanabilir; 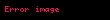
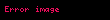

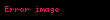
Göreceli mekanik ve göreceli açısal momentumda parçacıklar antisimetrik ikinci dereceden gergi ile ifade edilirler; 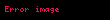
Kuantum mekaniğinde açısal momentum
Kuantum mekaniğindeki açısal momentum klasik fizikte anlatılmış olan açısal momentumdan biraz daha farklıdır. Göreceli kuantum mekaniğinde ise neredeyse bağlantıları kalmaz hale gelir çünkü açısal momentum artık tensörel çarpım haline gelmiştir.
Dönüş,orbital ve toplam açısal momentum

Sol: "Dönüş" açısal momentumu S cismin her bölgesindeki açısal momentumu belirtir.
Sağ: Açısal momentumunL herhangi bir eksendeki durumu,
Ūst: I ve açısal hız ω (L her zaman paralel değildir ω),
Alt: momentum p Yarıçapa göre r eksenden.
klasik açısal momentum tanımı; 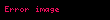
Ancak, kuantum fiziğinde bir başka açısal momentum türü vardır ve ismi dönüş açısal momentumudur ve S ile gösterilir. Neredeyse her element parçacığın dönüşü vardır. Dönüş genel olarak bir eksen üzerinde dönüş yapma olarak tanımlanır ancak bu eksik ve yanlış anlaşılma yaratan bir resimdir. Dönüş parçacıkların doğası olan bir olaydır ve orbital açısal momentumdan farklıdır. Her element parçacığın kendine ait dönüş özelliği vardır örneğin elektronların dönüşü her zaman 1/2 dir. Fotonların ise 1 dir.
Sonuç olarak toplam açısal momentum J, dönüş ve orbital açısal momentumun her parçacık için toplamını ifade eder. (bir parçacık için J= L + S). Açısal momentumun korunumu J için geçerlidir ancak L veya S e işlemez. Toplam korunduğu sürece açısal momentum S ve L arasında artıp azalabilir.
Nicemlenim
Kuantum mekaniğinde açısal momentum nicem bir yapıya sahiptir, yani sürekli olarak değişime uğrayamaz yalnız istenilen miktarlarda kuantum sıçramaları yapabilir. Herhangi bir sistem için aşağıda verilmiş uygulamalar her zaman geçerlidir. 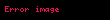
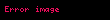
| Yapılan ... | Olabilecek sonuçlar... |
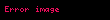 | 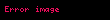 |
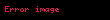 or or  | 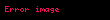 |
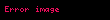 (  ) ) |  , burada , burada 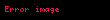 |
 or or 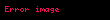 |  , burada , burada 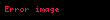 |

Düşürülmüş Planck sabiti 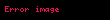
Kararsızlık

Dönüş üretebilen toplam açısal momentum
Yukarıda anlatıldığı gibi klasik mekanikteki açısal momentum L 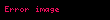
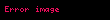

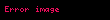
Açısal momentum işlemcisi ve dönüş işlemcisi arasındaki bağıntı lie matematiği ve lie grupları ile ifade edilebilir. Açısal momentum ve dönüş arasındaki bağıntı Noether teoreminde gösterilmiştir ve açısal momentumun fizik kuralları gereğince korunduğunu ispatlamıştır.
Elektrodinamikte açısal momentum
Yüklü bir parçacığın elektromagnetik alandaki hareketleri standart kabul edilen momentuma uymaktadır P. Standart açısal momentum L = r × P momentumu değişmez ölçülü değildir. Hatta fiziksel momentum olarak kabul edilen kinetik momentumUN SI birimi; 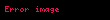
Kaynakça
- ^ Synge and Schild, Tensor calculus, Dover publications, 1978 edition, p. 161. .
- ^ R.P. Feynman, R.B. Leighton, M. Sands (1964). Feynman's Lectures on Physics (volume 2). Addison–Wesley. ss. 31-7. ISBN .
- ^ Littlejohn, Robert (2011). (PDF). bohr.physics.berkeley.edu. 26 Ağustos 2014 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 13 Ocak 2012.
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2006). Quantum Mechanics (2 volume set bas.). John Wiley & Sons. ISBN .
- Condon, E. U.; Shortley, G. H. (1935). "Especially Chapter 3". The Theory of Atomic Spectra. Cambridge University Press. ISBN .
- Edmonds, A. R. (1957). Angular Momentum in Quantum Mechanics. Princeton University Press. ISBN .
- Jackson, John David (1998). Classical Electrodynamics (3. bas.). John Wiley & Sons. ISBN .
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6. bas.). Brooks/Cole. ISBN .
- Thompson, William J. (1994). Angular Momentum: An Illustrated Guide to Rotational Symmetries for Physical Systems. Wiley. ISBN .
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5. bas.). W. H. Freeman. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Acisal momentum herhangi bir cismin donus hareketine devam etme isteginin bir gostergesidir ve bu nicelik cismin kutlesine sekline ve hizina baglidir Acisal momentum bir vektor birimidir ve cismin belirli eksenler uzerinde sahip oldugu donus eylemsizligi ile donus hizini ifade eder Bir sistemin sahip oldugu acisal momentum icerisindeki bireysel ufak parcaciklarin sahip oldugu acisal momentumlarin toplamina esittir Simetri ekseni uzerinde donus yapan bir cismin acisal momentumu eylemsizliginin cismin yerinin degistirilmesine ile acisal hizina w mudahale edilmesine karsi yaratmis oldugu direnc urunu olarak hesaplanabilir Formulu L Iw displaystyle mathbf L I boldsymbol omega dir Bu nedenle acisal momentum bazen donus lineer momentumu olarak ifade edilir kaynak belirtilmeli Jiroskop acisal momentumdan dolayi yukari yonde donmeye devam eder Kendi donus eksenine kiyasla cok daha ufak olan cisimlerde ornegin cok uzun bir ip ucunda sallanan kucuk lastik top veya Gunesin etrafinda donus yapmakta olan gezegenler acisal momentum lineer donus momentumu olarak tanimlanabilir Bu tanimda cismin kutlesi ve hizi donus ekseninin yaricapi ile carpilarak sonuc bulunur L r mv displaystyle mathbf L mathbf r times m mathbf v Sisteme disaridan herhangi bir tork uygulanmadigi surece acisal momentum her zaman korunur Ornegin buz pateni yapan biri kollarini iceriye dogru kapar ise kendisi hizlanir bunun sebebi acisal momentumun korunumudur Notron yildizlarinin cok fazla miktardaki donusleri de acisal momentumun korunusu ile aciklanabilir Acisal momentum korunumu cogu fizik ve muhendislik bolumlerinde arac gerec uretiminde yararlanilmaktadir Klasik mekanikte acisal momentumBir merkeze gore alinan acisal momentum L un tanimi L r p displaystyle mathbf L mathbf r times mathbf p bu formulde r parcacigin merkeze gore yer vektorudur p parcacigin lineer momentumudur ve x vektor carpimini ifade eder Donmekte olan bir sistemdeki kuvvet F tork t momentum p ve acisal momentum L vektorleri arasindaki iliski r yaricap Tanimda da goruldugu gibi acisal momentumun SI birimindeki degeri Newton metre saniyedir N m s veya kg m2 s veya joule saniye J s Vektor carpimindan dolayi acisal momentum yaricap vektoru r ve momentum vektoru p ye diktir ve bu sag el kurali ile bulunabilir Sabit kutleli ve degismeyen bir simetri ekseni etrafinda donus yapan cismin acisal momentumu eylemsizligin urunu olarak kabul edilir ve acisal hiz vektoru L Iw displaystyle mathbf L I boldsymbol omega I cismin eylemsizligi genellikle bir gergi birimi ve w acisal hizdir Duz bir cizgi ekseninde donus yapan parcacik veya kati cismin acisal momentumu bir vektordur ve buyuklugu ile yonu sabittir Eger donus ekseni cismin veya parcacigin merkezinden gecerse o noktada acisal momentum sifirdir Cunku bahsi gecen noktanin donus hareketi mevcut degildir Bir parcacik toplulugunun acisal momentumuEger bir sistem cok sayida parcacik barindiriyorsa bu sistemin toplam acisal momentumu bu parcaciklarin her birinin momentum toplamlarina esittir L nrn mnvn displaystyle mathbf L sum n mathbf r n times m n mathbf v n Sabit bir kutle dagiliminin oldugunu ve cismin kutlesinin r r r turevsel bir hiz elemani dV yon vektoru r bize kutle elementi dm r r dV verir Bu cismin bu sebeple sonsuz kucuk acisal momentumu dL r dmv r r r dVv dVr r r v displaystyle d mathbf L mathbf r times dm mathbf v mathbf r times rho mathbf r dV mathbf v dV mathbf r times rho mathbf r mathbf v dir Bu formul uzerinde yapilan turev ve integral islemleri sonucunda toplam acisal hiz bulunur L VdVr r r v displaystyle mathbf L int V dV mathbf r times rho mathbf r mathbf v Kutle merkezi kullanilarak acisal momentumBir butun halindeki parcacik gruplarinin acisal momentumlari bulunurken matematiksel islemlerin kolayligi acisindan kutle merkezi alinmasi genellikle uygun kabul edilir Bir parcacik grubunun acisal momentumu her bir parcanin acisal momentumunun toplamina esittir L i ri mivi displaystyle mathbf L sum i mathbf r i times m i mathbf v i ri i parcaciginin yer vektorudur mi kutlesi vi lineer hizidir Kutle merkezi su formul ile ifade edilmistir R 1M imiri displaystyle mathbf R frac 1 M sum i m i mathbf r i tum parcaciklarin toplam kutleleri M imi displaystyle M sum i m i Kutle merkezinin lineer hizi V 1M imivi displaystyle mathbf V frac 1 M sum i m i mathbf v i Ri i icin kutle merkezine olan uzaklik Vi i parcacigini lineer hizi ve sonuc olarak ri R Ri displaystyle mathbf r i mathbf R mathbf R i ve vi V Vi displaystyle mathbf v i mathbf V mathbf V i goruldugu gibi imiRi 0 displaystyle sum i m i mathbf R i 0 ve imiVi 0 displaystyle sum i m i mathbf V i 0 Bu sebeple bir noktaya gore alinan acisal momentum L iri mivi R MV i Ri miVi displaystyle mathbf L sum i mathbf r i times m i mathbf v i left mathbf R times M mathbf V right sum i mathbf R i times m i mathbf V i Yazilan ilk terim kutle merkezinin acisal momentumudur Bu sonuc tek bir M kutleli cisim icin kutle merkezinde v hizi ile hareket etmis olsa idi ayni acisal momentum olurdu Yazilan ikinci terim ise her bir parcacigin kendi icerisindeki acisal momentumlaridir Ikinci terim daha da basitlestirilebilir Kutle merkezindeki parcaciklarin eylemsizlikleri ve acisal hizlari donus hareketinden dolayi toplanir ve acisal momentumu verir Sabit eksende donusEger bir sistemde sadece donus ile ilgileniyorsak cismin acisal momentumunu skaler bir birimmis gibi inceleyebiliriz ve bunun icin saat yonunun tersinde hareket ettigi zamanlari incelemeliyiz Bunu yapabilmek icin formulumuzde vektor carpiminin yerine birim vektoru ekleriz ve acisal momentum boylelikle son halini alir L L r p sin 8r p displaystyle L mathbf L mathbf r mathbf p sin theta r p 8r p r ve p noktalari arasindaki hesaplanmis acidir Acisal momentumun skaler ve vektorel birimlerde gosterimi L p r displaystyle L pm mathbf p mathbf r perp r displaystyle mathbf r perp p ye gore kaldirac kol uzakligidir Islem kolayligi acisindan dusunmemiz gereken kaldirac kol uzakligini merkeze ve p noktasindan gecen bir cizgi uzerinde almamizdir Bu tanimla beraber p noktasinin yonunu saat yonunu yoksa tersi mi belirlenirse L nin isareti bulunabilir L r p displaystyle L pm mathbf r mathbf p perp p displaystyle mathbf p perp p nin r uzerindeki dik bilesenidir Goruldugu gibi acisal momentumun isareti donus yonune gore belirlenir Sabit kutleli ve sabit bir eksen uzerinde donus yapan cisimlerin acisal momentumu eylemsizligin bir urunu olarak kabul edilebilir ve acisal hiz vektoru L Iw displaystyle mathbf L I boldsymbol omega I cismin anlik eylemsizligidir ve w acisal hizdir Buyuk kutleli bir cismin kinetik enerjisi T T Iw22 displaystyle T frac I omega 2 2 formulu ile bulunabilir ve goruldugu gibi acisal hizi karesi kinetik enerji ile orantilidir Tipki otelenimsel enerji ve otelenimsel hiz gibi Genellikle acisal hiz vektoru donus ekseni yonunde iken acisal momentum bu yonde degildir Bunun sebebi cisim uzerindeki kutle dagiliminin nasil oldugunu bilmememizdendir Genellikle yonler ve buyuklukler arasindaki baglantilar w ve L yonleri eylemsizligin ikinci dereceden gergisinden bulunur Li Iijwj displaystyle L i I ij omega j gergi tanimlamasi uygulanir ve toplam islemleri yapilirsa i j 1 2 3 Kinetik enerjinin genel tanimi T 12wiIijwj displaystyle T dfrac 1 2 omega i I ij omega j Acisal momentumun korunumuAcisal momentumun korunumu yasasi kapali bir sistemdeki cisme disaridan herhangi bir tork etki etmedigi surece acisal momentumda bir degisiklik olmayacagini tanimlar Herhangi bir olay oncesinde cisim uzerinde sadece ic torklar etki ettigi icin acisal momentumda bir dis tork olmadigi surece degisme gorulmez Bu korunum yasasi matematiksel olarak yon bagimsizliktan bulunur ve sonsuz yon kabul edildigi icin hicbir yon bir digerinden ayri degildir Noether teoreminde de goruldugu gibi acisal momentumun zamana gore turevi torktur t dLdt drdt p r dpdt 0 r F r F displaystyle mathbf tau frac mathrm d mathbf L mathrm d t frac mathrm d mathbf r mathrm d t times mathbf p mathbf r times frac mathrm d mathbf p mathrm d t 0 mathbf r times mathbf F mathbf r times mathbf F Hiz ve momentumun vektor carpimi sifirdir cunku vektorler paraleldir Sistemin kapali oldugu kabul edilirse ve matematiksel olarak sifir kabul edilirse disaridan etki edebilecek sifir tork Lsystem constant text 0 displaystyle mathbf L mathrm system mathrm constant leftrightarrow sum mathbf tau mathrm ext 0 text displaystyle mathbf tau ext sistemdeki parcaciklara etki eden torktur Sistem icindeki kuvvetlerin Newton unun ucuncu yasasina uydugu kabul edilir Bu demektirki parcaciklarin birbirlerine uyguladigi kuvvetler birbirlerine esittir Yorungelerde ise acisal momentum gezegenin hem kendi etrafinda hem de yorungesi etrafindaki donusune dagilmistir Ltotal Lspin Lorbit displaystyle mathbf L mathrm total mathbf L mathrm spin mathbf L mathrm orbit Eger bir gezegenin beklenildiginden daha yavas hareket ettigi gozlemlenirse bunun sebebi gezegenin etrafinda bir uydusu olmasidir ve toplam acisal momentum gezegen ve uydusu arasinda bolusulur Acisal momentum genellikle kutlecekim kuvvetinin incelenmesinde kullanilmistir Eger net kuvvet bir cismin surekli olarak merkezine uygulaniyorsa bu cismin merkezine gore torku yoktur ve bu sebeple cismin acisal momentumu sabittir Acisal momentumun sabit olmasi gezegenlerin yorungelerini incelerken ve Bohr atom modelleri incelirken cok kullanislidir Iki zit yonlu kuvvet tarafindan olusturulan tork Fg and Fg acisal momentumda tork yonunde bir degisiklige sebep olur L Tork acisal momentumun turevidir Acisal momentumun korunumunun en kolay aciklanabildigi olaylardan biri bir buz patencisinin hareketleridir Kollarini dikey donus eksenine gore kapattigi zaman hizlanmaktadir Kollarini kendine dogru cektigi zaman govdesinin anlik eylemsizligini dusurmektedir ve acisal momentum sabit oldugu icin disaridan bir tork etki etmedigi surece acisal hiz artacaktir Ayni olay cok hizli donmekte olan yildizlar icinde gecerlidir beyaz cuce notron yildizlari kara delikler Bu cisimler olusurken kendilerinde daha buyuk ve daha yavas donus yapan yildizlardan meydana gelmislerdir bir cismin boyutunun 104 azaltilmasi acisal hizinin 108 kat artmasina neden olur Dunya ve Ay arasindaki acisal momentumun korunumu aralarindaki acisal momentum transferleriyle gerceklesir Dunya ve Ay arasindaki bu gecisler dalga torklarinda kaynaklanir Bu olaylar dunyanin donus hizini yaklasik 42 ns gun kaynak belirtilmeli azaltir ve Ay in yorungesinin 4 5 cm yil oraninda kaynak belirtilmeli artmasina neden olur Acisal momentum modern tanim Modern 20 yuzyilda teoremsel fizik ve acisal momentum bir ic acisal momentum olarak kabul edilmemistir fizikte acisal momentum daha farkli bir yolla formulize edilmistir Birlesik acisal momentumun birimlerinin 3 yer vektorleri x kutle m ve 3 momentum p Bu formulde acisal momentum Noether birimlerini ikinci formu olarak kabul edilir Sonuc olarak acisal momentum uzay zamanda genellikle korunmaz ta ki asimptotik olarak donusu degistirilmez ise Klasik mekanikte bir parcacigin acisal momentumu bir duzlem elemani olarak tanimlanabilir L r p displaystyle mathbf L mathbf r wedge mathbf p bu formulde dis carpim amp ve vektor carpimi x in yerini alir Bu daha basit bir geometrik duzlem olusturulmasini saglar ve x ile p vektorleri kullanilir Islemler iki veya daha fazla boyutlar icin gecerlidir Kartezyen koordinatlarda L xpy ypx ex ey ypz zpy ey ez zpx xpz ez ex Lxyex ey Lyzey ez Lzxez ex displaystyle begin array rl mathbf L amp left xp y yp x right mathbf e x wedge mathbf e y left yp z zp y right mathbf e y wedge mathbf e z left zp x xp z right mathbf e z wedge mathbf e x amp L xy mathbf e x wedge mathbf e y L yz mathbf e y wedge mathbf e z L zx mathbf e z wedge mathbf e x end array veya daha detayli ic gosterim ile Lij xipj xjpi displaystyle L ij x i p j x j p i Bu acisal hiz tanimi anti simetrik ikinci dereceden gergi olarak da tanimlanabilir birimleri wij Bu iki anti simetrik gerginin arasindaki baginti eylemsizlikle aciklanabilir ve gergi dorduncu dereceden olmalidir Lij Iijkℓwkℓ displaystyle L ij I ijk ell omega k ell Bu denklemdeki L ve w herhangi bir boyutta dogrulugunu korur Bu denklem geometrik matematiksel islemlerde de gorulur L ve w bu sefer ortak vektorlerdir ve eylemsizlik arasinda bir baglanti olusturur Goreceli mekanik ve goreceli acisal momentumda parcaciklar antisimetrik ikinci dereceden gergi ile ifade edilirler Mab Xa Pb XbPa displaystyle M alpha beta X alpha P beta X beta P alpha dilinde dort yer X ve dort momentum P yukarida ifade edilen L yi parcaciklarin kutle merkezi hareketiyle yok ederler Yukarida anlatilmis olan her durum icin coklu parcaciklarin oldugu bir sistemdeki acisal momentum oradaki her parcacigin ayri acisal momnetumunun toplamina esittir Kuantum mekaniginde acisal momentumKuantum mekanigindeki acisal momentum klasik fizikte anlatilmis olan acisal momentumdan biraz daha farklidir Goreceli kuantum mekaniginde ise neredeyse baglantilari kalmaz hale gelir cunku acisal momentum artik tensorel carpim haline gelmistir Donus orbital ve toplam acisal momentumKlasik bir cismin acisal momentumu Sol Donus acisal momentumu S cismin her bolgesindeki acisal momentumu belirtir Sag Acisal momentumunL herhangi bir eksendeki durumu ust I ve acisal hiz w L her zaman paralel degildir w Alt momentum p Yaricapa gore r eksenden klasik acisal momentum tanimi L r p displaystyle mathbf L mathbf r times mathbf p kuantum mekanigi ile daha ileriye tasinabilir r nin yerine kuantum yer islemcisi p nin yerine momentum islemcisi konulur L ise bir islemci haline donusur ve orbital acisal momentum islemcisi adini alir Ancak kuantum fiziginde bir baska acisal momentum turu vardir ve ismi donus acisal momentumudur ve S ile gosterilir Neredeyse her element parcacigin donusu vardir Donus genel olarak bir eksen uzerinde donus yapma olarak tanimlanir ancak bu eksik ve yanlis anlasilma yaratan bir resimdir Donus parcaciklarin dogasi olan bir olaydir ve orbital acisal momentumdan farklidir Her element parcacigin kendine ait donus ozelligi vardir ornegin elektronlarin donusu her zaman 1 2 dir Fotonlarin ise 1 dir Sonuc olarak toplam acisal momentum J donus ve orbital acisal momentumun her parcacik icin toplamini ifade eder bir parcacik icin J L S Acisal momentumun korunumu J icin gecerlidir ancak L veya S e islemez Toplam korundugu surece acisal momentum S ve L arasinda artip azalabilir NicemlenimKuantum mekaniginde acisal momentum nicem bir yapiya sahiptir yani surekli olarak degisime ugrayamaz yalniz istenilen miktarlarda kuantum sicramalari yapabilir Herhangi bir sistem icin asagida verilmis uygulamalar her zaman gecerlidir ℏ displaystyle hbar dusurulmus Planck sabiti n displaystyle hat n herhangi bir yon vektorudur x y z gibi Yapilan Olabilecek sonuclar Ln displaystyle L hat n 2ℏ ℏ 0 ℏ 2ℏ displaystyle ldots 2 hbar hbar 0 hbar 2 hbar ldots Sn displaystyle S hat n or Jn displaystyle J hat n 32ℏ ℏ 12ℏ 0 12ℏ ℏ 32ℏ displaystyle ldots frac 3 2 hbar hbar frac 1 2 hbar 0 frac 1 2 hbar hbar frac 3 2 hbar ldots L2 displaystyle L 2 Lx2 Ly2 Lz2 displaystyle L x 2 L y 2 L z 2 ℏ2n n 1 displaystyle hbar 2 n n 1 burada n 0 1 2 displaystyle n 0 1 2 ldots S2 displaystyle S 2 or J2 displaystyle J 2 ℏ2n n 1 displaystyle hbar 2 n n 1 burada n 0 12 1 32 displaystyle n 0 frac 1 2 1 frac 3 2 ldots Bir cember etrafindaki tam 8 dalga boyu olusturur Bu sabit dalgalar 0 1 2 degerleri alabilir ve tam olmayan sayi degerleri alamaz 8 3 gibi Dusurulmus Planck sabiti ℏ displaystyle hbar normal standartlarda 10 34J dir Bu sebepten oturu acisal momentumu nicem orani mikroskobik cisimleri etkileyemeyecek kadar kucuktur Ancak mikroskopik sistemlerde oldukca onemlidir Ornegin kimyada islenen elektron katman ve tabakalarinda acisal momentumun nicemlenimlenmesi cok onemlidir Acisal momentumun nicemlenimlenmesi ilk olarak Niels Bohr tarafindan Bohr atom modelinde ortaya sunulmustur KararsizlikL r p displaystyle mathbf L mathbf r times mathbf p formulunde alti adet islem elemani bulunmaktadir Bunlar yer islemcileri rx displaystyle r x ry displaystyle r y rz displaystyle r z ve momentum islemcileri px displaystyle p x py displaystyle p y pz displaystyle p z Heisenberg belirsizlik kuramlarina gore formulumuzde bulunan alti islem elemaninin kesin degerlerinin hepsi icin ayni anda bulunmasi mumkun degildir Bu sebeple bir parcacigin acisal momentumunu bulurken bazi kisitlamalarla karsilasiriz Yapilabilecek en tutarli hesaplamalar tek bir eksen ve duzlem uzerindeki acisal momentum vektorunun yon ve degerini bulmaktir Belirsizlik yasasinin ifade ettigi gibi acisal momentum islemcisinin degisik bilesenleri bir arada bulunamaz ornegin LxLy LyLx displaystyle L x L y neq L y L x Donus uretebilen toplam acisal momentumYukarida anlatildigi gibi klasik mekanikteki acisal momentum L L r p displaystyle mathbf L mathbf r times mathbf p ile ifade edilir ancak toplam acisal momentum J daha farkli ve basit bir yolla donus yaratan olarak ifade edilir ve islemcisi R n ϕ exp iℏϕJ n displaystyle R hat n phi equiv exp left frac i hbar phi mathbf J cdot hat mathbf n right donus islemcisidir ve her sistemde donusu ifade eder ϕ displaystyle phi acisi ile n displaystyle hat mathbf n ekseninde Acisal momentum islemcisi ve donus islemcisi arasindaki baginti lie matematigi ve lie gruplari ile ifade edilebilir Acisal momentum ve donus arasindaki baginti Noether teoreminde gosterilmistir ve acisal momentumun fizik kurallari geregince korundugunu ispatlamistir Elektrodinamikte acisal momentumYuklu bir parcacigin elektromagnetik alandaki hareketleri standart kabul edilen momentuma uymaktadir P Standart acisal momentum L r P momentumu degismez olculu degildir Hatta fiziksel momentum olarak kabul edilen kinetik momentumUN SI birimi p mv P eA displaystyle mathbf p m mathbf v mathbf P e mathbf A e parcacigin elektrik yuku A ise elektromagnetik alanin magnetik vektor potansiyelidir Degismez olculu acisal momentum kinetik acisal momentum olarak da bilinir su formulle bulunur K r P eA displaystyle mathbf K mathbf r times mathbf P e mathbf A Kuantum mekanigi ile ilgili baglantilar canonical commutation relations bulunmaktadir Kaynakca Synge and Schild Tensor calculus Dover publications 1978 edition p 161 ISBN 978 0486636122 R P Feynman R B Leighton M Sands 1964 Feynman s Lectures on Physics volume 2 Addison Wesley ss 31 7 ISBN 9 780 201 021172 KB1 bakim Birden fazla ad yazar listesi link Littlejohn Robert 2011 PDF bohr physics berkeley edu 26 Agustos 2014 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 13 Ocak 2012 Cohen Tannoudji Claude Diu Bernard Laloe Franck 2006 Quantum Mechanics 2 volume set bas John Wiley amp Sons ISBN 978 0 471 56952 7 Condon E U Shortley G H 1935 Especially Chapter 3 The Theory of Atomic Spectra Cambridge University Press ISBN 0 521 09209 4 Edmonds A R 1957 Angular Momentum in Quantum Mechanics Princeton University Press ISBN 0 691 07912 9 Jackson John David 1998 Classical Electrodynamics 3 bas John Wiley amp Sons ISBN 978 0 471 30932 1 Serway Raymond A Jewett John W 2004 Physics for Scientists and Engineers 6 bas Brooks Cole ISBN 0 534 40842 7 Thompson William J 1994 Angular Momentum An Illustrated Guide to Rotational Symmetries for Physical Systems Wiley ISBN 0 471 55264 X Tipler Paul 2004 Physics for Scientists and Engineers Mechanics Oscillations and Waves Thermodynamics 5 bas W H Freeman ISBN 0 7167 0809 4
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans