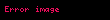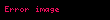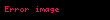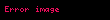Kalkülüste tek taraflı limit, x reel değişkenli bir f(x) fonksiyonun her iki limitidir. Burada x, ya üstten ya da alttan belirli bir noktaya yaklaşır. Bu limit şöyle sembolize edilebilir:
- veya veya ya da
a yaklaşım değerinde x azalan limittir (x, a ya "sağdan" veya "üstten" yaklaşır) ve şöyle ifade edilir.
- veya veya ya da
a yaklaşım değerinde x artan limittir (x, a ya "soldan" veya "alttan" yaklaşır)
x, a ya yaklaşırken eğer f(x) fonksiyonunun limiti, iki tek taraflı limite eşittir.
Bazı durumlarda yukarıdaki limit yoktur. Fakat yine de iki tek taraflı limit vardır. Bu nedenle x, a ya yaklaşırken fonksiyonun limiti bazen "iki taraflı limit" olarak adlandırılır. Bazı durumlarda iki tek taraflı limit vardır, bazı durumlarda yoktur.
Sağ taraflı limit tam olarak şöyle ifade edilebilir:
Benzer şekilde sol taraflı limit tam olarak şöyle ifade edilebilir:
Burada , tanım kümesi içindeki aralığı ifade eder.
Örnekler
Farklı tek taraflı limitlere sahip bir fonksiyona örnek aşağıda verilmiştir:
Oysa
Limitin topolojik tanımı ile ilişkisi
p noktasındaki tek taraflı limit, (limitin genel tanımına) karşılık gelir. Fonksiyonun tanım kümesi tek tarafta sınırlandırılır.
Abel teoremi
Bir önemli teorem, belirli kuvvet serisine sahip tek taraflı limitlerin kendi yakınsaklık mesafelerindeki davranışına Abel teoremi denir.
Ayrıca bakınız
Dış bağlantılar
- Tek taraflı limit, PlanetMath.org.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kalkuluste tek tarafli limit x reel degiskenli bir f x fonksiyonun her iki limitidir Burada x ya ustten ya da alttan belirli bir noktaya yaklasir Bu limit soyle sembolize edilebilir limx a f x displaystyle lim x to a f x veya limx af x displaystyle lim x downarrow a f x veya limx af x displaystyle lim x searrow a f x ya da limx gt a displaystyle lim x underset gt to a a yaklasim degerinde x azalan limittir x a ya sagdan veya ustten yaklasir ve soyle ifade edilir limx a f x displaystyle lim x to a f x veya limx af x displaystyle lim x uparrow a f x veya limx af x displaystyle lim x nearrow a f x ya da limx lt a displaystyle lim x underset lt to a a yaklasim degerinde x artan limittir x a ya soldan veya alttan yaklasir x a ya yaklasirken eger f x fonksiyonunun limiti iki tek tarafli limite esittir limx af x displaystyle lim x to a f x Bazi durumlarda yukaridaki limit yoktur Fakat yine de iki tek tarafli limit vardir Bu nedenle x a ya yaklasirken fonksiyonun limiti bazen iki tarafli limit olarak adlandirilir Bazi durumlarda iki tek tarafli limit vardir bazi durumlarda yoktur Sag tarafli limit tam olarak soyle ifade edilebilir e gt 0 d gt 0 x I 0 lt x a lt d f x L lt e displaystyle forall varepsilon gt 0 exists delta gt 0 forall x in I 0 lt x a lt delta Rightarrow f x L lt varepsilon Benzer sekilde sol tarafli limit tam olarak soyle ifade edilebilir e gt 0 d gt 0 x I 0 lt a x lt d f x L lt e displaystyle forall varepsilon gt 0 exists delta gt 0 forall x in I 0 lt a x lt delta Rightarrow f x L lt varepsilon Burada I displaystyle I f displaystyle f tanim kumesi icindeki araligi ifade eder OrneklerFarkli tek tarafli limitlere sahip bir fonksiyona ornek asagida verilmistir limx 0 11 2 1 x 1 displaystyle lim x rightarrow 0 1 over 1 2 1 x 1 Oysa limx 0 11 2 1 x 0 displaystyle lim x rightarrow 0 1 over 1 2 1 x 0 Limitin topolojik tanimi ile iliskisip noktasindaki tek tarafli limit limitin genel tanimina karsilik gelir Fonksiyonun tanim kumesi tek tarafta sinirlandirilir Abel teoremiBir onemli teorem belirli kuvvet serisine sahip tek tarafli limitlerin kendi yakinsaklik mesafelerindeki davranisina Abel teoremi denir Ayrica bakinizDis baglantilarTek tarafli limit PlanetMath org
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans