Matematikte, Artin Örgü Grubu olarak da bilinen n iplik üzerindeki örgü grubu ( ile gösterilir), elemanları n-örgülerin denklik sınıfları olan gruptur. Örgü gruplarının örnek uygulamaları arasında düğüm teorisi (knot theory), matematiksel fizikte; Artin'in örgü grubunun Yang-Baxter denklemine karşılık geldiği kanonik sunumu (matematiksel fizik konusu) ve cebirsel geometrinin monodromy değişmezleri yer alırlar.
Tarihi
Örgü grupları, 1925'te Emil Artin tarafından açık bir şekilde tanıtıldı, ancak (Wilhelm Magnus'un 1974'te işaret ettiği gibi), Adolf Hurwitz'in, 1891 yılı "Monodromy" çalışmasında zaten üstü kapalı bir şekilde geçiyordu. 1947'de Emil Artin tarafından açıkça tanımlanabileceği gibi, Örgü grupları ayrıca daha derin bir matematiksel yorumla da tanımlanır: belirli konfigürasyon uzaylarının temel grubu olarak.


⋅ 




⋅ 
⋅ 
Temel Özellikler




i) 
ii) 
Kısaca 



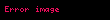


 ve
ve 

![image]()
ve
![image]()


![image]()
![image]()
ve
![image]()
Konfigürasyon Uzayı ile İlişkisi
Kompleks uzayda 
![image]()
Pür Örgü Grubu




Bir pür örgü 



Diğer Özellikler







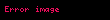











Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Artin Orgu Grubu olarak da bilinen n iplik uzerindeki orgu grubu Bn displaystyle B n ile gosterilir elemanlari n orgulerin denklik siniflari olan gruptur Orgu gruplarinin ornek uygulamalari arasinda dugum teorisi knot theory matematiksel fizikte Artin in orgu grubunun Yang Baxter denklemine karsilik geldigi kanonik sunumu matematiksel fizik konusu ve cebirsel geometrinin monodromy degismezleri yer alirlar TarihiOrgu gruplari 1925 te Emil Artin tarafindan acik bir sekilde tanitildi ancak Wilhelm Magnus un 1974 te isaret ettigi gibi Adolf Hurwitz in 1891 yili Monodromy calismasinda zaten ustu kapali bir sekilde geciyordu 1947 de Emil Artin tarafindan acikca tanimlanabilecegi gibi Orgu gruplari ayrica daha derin bir matematiksel yorumla da tanimlanir belirli konfigurasyon uzaylarinin temel grubu olarak I 0 1 displaystyle I 0 1 araligi olmak uzere asagidaki sartlari saglayan b R2 I displaystyle b subset mathbb R 2 times I kumesine n ipli orgu denir b displaystyle b kumesi n displaystyle n tane ayrik ipten olusur Bu iplerin her biri R2 I I displaystyle mathbb R 2 times I to I projeksiyonu altinda I displaystyle I birim araligina homeomorfdur Kisacasi her ip z t 0 t 1 displaystyle z t 0 leq t leq 1 duzleminden sadece bir kere gecmektedir b R2 0 1 0 2 0 n 0 0 displaystyle b cap mathbb R 2 times 0 1 0 2 0 n 0 times 0 b R2 1 1 0 2 0 n 0 1 displaystyle b cap mathbb R 2 times 1 1 0 2 0 n 0 times 1 Temel Ozelliklern displaystyle n tane ipten olusan ve Bn displaystyle B n olarak gosterilen bir Artin orgu grubu n 2 displaystyle n geq 2 icin s1 s2 sn 1 displaystyle sigma 1 sigma 2 ldots sigma n 1 uretecleri ile uretilen ve asagidaki iliskileri saglayan bir gruptur i sisj sjsi i j 2 displaystyle sigma i sigma j sigma j sigma i i j geq 2 ii si 1sisi 1 sisi 1si 1 i n 2 displaystyle sigma i 1 sigma i sigma i 1 sigma i sigma i 1 sigma i 1 leq i leq n 2 Kisaca Bn s1 s2 sn 1 displaystyle B n langle sigma 1 sigma 2 ldots sigma n 1 rangle seklinde de gosterilir B1 displaystyle mathbf B 1 orgu grubunda tum orguler tek bir ip uzerinde olusur Trivial bir gruptur B2 displaystyle mathbf B 2 grubundaki orguler iki ipin bukulmesi ile olusur Bir yonde bir bukum vererek 1 displaystyle 1 degeri ve diger yonde bir bukum ile 1 displaystyle 1 degeri elde edilir Bu sayede B2 displaystyle B 2 grubunun Z displaystyle mathbb Z grubuna izomorfik oldugu gorulur ve B3 s1 s2 s1s2s1 s2s1s2 displaystyle mathbf B 3 langle sigma 1 sigma 2 sigma 1 sigma 2 sigma 1 sigma 2 sigma 1 sigma 2 rangle grubu sonsuzdur ve degismeli degildir Elemanlari asagidaki gibidir ve B4 s1 s2 s3 s1s2s1 s2s1s2 s2s3s2 s3s2s3 ve s1s3 s3s1 displaystyle mathbf B 4 langle sigma 1 sigma 2 sigma 3 sigma 1 sigma 2 sigma 1 sigma 2 sigma 1 sigma 2 sigma 2 sigma 3 sigma 2 sigma 3 sigma 2 sigma 3 ve sigma 1 sigma 3 sigma 3 sigma 1 rangle grubundaki her orgu bu 3 orgu ve tersleri ile yazilabilir bu yuzden bu 3 orgu B4 displaystyle mathbf B 4 u temsil eder ve Konfigurasyon Uzayi ile Iliskisi Kompleks uzayda n displaystyle n tane sirali ve birbirinden farkli nokta dusunelim Bu noktalarin olusturdugu konfigurasyon uzayi asagidaki gibi tanimlanir Mn z1 zn Cn zi zj i j displaystyle operatorname M n z 1 ldots z n in mathbb C n z i neq z j forall i neq j Pur Orgu Grubu n displaystyle n ipten olusan pur orgu grubu PBn displaystyle operatorname PB n ile gosterilir ve Mn displaystyle operatorname M n uzayinin temel grubudur PBn p1 Mn displaystyle operatorname PB n pi 1 operatorname M n Bir pur orgu b p1 Mn displaystyle beta in pi 1 operatorname M n Mn displaystyle operatorname M n uzayi icerisinde bir dugumdur Yani ayni noktada baslayip ayni noktaya geri doner b 0 1 Mn displaystyle beta colon 0 1 to operatorname M n t b t b1 t bn t displaystyle t mapsto beta t beta 1 t ldots beta n t Diger Ozelliklern 1 displaystyle n 1 icin M1 C displaystyle operatorname M 1 mathbb C dir Rastgele bir z M1 displaystyle z in operatorname M 1 alalim O halde 1 displaystyle 1 ipli pur orgu grubu z displaystyle z den z displaystyle z ye giden morfizmalarin kumesi olur Sonuc olarak p1 M1 idz displaystyle pi 1 operatorname M 1 langle operatorname id z rangle elde edilir n 2 displaystyle n 2 olsun O halde M2 z1 z2 C2 z1 z2 displaystyle operatorname M 2 z 1 z 2 in mathbb C 2 z 1 neq z 2 olur Bu uzayin temel grubu Z displaystyle mathbb Z kumesine izomorftur Sonuc olarak PB2 Z displaystyle operatorname PB 2 cong mathbb Z SL2 Z displaystyle mathbf SL 2 mathbb Z Ozel lineer grup olarak adlandirilir determinanti 1 displaystyle 1 olan 2 2 displaystyle 2 times 2 tam sayi matrislerinin grubudur PSL2 Z displaystyle mathbf PSL 2 mathbb Z Projektif ozel lineer grup olarak adlandirilir SL2 Z displaystyle mathbf SL 2 mathbb Z I displaystyle pm I e esittir oyle ki I displaystyle I 2 2 displaystyle 2 times 2 birim matrislerdir Kaynakca Proceedings of the Second International Conference on the Theory of Groups Lecture Notes in Mathematics 372 Springer pp 463 487 ISBN 978 3 540 06845 7 Magnus Wilhem 10 Haziran 2018 tarihinde kaynagindan Emil Artin 1947 Theory of Braids 27 Ocak 2004 tarihinde kaynagindan arsivlendi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans







