Bu maddedeki bilgilerin için ek kaynaklar gerekli. (Aralık 2022) () |
Örnekleme istatistikte belirli bir yığından alınan kümeyi ifade eder. Örneğin; Türkiye'deki tüm üniversite sayıları bir yığın iken Ankara'daki üniversite sayısı bu yığından alınmış bir örnektir.
Örnek hesaplamalarında , , , , gibi semboller kullanılırken yığın hesaplamalarında ise bu simgelerin yerine sırası ile , , , , simgeleri kullanılır. İstatistik sadece örnekler üzerinde hesaplanabilir. Yığında ise parametre değerleri hesaplanır.
İstatistik bilim dalında örnekleme, N hacimli bir anakütleden, anakütleyi temsil edebilen n hacimli bir altküme elde edilmesidir. Tipik olarak anakütle çok büyüktür veya tüm anakütle elemanları hakkında bilgiler elde etmek imkânsızdır veya elde etmek için anakütleyi değiştirmek veya elemanlarına zarar vermek gerekecektir veya çok büyük masraf ve emek gerektirecektir. Bu nedenle ile tüm sayısal değerlerin öğrenilmesi istenmez. Örnekleme ile kullanılabilir bir büyüklükte altküme elde edilir. Örnek verileri toplanır; örnek verileri hakkında istatistikler hesaplanır ve örnek istatistikleri üzerinde çıkarımsal istatistik veya ekstrapolasyonlar kullanarak anakütle hakkında bilgiler elde edilir.
Örneğin, Türkiye'de üniversite öğrencilerinin fen bilimleri hakkındaki tavırları ölçülmek istensin ve bu tavırları açıklayan 10 soruluk bir anket hazırlanabileceği bilinsin. "Türkiye'de 2006-2007 öğretim yılında üniversite öğrencisi" olanların tümünün bu 10 soruya sayısal şekilde yanıt verdiği varsayılsın. Her bir soruya verilen yanıtın sayısal değerlerinin tümü birer anakütle olur. Burada dikkat edilecek nokta, istatistik bilimi için anakütlenin sayısal değerler olması ve üniversite öğrencisi olmamasıdır. Üniversite öğrencilerinin hepsi anakütle çerçevesi olarak anılır. Bu türlü sonuç bulmak ya imkânsızdır; ya da büyük emek, para ve zaman istemektedir. Bu nedenle örnekleme metodunun uygulanması tercih edilir.
Bu anakütlenin örneklemini elde etmek için anakütle çerçevesi olan 2006-2007 öğretim yılında Türkiye'deki üniversitelerde okuyanlardan küçük bir grup seçilir. Bu, daha küçük grup elemanlarına örnekleme çerçevesi adı verilir. Eğer her üniversiteden uygun bir sayıda öğrenci çeşitli kullanarak seçilirse, bunların tümü örnekleme çerçevesini oluşturur. Yine örneği açıklamaya devam edersek, bu daha nispeten küçük gruba (dikkat edilirse örneğinde verilen örnekleme çerçevesi yine de sayıca küçük olmaz) bu hazırlanmış on soruluk anket uygulanır. Her 10 soruya bu küçük grup elemanlarının verdiği sayısal yanıtlar birer örnekleme olur. Örnek, örnekleme çerçevesi üzerinde belirlenmiş bir değişken üzerinde yapılan sayım veya ölçüm ile elde edilen sayısal verilerdir. Tekrar dikkat çekilmelidir ki istatistik bilimi için örnek kavramı özel bir şekildedir ve genelde kullanılan örnek sözcüğü anlamından değişiktir. İstatistik için örnekleme çerçevesi elamanları (bu örnekte seçilen üniversite öğrencileri) örneği oluşturmazlar; her örnek çerçevesi elemanından bir değişken hakkında elde edilen sayısal veriler (bu örnekte her bir 10 soruya verilen sayısal yanıtlar) örnek oluştururlar.
Örnekleme teknikleri
Genel örnekleme tekniği tanımı
Yukarıda anakütle çerçevesinden uygun bir şekilde bir daha ufak örnekleme çerçevesi elde edilir denilmişti; işte bu uygun şekillerin incelenmesi örnekleme tekniklerinin incelenmesi demektir. Genel olarak örnekleme çerçevesinin anakütle çerçevesinden elde edilmesi için prensip örnekleme çerçevesinin anakütleyi temsil edici olmasıdır. Örnek verileri bir art fikirle bazı kişisel veya grupsal fikir ve prensiplere güya bilimsel bir destek sağlamak için kullanılmaması gerekmektedir; ama ne yazıktır ki pratikte birçok ticari, sınai, sosyal ve politik örnek bu niyetle elde edilip kullanılmakta ve genel gerçekte temsilci olma prensibinden uzaklaşılmaktadır. Bu istatistikle yalan söyleme şeklinde adlandırılabilen birçok araştırmalarda ele alınan bir konu olmuştur.
Eğer temsilci olma prensibine uygunluk arzu edilmekte ise örnekleme tekniği seçimi için iki genel teknik grubu bulunmaktadır:
- İstatistiksel olasılık prensiplerine dayanmayan teknikler ve
- İstatistik olasılık prensiplerine dayanan rastgele örnekleme teknikleri.
Bu kavramsal ayrımı sağlayan prensip, olasılık prensipleridir ve bu prensiplere uyan örnekler rastgele örnek adı ile anılmaktadır. Rastgele örnek için kullanılan prensip genel olarak
- anakütle çerçevesi içinde bulunan her elemanın örnek çerçevesi içine alınma olasılığının önceden belirlenmiş bir olasılık dağılımına göre olmasıdır.
Fakat genel olarak seçilen olasılık dağılımı Bernoulli dağılımı olduğu için birçok referansta bu prensip
- anakütle çerçevesi içinde bulunan her elemanın örnek çerçevesi içine alınma olasılığının eşit ve aynı olmasıdır.
şeklinde ifade edilmektedir. Dikkat edilirse rastgele örnek için temsilcilik prensibi özel olarak matematik-istatistik içeriğine göre değiştirilmiştir; belirlenmiş bir dağılıma göre olasılık, eşit olasılık prensibi ön plana alınmıştır. Eğer anakütle elemanları için bu prensip uygulanırsa, bunun mantıksal olarak temsilcilik prensibine uyacağı da ima edilmektedir. Burada bu iki grup örnekleme tekniğine ait olan teknikler genel olarak detaya inmeden açıklanacaktır.
Olasılık prensiplerine uymayan örnekleme teknikleri
Elverişlilik örneği
Elverişlilik örneği metodunda örnek çerçevesine girecek anakütle elemanları araştırmayı yapanın keyfine göre plansız tasarımsız seçilir. Örnek seçiminde önemi olan prensip elde edilen örneğin istatistik araştırmayı yapan kişi için elverişli olmasıdır. Eğer araştırmacı bilinçli, inanılır ve güvenilir bir kişi ise örnekin anakütlenin temsilcisi olma imkânı vardır ama bunun gerçekte geçerli olup olmadığını kontrol edecek hiçbir alet veya kural ortada bulunmamaktadır. Bu çeşit örnekleme daha sonra bir rastgele örnek almak için bir pilot çalışma için kullanılması çok kere tavsiye edilmektedir.
Mekanik örnekleme
Laboratuvarlarda, fabrikalarda ve diğer üretim kurumlarında test ve kontrol maksadı ile katı maddeler, sıvılar veya gazlar mekanik araç ve gereçler kullanılarak örneklem alınır. Özellikle kalite kontrolü sürecinde ve diğer testler ve kontrollar için bu mekanik örneklerin anakütlelerinin temsilcisi olması gerekmektedir.
Yargısal örnekleme
Yargısal örnekleme bir uzman kişi veya bilirkişinin kendi özel bilgisini ve yargısını kullanarak temsilci olma niceliğini taşıyan elemanlar ile bir örnekleme çerçevesi kurmasıdır.
Bu çeşit örneklerde çok kere bilinmeyen ve daha önceden hiç tahmin edilme imkânı olmayan yanlılıklar ortaya çıkar. Örnek seçme usulu ve protokollerinin kuruluşu ve kullanışı sırasında şeffaflık olmadığı için bilinmezliklerin nerede ve nasıl ortaya çıkabilecekleri ve nasıl yanlılıkların aksi tesirlerinin, nasıl çarelerle giderilebileceği bilinmez.
Bazı hallerde yargısal örnekleme kullanışlı ve hatta tercih edilir örnek alma tekniği olabilir. Rastgele örneklemenin imkânsız veya çok büyük zaman, emek ve para sarfı gerektirdiği için kullanışsız olduğu hallerde yargısal örnekleme gayeye uygun veriler ortaya çıkartabilir. Diğer bir uygun olma hali eğer kullanılacak örnek çok küçük ise ('10' veya daha aşağı sayıda veri öngörülüyorsa), bir rastgele örneke nazaran, bir yargısal örnek bulmak daha güvenilir ve daha iyi temsilci olma özelliği taşıyan bir örneklem ortaya çıkartabilir. Bazen kasten hiç temsilci olmayan ve gayet yanlı bir örnek kasten seçilmek istenebilir ve bu halde yargısal örnek tercih edilir. Bu kasten yanlı olarak yargısal örnek seçimi, araştırma konusunun en fena alternatif halini incelemek için çok uygundur.
Kota örneği
Bu çeşit örneklemede anakütlede tabakalar bulunduğu ve bu tabakalara ait olan elemanların birbirlerine çok benzer özellikler gösterdiği, fakat değişik tabakaya mensup elemanların özelliklerinden açıkça farklı oldukları bilinmektedir. Araştırmacı önce bu tabakaların özelliklerini tam olarak saptar ve değişik tabakaları birbirinden ayırt eden özellikleri tespit eder. Çok kere bu tabakaları ayırt edici özellikler kişilerin sosyo-demografik özellikleri olur. Buraya kadar yapılan işlemler aynen olasılık prensibine uyan tabakalı örneklemede de uygulanır.
İkinci adım olarak kota örneklemede her veri toplayıcısına, tespit edilmiş her tabaka için aldıkları örnekte (çok kere anket sorularını cevaplandırıcı sayısı olan) kaç gözlem ile bulunacağını tespit eden bir kota sayısı verilir.
Bundan sonra veri toplayıcılar kendilerine verilen her tabaka için kota sayısına göre kendi şahsi yargılarını kullanarak veri toplarlar. Bu adım tıpkı bir yargısal örnekleme gibidir; ama yargıyı uygulayanlar çok defa, uzman kişi veya bilirkişiler değil, gerçek veri toplayıcılardır.
Kartopu örneklemesi
Bu örneklemede önce bir çekirdek örneklem, elverişlilik örneği gibi araştırmayı yapan tarafından kendi keyfine göre bulunur. Ondan sonraki örneklem elemanları ise daha önce bulunmuş olan (çekirdek elemanlar ve onların seçtiği diğer) elemanlar tarafından bulunurlar. Örnek böylece, sanki karda itilerek büyüyen, bir kartopu gibi büyüme gösterir.
Rastgele örnekleme
Rastgele örnekleme olasılık örneklemesi olarak da adlandırılır.Rastgele örnek bulma ve kullanma için istenilen özellik:
- "Her bir anakütle elemanının belirli olasılıkla örnekte bulunmasıdır."
Bundan açıktır ki istenilen özellik doğrudan doğruya örneğin anakütle için temsilci olması değildir. Temsilci olma prensibine rastgele örnekleme biraz dolaylı olarak varmaktadır. Rastgele örnekleme kavramı ve prensibi temsilci olmama riskini bir seri istatistik teori kavramı ile niceliksel olarak açığa çıkarmaya yöneliktir. Bu niceliksel sonuçlar önce hangi çeşit rastgele örneklemenin seçilmesi ve sonra ne kadar büyük bir örnek hacmi elde edilmesi gerektiğine karar vermekte kullanılır. Bu örnek alınmasından önce karar verme yanında, örnek alındıktan sonra ölçülmüş sonuçlara bağlı örnekleme hatasını hesaplamaya yardım sağlar.
Belirli olasılık teriminin tanımlanmasına göre değişik türlü rastgele örnek ortaya çıkabilir. Bunlardan en iyi bilineni basit rastgele örneklemedir. Bu türlü örneklemenin ana prensibi her bir anakütle elemanının aynı olasılıkla örnekleme girebilmesidir. Yani her bir anakütle elemanı için örnekte bulunma olasılığı bir Bernoulli dağılımı gösterir. Diğer türlü belirli olasılık her bir anakütle elemanının Poisson dağılımına göre (birbirine eşit olmayarak) örnek içinde bulunmasıdır.
Ancak rastgele örneklemeler için sınıflandırma (gösterilen olasılık dağılımına göre yapılmamakta) daha pratik olarak nasıl rastgele olmanın sağlanma yöntemine dayanılmaktadır. Bu sınıflandırmaya göre rastgele örnekleme sınıfı içinde şu değişik örnekleme tipi mevcuttur:
- Basit rastgele örnekleme
- Örüntülü örnekleme
- Tabakalı örnekleme
- Küme örneklemesi
- Çok aşamalı örnekleme
- Eşli rastgele örnekleme
Basit rastgele örnekleme
Basit rastgele örneklem almanın ana prensibi her bir anakütle elemanının aynı olasılıkla örneğe girebilmesidir. Bu bir olasılık örneği tanımına uyar, çünkü her bir anakütle elemanı için örneklemde bulunma olasılığı bir Bernoulli dağılımı gösterir. Eğer anakütle büyüklüğü N ile ifade edilirse, her bir anakütle elemanı 1/N olasılıkla örnekte bulunur.
Bu prensibi uygulamak için şu aşamalar uygulanır:
- Anakütlenin her bir elemanı tespit edilir ve tespit edilen elamanların her birine bir sayısal kod verilir. Genellikle kodlar birbirini takip eden sayılar halinde sıralama düzeni halindedir ve sanki sayısal bir isimdir.
- İkinci aşamada en uygun örneklem hacmi, yani n, tayin edilir.
- Bir rastgele numara üretici alet kullanılarak istenilen n sayıda (birbirinden değişik olması tercih edilir) rastgele sayı çıkartılır. Rassal sayılar gayet çok olduğu için bir çeşit geri koymadan örnek alma deneyim sonucu olan n tane rastgele sayı aynı olasılığa haizdir.
- Bu rastgele n numara anakütle elemanlarının kodları ile karşılaştırılır. Kod numarası, çekilmiş olan rastgele sayıya eşit olan elemanlar örnek elemanı olarak seçilirler.
Örüntülü örnekleme
Bu olasılık örnekleme yöntemin ana prensibi bir içinde bulunan her bir elemana sıra bir kod numarası verilebilirse, rastgele seçilmiş veya hesaplama ile bulunmuş bir kod aralığı olan k aralığı ile her kinci elemanın gözlem yapılacak örnekleme seçimidir. Örneğin, belli bir üniversitede kayıtlı öğrenci numaraları belli bir numaradan başlayıp giden bir sıraya tabi iseler ilk olarak bir rastgele kayıt numarası seçilir ve sonra bir rastgele aralık numarası seçilir; diyelim 54 başlangıç kayıt numarası ve 12 de kod aralığı rastgele seçilmiş olsun. Örüntülü örneklemede örneğe dahil edilecek öğrenci elamanlarin şu kayıt numaraları olmalıdır:
- 54 66 78 90 ...... önceden seçilmiş n tane örneklem hacmi elde edilinceye kadar..
Tabakalı örnekleme
Bu çeşit olasılık örnekleme yönteminde anakütlenin tabakalardan oluştuğu gerçeği kabul edilmektedir. Her tabaka elemanı bir veya bir grup teşhis edici değişken değeri dolayısıyla birbirlerine çok benzedikleri kabul edilirler. Bu çeşit teşhis edici değişken(ler) için değerler tabakalar arasında çok farklıdır. Birçok sosyal bilim araştırması için bu teşhis edici değişken bir veya birkaç şahsi veya ekonomik veya sosyal özelliklerden oluşur.
Örneğin temsilcilik prensibine uyması için anakütlenin her bir tabakasından değişik sayıda örnek seçilir ve örnek de (ayni anakütle gibi) tabakalı olur. Genel olarak her anakütle tabakası ve örnek tabakası elemanları arasında ilişki kurulabilir. Orantılı tabakalar denilebilen bir tipe göre anakütle içinde her bir tabakanın toplama oranı, örnek tabakasının örnek büyüklük hacmine oranı ile aynıdır. Bu oran en popüler olarak tabaka içindeki teşhis edici değişiklik karakteri taşıyan elemanların sayısı ile toplam orantılıdır. Diğer bir alternatif standart sapmaların oranı olabilir. Diğer alternatifte orantısız tabakalar adı verilir ve daha başka yargısal seçimlerle örnek tabaka elemanları anakütle tabakalarına temsilci olması sağlanır.
Küme örneklemesi
Bu şekilde örnekleme genellikle örnekleme zaman ve para maliyetlerini düşük tutmak için kullanılmaktadır. Anakütle çerçevesi elamanlarının birbirine yakın kümeler oluşturduğu hallerde ve her bir küme genel olarak diğer kümelere çok benzerlerse, bu tipi örnekleme kullanılması uygun olabilir. Örneğin, anakütle çerçevesi belli bir üniversite olursa, o üniversite içindeki değişik bölümlerde bulunan öğrencilerin benzer özellikler gösterdikleri kabul edilebilir ve bölümler incelenen sorun için birbirinden çok değişik değillerse, bölümler birer küme olarak incelemeye taban olabilirler. Bu kümeler mekan içinde (örneğin şehrin değişik mahalleleri veya Amerika'daki gibi değişik şehir blokları) veya zaman içinde (belirli zaman dönemleri) olabilir.
Küme örneklemesi iki aşamada yapılır:
- Birinci aşamada çok iyi belirlenmiş kümeler tespit edilir. Her iyi belirlenmiş kümeye bir kod numarası verilir. Bütün kod numaraları içinden basit rastgele örnekleme ile küçük sayıda 'kümeler örneği' seçilir. Örneğin, bir üniversite 35 tane bölümden oluşmuşsa ve her bölüme ait öğrenci üyeler iyice tespit edilmişlerse; her bir bölüm kodlanır ve diyelim 8 tane bölüm bu 35 bölümden basit rastgele örnek olarak (yani 35 bölüm de örneğe dahil olmak için aynı olasılığı taşıyarak) seçilirler.
- İkinci aşamada her bir örneğe giren küme içinde bulunan bütün anakütle elemanları üzerinde gözlem yapılır. Yani her örnek küme için tam sayım yapılır. Örneğin, ilk aşamada seçilmiş olan 8 bölümdeki her öğrenci elemanlarının tümüne gözlem uygulanır.
Doğal olarak, tüm anakütle çerçevesi seçilmediği için zaman ve para maliyetleri tam sayımdan düşük olur. Dikkat edilirse bu çeşit örneklemede rastgele seçilme kümelerle ilgilidir. Bu seçim yapıldıktan sonra seçilen kümeler içinde bulunan birbirine yakın elemanlar gözümlendiği için de maliyetler (özellikle basit rastgele örneklemeye kıyasla) daha düşük olması çok mümkündür. Basit rastgele örneklemeye kıyasla küme örneklemesinin bir diğer avantajı, tüm anakütle elemanlarının her birinin kodlanmasının gerekmediğidir; bu tüm kodlama büyük maliyet gerektirir ve bazen de imkânsızdır. Buna karşılık küme örneklemesinde sadece birinci aşamada seçilmiş olan kümeler elemanları tespit edilip kodlanır.
Ancak küme örneklemesi, her bir kümenin diğer kümelere benzediğine ve sadece kendine has karakteri olan bir veya birkaç kümenin bulunmadığı varsayımına dayanır. Gerçekte bu varsayım her zaman ancak yaklaşık olarak doğru olacak ve bazı belirlenen kümeler kendine has karakter arz edecektir. Bu nedenle küme örneklemesinin yayılımı ayni anakütle için alınabilecek basit rastgele örneklemeden daha fazla olacaktır ve örneklemeden sonra elde edilecek kestirimler veya yapılan sınamalar daha az tutarlı olacak ve daha fazla yanlı olma olasılığı taşıyacaklardır.
Çok aşamalı örnekleme
Çok aşamalı örnekleme küme örneklemesinin biraz daha karmaşık bir şeklidir. Küme örneklemesi için basit rastgele örnek olarak seçilmiş kümeler gerekmekte ve seçilen kümeler içinde tam sayım yapılması önerilmektedir. Bu tam sayım (ya parasal veya diğer kaynak kullanımına göre) çok maliyetli ve hatta imkânsız bile olabilir. İki aşamalı örneklem için birinci aşamada (aynı küme örneklemesi gibi) basit rastgele örnekleme ile belirli sayıda küme seçilir. Bundan sonra ikinci aşamada kullanılan çerçeveler ilk aşamada seçilmiş kümeler olur. Her seçilmiş küme için basit rastgele örnekleme uygulanıp tüm küme hacminden daha ufak sayıda örnekleme girecek elemanlar seçilir. Nadir hallerde ikiden fazla aşama da uygulanabilir. Bunda ilk aşama küme seçmektir; ondan sonraki aşama veya aşamalarda gittikçe birbiri içine girmiş alt-küme, alt-alt-küme vb. seçmek amaçtır ve en son aşamada ise seçilmiş alt-alt..-küme içinden basit rastgele örnek seçilir. Bu son aşamada elde edilecek örnek büyüklüğünün kaç eleman kapsayacağı kararı önemlidir. Eğer örnek büyüklüğü ile anakütledeki küme (veya alt-alt-..-küme oranında eşitlik istenirse herhangi bir seçilen küme içinde bulunan tüm anakütleye orantılı eleman sayısı son aşama örnek büyüklüğü seçiminde de aynen uygulanır.
Eşli rastgele örnekleme
'Eşli rastgele örnekleme birbirine bağlantısı olan iki değişik örneğe elaman seçimini kapsar. Anakütle elamanları önce diğer bir karakteristiğe veya değişkene göre eşlenerek o değişkeni inceleyecek örneklere seçilmiş olurlar. İnceleme yapılacak diğer bir karakteristik veya değişken için kullanılacak bu önceden eşlenmiş elamanları nasıl rastgele bu yeni değişken için örneklere tahsis edileceği eşli rastgele örnekleme yöntemi kullanılarak yapılır.
Bu çeşit olasılık örneklemi bulmak özellikle şu iki halde çok uygundur:
- Araştırıcı birbirine doğal veya diğer özel karaktere göre eşli olan elemanları bulmuştur. Bu eşli elamanlar yeni bir araştırma sorunu incelemek için örneklenmeleri eşli rastgele örnekleme yöntemi ile yapılır. Örneğin önceden bulunan iki örneklemeden birine bir özdeş ikiz ve diğerine öbür ikiz tahsis edilmiştir. Yeni incelenecek sorun zeka testi sonuçlarıdır. Eşli rastgele örnekleme' yöntemi ile daha önceden iki örnekleme ayrılan özdeş ikizler için yeni bir örnek bulması yöntemidir.
- Bir vasıf veya değişkene göre örnek elemanları üzerine iki defa ölçüm uygulanır; ikinci uygulama birinci örneğe özel bir sağaltım uyguladıktan sonra yapılır. Bu çeşit ölçüme tekrarlanan ölçümler adı verilir. İkinci ölçüm için örnek seçimi eşli rastgele örnekleme yöntemine göre yapılır. Örneğin, bir grup 1500m koşucusuna özel bir antrenman usulu tatbik etmeden önce ve ettikten sonra elde edilen koşu zamanı ölçümleri.
Formel matematiksel rastgele örneklem seçme tanımı
Matematik olarak rastgele örnekleme daha formel bir şekilde tanımlanır. X olasılık dağılımı F olan verilmiş bir rassal değişken olsun. n=1, 2,3,... büyüklüğü olan bir rastgele örnek F dağılımı olan n tane bağımsız ve her biri ayni şekilde dağılım gösteren n elemanı bulunan bir settir.
Bir örnek somut şekilde, her bir denemede aynı miktar ölçülürse n tane denemeyi temsil eder. Örneğin, biz üniversite öğrencilerini boyu ile ilgili isek X bir öğrencinin boyu olur ve 
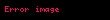
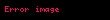

Böylece matematik açıklamaya göre örnek kavramı verilerin (yani rassal değişkenlerin) nasıl elde edilmeleri sürecini açıklamaktadır. Bu gereklidir çünkü örnek ve bundan elde edilen hakkında matematik ifadelerin verilmesi gerekmektedir.
Kaynakça
- ^ D.Huff, [1993] How to lie with statistics, W.W.Norton & co.
- ^ Burada istatistik bilimine ait özel terimler kullanılmaktadır. Bu istatistik bilimi terimleri "ISI (Uluslararası İstatistik Enstitüsü) tarafından hazırlanmış aralarında Türkçe de bulunan 31 dilde karşılıklı olarak "Çoklu Dilli İstatistik Terimleri Lugati (ISI Multilingual Glossary of Statistical Terms)" adlı bilimsel eserde kabul edilmiştir. [1] 8 Şubat 2016 tarihinde Wayback Machine sitesinde .
- ^ Wilk, Samuel S. (1962), Mathematical Statistics, John Wiley, Bol.8.1
Ayrıca bakınız
Dış bağlantılar
- İstatistik terimlerinin basit olarak açıklanması 23 Şubat 2008 tarihinde Wayback Machine sitesinde . (İngilizce)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddedeki bilgilerin dogrulanabilmesi icin ek kaynaklar gerekli Lutfen guvenilir kaynaklar ekleyerek maddenin gelistirilmesine yardimci olun Kaynaksiz icerik itiraz konusu olabilir ve kaldirilabilir Kaynak ara Ornekleme istatistik haber gazete kitap akademik JSTOR Aralik 2022 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Ornekleme istatistikte belirli bir yigindan alinan kumeyi ifade eder Ornegin Turkiye deki tum universite sayilari bir yigin iken Ankara daki universite sayisi bu yigindan alinmis bir ornektir Ornek hesaplamalarinda n displaystyle n x displaystyle bar x s2 displaystyle s 2 s displaystyle s p displaystyle p gibi semboller kullanilirken yigin hesaplamalarinda ise bu simgelerin yerine sirasi ile N displaystyle N m displaystyle mu s2 displaystyle sigma 2 s displaystyle sigma p displaystyle pi simgeleri kullanilir Istatistik sadece ornekler uzerinde hesaplanabilir Yiginda ise parametre degerleri hesaplanir Istatistik bilim dalinda ornekleme N hacimli bir anakutleden anakutleyi temsil edebilen n hacimli bir altkume elde edilmesidir Tipik olarak anakutle cok buyuktur veya tum anakutle elemanlari hakkinda bilgiler elde etmek imkansizdir veya elde etmek icin anakutleyi degistirmek veya elemanlarina zarar vermek gerekecektir veya cok buyuk masraf ve emek gerektirecektir Bu nedenle ile tum sayisal degerlerin ogrenilmesi istenmez Ornekleme ile kullanilabilir bir buyuklukte altkume elde edilir Ornek verileri toplanir ornek verileri hakkinda istatistikler hesaplanir ve ornek istatistikleri uzerinde cikarimsal istatistik veya ekstrapolasyonlar kullanarak anakutle hakkinda bilgiler elde edilir Ornegin Turkiye de universite ogrencilerinin fen bilimleri hakkindaki tavirlari olculmek istensin ve bu tavirlari aciklayan 10 soruluk bir anket hazirlanabilecegi bilinsin Turkiye de 2006 2007 ogretim yilinda universite ogrencisi olanlarin tumunun bu 10 soruya sayisal sekilde yanit verdigi varsayilsin Her bir soruya verilen yanitin sayisal degerlerinin tumu birer anakutle olur Burada dikkat edilecek nokta istatistik bilimi icin anakutlenin sayisal degerler olmasi ve universite ogrencisi olmamasidir Universite ogrencilerinin hepsi anakutle cercevesi olarak anilir Bu turlu sonuc bulmak ya imkansizdir ya da buyuk emek para ve zaman istemektedir Bu nedenle ornekleme metodunun uygulanmasi tercih edilir Bu anakutlenin orneklemini elde etmek icin anakutle cercevesi olan 2006 2007 ogretim yilinda Turkiye deki universitelerde okuyanlardan kucuk bir grup secilir Bu daha kucuk grup elemanlarina ornekleme cercevesi adi verilir Eger her universiteden uygun bir sayida ogrenci cesitli kullanarak secilirse bunlarin tumu ornekleme cercevesini olusturur Yine ornegi aciklamaya devam edersek bu daha nispeten kucuk gruba dikkat edilirse orneginde verilen ornekleme cercevesi yine de sayica kucuk olmaz bu hazirlanmis on soruluk anket uygulanir Her 10 soruya bu kucuk grup elemanlarinin verdigi sayisal yanitlar birer ornekleme olur Ornek ornekleme cercevesi uzerinde belirlenmis bir degisken uzerinde yapilan sayim veya olcum ile elde edilen sayisal verilerdir Tekrar dikkat cekilmelidir ki istatistik bilimi icin ornek kavrami ozel bir sekildedir ve genelde kullanilan ornek sozcugu anlamindan degisiktir Istatistik icin ornekleme cercevesi elamanlari bu ornekte secilen universite ogrencileri ornegi olusturmazlar her ornek cercevesi elemanindan bir degisken hakkinda elde edilen sayisal veriler bu ornekte her bir 10 soruya verilen sayisal yanitlar ornek olustururlar Ornekleme teknikleriGenel ornekleme teknigi tanimi Yukarida anakutle cercevesinden uygun bir sekilde bir daha ufak ornekleme cercevesi elde edilir denilmisti iste bu uygun sekillerin incelenmesi ornekleme tekniklerinin incelenmesi demektir Genel olarak ornekleme cercevesinin anakutle cercevesinden elde edilmesi icin prensip ornekleme cercevesinin anakutleyi temsil edici olmasidir Ornek verileri bir art fikirle bazi kisisel veya grupsal fikir ve prensiplere guya bilimsel bir destek saglamak icin kullanilmamasi gerekmektedir ama ne yaziktir ki pratikte bircok ticari sinai sosyal ve politik ornek bu niyetle elde edilip kullanilmakta ve genel gercekte temsilci olma prensibinden uzaklasilmaktadir Bu istatistikle yalan soyleme seklinde adlandirilabilen bircok arastirmalarda ele alinan bir konu olmustur Eger temsilci olma prensibine uygunluk arzu edilmekte ise ornekleme teknigi secimi icin iki genel teknik grubu bulunmaktadir Istatistiksel olasilik prensiplerine dayanmayan teknikler ve Istatistik olasilik prensiplerine dayanan rastgele ornekleme teknikleri Bu kavramsal ayrimi saglayan prensip olasilik prensipleridir ve bu prensiplere uyan ornekler rastgele ornek adi ile anilmaktadir Rastgele ornek icin kullanilan prensip genel olarak anakutle cercevesi icinde bulunan her elemanin ornek cercevesi icine alinma olasiliginin onceden belirlenmis bir olasilik dagilimina gore olmasidir Fakat genel olarak secilen olasilik dagilimi Bernoulli dagilimi oldugu icin bircok referansta bu prensip anakutle cercevesi icinde bulunan her elemanin ornek cercevesi icine alinma olasiliginin esit ve ayni olmasidir seklinde ifade edilmektedir Dikkat edilirse rastgele ornek icin temsilcilik prensibi ozel olarak matematik istatistik icerigine gore degistirilmistir belirlenmis bir dagilima gore olasilik esit olasilik prensibi on plana alinmistir Eger anakutle elemanlari icin bu prensip uygulanirsa bunun mantiksal olarak temsilcilik prensibine uyacagi da ima edilmektedir Burada bu iki grup ornekleme teknigine ait olan teknikler genel olarak detaya inmeden aciklanacaktir Olasilik prensiplerine uymayan ornekleme teknikleriElverislilik ornegi Elverislilik ornegi metodunda ornek cercevesine girecek anakutle elemanlari arastirmayi yapanin keyfine gore plansiz tasarimsiz secilir Ornek seciminde onemi olan prensip elde edilen ornegin istatistik arastirmayi yapan kisi icin elverisli olmasidir Eger arastirmaci bilincli inanilir ve guvenilir bir kisi ise ornekin anakutlenin temsilcisi olma imkani vardir ama bunun gercekte gecerli olup olmadigini kontrol edecek hicbir alet veya kural ortada bulunmamaktadir Bu cesit ornekleme daha sonra bir rastgele ornek almak icin bir pilot calisma icin kullanilmasi cok kere tavsiye edilmektedir Mekanik ornekleme Laboratuvarlarda fabrikalarda ve diger uretim kurumlarinda test ve kontrol maksadi ile kati maddeler sivilar veya gazlar mekanik arac ve gerecler kullanilarak orneklem alinir Ozellikle kalite kontrolu surecinde ve diger testler ve kontrollar icin bu mekanik orneklerin anakutlelerinin temsilcisi olmasi gerekmektedir Yargisal ornekleme Yargisal ornekleme bir uzman kisi veya bilirkisinin kendi ozel bilgisini ve yargisini kullanarak temsilci olma niceligini tasiyan elemanlar ile bir ornekleme cercevesi kurmasidir Bu cesit orneklerde cok kere bilinmeyen ve daha onceden hic tahmin edilme imkani olmayan yanliliklar ortaya cikar Ornek secme usulu ve protokollerinin kurulusu ve kullanisi sirasinda seffaflik olmadigi icin bilinmezliklerin nerede ve nasil ortaya cikabilecekleri ve nasil yanliliklarin aksi tesirlerinin nasil carelerle giderilebilecegi bilinmez Bazi hallerde yargisal ornekleme kullanisli ve hatta tercih edilir ornek alma teknigi olabilir Rastgele orneklemenin imkansiz veya cok buyuk zaman emek ve para sarfi gerektirdigi icin kullanissiz oldugu hallerde yargisal ornekleme gayeye uygun veriler ortaya cikartabilir Diger bir uygun olma hali eger kullanilacak ornek cok kucuk ise 10 veya daha asagi sayida veri ongoruluyorsa bir rastgele orneke nazaran bir yargisal ornek bulmak daha guvenilir ve daha iyi temsilci olma ozelligi tasiyan bir orneklem ortaya cikartabilir Bazen kasten hic temsilci olmayan ve gayet yanli bir ornek kasten secilmek istenebilir ve bu halde yargisal ornek tercih edilir Bu kasten yanli olarak yargisal ornek secimi arastirma konusunun en fena alternatif halini incelemek icin cok uygundur Kota ornegi Bu cesit orneklemede anakutlede tabakalar bulundugu ve bu tabakalara ait olan elemanlarin birbirlerine cok benzer ozellikler gosterdigi fakat degisik tabakaya mensup elemanlarin ozelliklerinden acikca farkli olduklari bilinmektedir Arastirmaci once bu tabakalarin ozelliklerini tam olarak saptar ve degisik tabakalari birbirinden ayirt eden ozellikleri tespit eder Cok kere bu tabakalari ayirt edici ozellikler kisilerin sosyo demografik ozellikleri olur Buraya kadar yapilan islemler aynen olasilik prensibine uyan tabakali orneklemede de uygulanir Ikinci adim olarak kota orneklemede her veri toplayicisina tespit edilmis her tabaka icin aldiklari ornekte cok kere anket sorularini cevaplandirici sayisi olan kac gozlem ile bulunacagini tespit eden bir kota sayisi verilir Bundan sonra veri toplayicilar kendilerine verilen her tabaka icin kota sayisina gore kendi sahsi yargilarini kullanarak veri toplarlar Bu adim tipki bir yargisal ornekleme gibidir ama yargiyi uygulayanlar cok defa uzman kisi veya bilirkisiler degil gercek veri toplayicilardir Kartopu orneklemesi Bu orneklemede once bir cekirdek orneklem elverislilik ornegi gibi arastirmayi yapan tarafindan kendi keyfine gore bulunur Ondan sonraki orneklem elemanlari ise daha once bulunmus olan cekirdek elemanlar ve onlarin sectigi diger elemanlar tarafindan bulunurlar Ornek boylece sanki karda itilerek buyuyen bir kartopu gibi buyume gosterir Rastgele orneklemeRastgele ornekleme olasilik orneklemesi olarak da adlandirilir Rastgele ornek bulma ve kullanma icin istenilen ozellik Her bir anakutle elemaninin belirli olasilikla ornekte bulunmasidir Bundan aciktir ki istenilen ozellik dogrudan dogruya ornegin anakutle icin temsilci olmasi degildir Temsilci olma prensibine rastgele ornekleme biraz dolayli olarak varmaktadir Rastgele ornekleme kavrami ve prensibi temsilci olmama riskini bir seri istatistik teori kavrami ile niceliksel olarak aciga cikarmaya yoneliktir Bu niceliksel sonuclar once hangi cesit rastgele orneklemenin secilmesi ve sonra ne kadar buyuk bir ornek hacmi elde edilmesi gerektigine karar vermekte kullanilir Bu ornek alinmasindan once karar verme yaninda ornek alindiktan sonra olculmus sonuclara bagli ornekleme hatasini hesaplamaya yardim saglar Belirli olasilik teriminin tanimlanmasina gore degisik turlu rastgele ornek ortaya cikabilir Bunlardan en iyi bilineni basit rastgele orneklemedir Bu turlu orneklemenin ana prensibi her bir anakutle elemaninin ayni olasilikla ornekleme girebilmesidir Yani her bir anakutle elemani icin ornekte bulunma olasiligi bir Bernoulli dagilimi gosterir Diger turlu belirli olasilik her bir anakutle elemaninin Poisson dagilimina gore birbirine esit olmayarak ornek icinde bulunmasidir Ancak rastgele orneklemeler icin siniflandirma gosterilen olasilik dagilimina gore yapilmamakta daha pratik olarak nasil rastgele olmanin saglanma yontemine dayanilmaktadir Bu siniflandirmaya gore rastgele ornekleme sinifi icinde su degisik ornekleme tipi mevcuttur Basit rastgele ornekleme Oruntulu ornekleme Tabakali ornekleme Kume orneklemesi Cok asamali ornekleme Esli rastgele orneklemeBasit rastgele ornekleme Basit rastgele orneklem almanin ana prensibi her bir anakutle elemaninin ayni olasilikla ornege girebilmesidir Bu bir olasilik ornegi tanimina uyar cunku her bir anakutle elemani icin orneklemde bulunma olasiligi bir Bernoulli dagilimi gosterir Eger anakutle buyuklugu N ile ifade edilirse her bir anakutle elemani 1 N olasilikla ornekte bulunur Bu prensibi uygulamak icin su asamalar uygulanir Anakutlenin her bir elemani tespit edilir ve tespit edilen elamanlarin her birine bir sayisal kod verilir Genellikle kodlar birbirini takip eden sayilar halinde siralama duzeni halindedir ve sanki sayisal bir isimdir Ikinci asamada en uygun orneklem hacmi yani n tayin edilir Bir rastgele numara uretici alet kullanilarak istenilen n sayida birbirinden degisik olmasi tercih edilir rastgele sayi cikartilir Rassal sayilar gayet cok oldugu icin bir cesit geri koymadan ornek alma deneyim sonucu olan n tane rastgele sayi ayni olasiliga haizdir Bu rastgele n numara anakutle elemanlarinin kodlari ile karsilastirilir Kod numarasi cekilmis olan rastgele sayiya esit olan elemanlar ornek elemani olarak secilirler Oruntulu ornekleme Bu olasilik ornekleme yontemin ana prensibi bir icinde bulunan her bir elemana sira bir kod numarasi verilebilirse rastgele secilmis veya hesaplama ile bulunmus bir kod araligi olan k araligi ile her kinci elemanin gozlem yapilacak ornekleme secimidir Ornegin belli bir universitede kayitli ogrenci numaralari belli bir numaradan baslayip giden bir siraya tabi iseler ilk olarak bir rastgele kayit numarasi secilir ve sonra bir rastgele aralik numarasi secilir diyelim 54 baslangic kayit numarasi ve 12 de kod araligi rastgele secilmis olsun Oruntulu orneklemede ornege dahil edilecek ogrenci elamanlarin su kayit numaralari olmalidir 54 66 78 90 onceden secilmis n tane orneklem hacmi elde edilinceye kadar Tabakali ornekleme Bu cesit olasilik ornekleme yonteminde anakutlenin tabakalardan olustugu gercegi kabul edilmektedir Her tabaka elemani bir veya bir grup teshis edici degisken degeri dolayisiyla birbirlerine cok benzedikleri kabul edilirler Bu cesit teshis edici degisken ler icin degerler tabakalar arasinda cok farklidir Bircok sosyal bilim arastirmasi icin bu teshis edici degisken bir veya birkac sahsi veya ekonomik veya sosyal ozelliklerden olusur Ornegin temsilcilik prensibine uymasi icin anakutlenin her bir tabakasindan degisik sayida ornek secilir ve ornek de ayni anakutle gibi tabakali olur Genel olarak her anakutle tabakasi ve ornek tabakasi elemanlari arasinda iliski kurulabilir Orantili tabakalar denilebilen bir tipe gore anakutle icinde her bir tabakanin toplama orani ornek tabakasinin ornek buyukluk hacmine orani ile aynidir Bu oran en populer olarak tabaka icindeki teshis edici degisiklik karakteri tasiyan elemanlarin sayisi ile toplam orantilidir Diger bir alternatif standart sapmalarin orani olabilir Diger alternatifte orantisiz tabakalar adi verilir ve daha baska yargisal secimlerle ornek tabaka elemanlari anakutle tabakalarina temsilci olmasi saglanir Kume orneklemesi Bu sekilde ornekleme genellikle ornekleme zaman ve para maliyetlerini dusuk tutmak icin kullanilmaktadir Anakutle cercevesi elamanlarinin birbirine yakin kumeler olusturdugu hallerde ve her bir kume genel olarak diger kumelere cok benzerlerse bu tipi ornekleme kullanilmasi uygun olabilir Ornegin anakutle cercevesi belli bir universite olursa o universite icindeki degisik bolumlerde bulunan ogrencilerin benzer ozellikler gosterdikleri kabul edilebilir ve bolumler incelenen sorun icin birbirinden cok degisik degillerse bolumler birer kume olarak incelemeye taban olabilirler Bu kumeler mekan icinde ornegin sehrin degisik mahalleleri veya Amerika daki gibi degisik sehir bloklari veya zaman icinde belirli zaman donemleri olabilir Kume orneklemesi iki asamada yapilir Birinci asamada cok iyi belirlenmis kumeler tespit edilir Her iyi belirlenmis kumeye bir kod numarasi verilir Butun kod numaralari icinden basit rastgele ornekleme ile kucuk sayida kumeler ornegi secilir Ornegin bir universite 35 tane bolumden olusmussa ve her bolume ait ogrenci uyeler iyice tespit edilmislerse her bir bolum kodlanir ve diyelim 8 tane bolum bu 35 bolumden basit rastgele ornek olarak yani 35 bolum de ornege dahil olmak icin ayni olasiligi tasiyarak secilirler Ikinci asamada her bir ornege giren kume icinde bulunan butun anakutle elemanlari uzerinde gozlem yapilir Yani her ornek kume icin tam sayim yapilir Ornegin ilk asamada secilmis olan 8 bolumdeki her ogrenci elemanlarinin tumune gozlem uygulanir Dogal olarak tum anakutle cercevesi secilmedigi icin zaman ve para maliyetleri tam sayimdan dusuk olur Dikkat edilirse bu cesit orneklemede rastgele secilme kumelerle ilgilidir Bu secim yapildiktan sonra secilen kumeler icinde bulunan birbirine yakin elemanlar gozumlendigi icin de maliyetler ozellikle basit rastgele orneklemeye kiyasla daha dusuk olmasi cok mumkundur Basit rastgele orneklemeye kiyasla kume orneklemesinin bir diger avantaji tum anakutle elemanlarinin her birinin kodlanmasinin gerekmedigidir bu tum kodlama buyuk maliyet gerektirir ve bazen de imkansizdir Buna karsilik kume orneklemesinde sadece birinci asamada secilmis olan kumeler elemanlari tespit edilip kodlanir Ancak kume orneklemesi her bir kumenin diger kumelere benzedigine ve sadece kendine has karakteri olan bir veya birkac kumenin bulunmadigi varsayimina dayanir Gercekte bu varsayim her zaman ancak yaklasik olarak dogru olacak ve bazi belirlenen kumeler kendine has karakter arz edecektir Bu nedenle kume orneklemesinin yayilimi ayni anakutle icin alinabilecek basit rastgele orneklemeden daha fazla olacaktir ve orneklemeden sonra elde edilecek kestirimler veya yapilan sinamalar daha az tutarli olacak ve daha fazla yanli olma olasiligi tasiyacaklardir Cok asamali ornekleme Cok asamali ornekleme kume orneklemesinin biraz daha karmasik bir seklidir Kume orneklemesi icin basit rastgele ornek olarak secilmis kumeler gerekmekte ve secilen kumeler icinde tam sayim yapilmasi onerilmektedir Bu tam sayim ya parasal veya diger kaynak kullanimina gore cok maliyetli ve hatta imkansiz bile olabilir Iki asamali orneklem icin birinci asamada ayni kume orneklemesi gibi basit rastgele ornekleme ile belirli sayida kume secilir Bundan sonra ikinci asamada kullanilan cerceveler ilk asamada secilmis kumeler olur Her secilmis kume icin basit rastgele ornekleme uygulanip tum kume hacminden daha ufak sayida ornekleme girecek elemanlar secilir Nadir hallerde ikiden fazla asama da uygulanabilir Bunda ilk asama kume secmektir ondan sonraki asama veya asamalarda gittikce birbiri icine girmis alt kume alt alt kume vb secmek amactir ve en son asamada ise secilmis alt alt kume icinden basit rastgele ornek secilir Bu son asamada elde edilecek ornek buyuklugunun kac eleman kapsayacagi karari onemlidir Eger ornek buyuklugu ile anakutledeki kume veya alt alt kume oraninda esitlik istenirse herhangi bir secilen kume icinde bulunan tum anakutleye orantili eleman sayisi son asama ornek buyuklugu seciminde de aynen uygulanir Esli rastgele ornekleme Esli rastgele ornekleme birbirine baglantisi olan iki degisik ornege elaman secimini kapsar Anakutle elamanlari once diger bir karakteristige veya degiskene gore eslenerek o degiskeni inceleyecek orneklere secilmis olurlar Inceleme yapilacak diger bir karakteristik veya degisken icin kullanilacak bu onceden eslenmis elamanlari nasil rastgele bu yeni degisken icin orneklere tahsis edilecegi esli rastgele ornekleme yontemi kullanilarak yapilir Bu cesit olasilik orneklemi bulmak ozellikle su iki halde cok uygundur Arastirici birbirine dogal veya diger ozel karaktere gore esli olan elemanlari bulmustur Bu esli elamanlar yeni bir arastirma sorunu incelemek icin orneklenmeleri esli rastgele ornekleme yontemi ile yapilir Ornegin onceden bulunan iki orneklemeden birine bir ozdes ikiz ve digerine obur ikiz tahsis edilmistir Yeni incelenecek sorun zeka testi sonuclaridir Esli rastgele ornekleme yontemi ile daha onceden iki ornekleme ayrilan ozdes ikizler icin yeni bir ornek bulmasi yontemidir Bir vasif veya degiskene gore ornek elemanlari uzerine iki defa olcum uygulanir ikinci uygulama birinci ornege ozel bir sagaltim uyguladiktan sonra yapilir Bu cesit olcume tekrarlanan olcumler adi verilir Ikinci olcum icin ornek secimi esli rastgele ornekleme yontemine gore yapilir Ornegin bir grup 1500m kosucusuna ozel bir antrenman usulu tatbik etmeden once ve ettikten sonra elde edilen kosu zamani olcumleri Formel matematiksel rastgele orneklem secme tanimiMatematik olarak rastgele ornekleme daha formel bir sekilde tanimlanir X olasilik dagilimi F olan verilmis bir rassal degisken olsun n 1 2 3 buyuklugu olan bir rastgele ornek F dagilimi olan n tane bagimsiz ve her biri ayni sekilde dagilim gosteren n elemani bulunan bir settir Bir ornek somut sekilde her bir denemede ayni miktar olculurse n tane denemeyi temsil eder Ornegin biz universite ogrencilerini boyu ile ilgili isek X bir ogrencinin boyu olur ve n displaystyle n tane ogrenci boyu olcumlenir ve Xi displaystyle X i i inci ogrencinin boyunu ifade eder Fakat bir sira olculebilir fonksiyondan olusan bir rassal degiskenler ornegi ile bu rassal degiskenlerin gerceklesmelerini yani rassal degiskenin almis oldugu degerleri kavramsal olarak ayri tutmak gerekmektedir Diger bir deyisle Xi displaystyle X i i inci denemedeki olcmeyi temsil eden bir fonksiyon olmakta ve xi Xi w displaystyle x i X i omega gercekte yapilan olcmelerden elde edilen sayilar olmaktadir Boylece matematik aciklamaya gore ornek kavrami verilerin yani rassal degiskenlerin nasil elde edilmeleri surecini aciklamaktadir Bu gereklidir cunku ornek ve bundan elde edilen hakkinda matematik ifadelerin verilmesi gerekmektedir Kaynakca D Huff 1993 How to lie with statistics W W Norton amp co Burada istatistik bilimine ait ozel terimler kullanilmaktadir Bu istatistik bilimi terimleri ISI Uluslararasi Istatistik Enstitusu tarafindan hazirlanmis aralarinda Turkce de bulunan 31 dilde karsilikli olarak Coklu Dilli Istatistik Terimleri Lugati ISI Multilingual Glossary of Statistical Terms adli bilimsel eserde kabul edilmistir 1 8 Subat 2016 tarihinde Wayback Machine sitesinde Wilk Samuel S 1962 Mathematical Statistics John Wiley Bol 8 1Ayrica bakinizDis baglantilarIstatistik terimlerinin basit olarak aciklanmasi 23 Subat 2008 tarihinde Wayback Machine sitesinde Ingilizce
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans