Alan Baker FRS (19 Ağustos 1939 - 4 Şubat 2018), sayı teorisindeki etkili yöntemler, özellikle de doğan konular üzerine yaptığı çalışmalarla tanınan İngiliz bir matematikçiydi.
Alan Baker | |
|---|---|
 | |
| Doğum | 19 Ağustos 1939 Londra, İngiltere |
| Ölüm | 04 Şubat 2018 (78 yaşında) Cambridge, İngiltere |
| Ölüm sebebi | serebrovasküler hastalık |
| Milliyet | İngiliz |
| Vatandaşlık | Birleşik Krallık |
| Eğitim | University College London Trinity College Cambridge Üniversitesi |
| Mezun olduğu okul(lar) | University of Cambridge |
| Tanınma nedeni | |
| Ödüller | Fields Madalyası (1970) (1972) Fellow of the American Mathematical Society Fellow of the Royal Society |
| Kariyeri | |
| Dalı | Matematik, Sayı teorisi |
| Çalıştığı kurum | University of Cambridge |
| Tez | Some Aspects of Diophantine Approximation (1964) |
| Doktora danışmanı | |
| Doktora öğrencileri | |
Hayatı

Alan Baker, 19 Ağustos 1939'da Londra'da doğdu. Doğu Londra'daki 'a katıldı ve akademik kariyeri, kazandığı Eyalet Bursu ile University College London'da 'un öğrencisi olarak başladı ve daha sonra Trinity College, Cambridge'de doktorasını Some Aspects of Diophantine Approximation (Diophantine Yaklaşımı'nın Bazı Yönleri) adlı teziyle aldı. 1961'de Matematikte Birinci Sınıf Şeref Ödülü'ne layık görüldü. Aslında, doktora tezini sunmadan önce sekiz makalesi basılmıştı:
- Aşkın sayıların sürekli kesirleri [Continued fractions of transcendental numbers] (1962);
- Mahler'in aşkın sayılar sınıflandırması üzerine [On Mahler's classification of transcendental numbers] (1964);
- Belirli cebirsel sayılara rasyonel yaklaşımlar [Rational approximations to certain algebraic numbers] (1964);
- Littlewood'un Diophantine yaklaşım probleminin bir benzeri üzerine [On an analogue of Littlewood's Diophantine approximation problem] (1964);
- Belirli rasyonel sayıların logaritmalarına yaklaşımlar [Approximations to the logarithms of certain rational numbers] (1964);
- 2 ve diğer cebirsel sayıların küp köküne rasyonel yaklaşımlar [Rational approximations to the cube root of 2 and other algebraic numbers] (1964);
- Cebirsel fonksiyonları temsil eden kuvvet serileri [Power series representing algebraic functions] (1965) ve
- Üstel işlevi içeren bazı Diophantine eşitsizlikleri üzerine [On some Diophantine inequalities involving the exponential function] (1965).
1965'te Trinity College Üyesi seçildi. 1964-65 akademik yılını University College London Matematik Bölümü'nde geçirdi.
Baker, 1964'ten 1968'e kadar Cambridge'de araştırma görevlisiydi, ardından 1968'den 1974'e Saf Matematik Profesörü olarak atandığı 1974'e kadar sürdürdüğü Matematik Çalışmaları Direktörü oldu. Cambridge'deki kariyeri boyunca Amerika Birleşik Devletleri'nde zaman geçirdi, 1970'te Princeton'daki İleri Çalışmalar Enstitüsü'nün bir üyesi ve 1974'te Stanford'da misafir profesör oldu. Aynı zamanda 1988'de Hong Kong Üniversitesi'nde, 1989'da Eidgenössische Technische Hochschule Zürich'te ve 1993'te Matematik Bilimleri Araştırma Enstitüsü, Berkeley, California'da misafir profesör oldu.
31 yaşında 1970 yılında Nice'deki Uluslararası Kongre'de Fields Madalyası ile ödüllendirildiğinde, 'de misafir araştırmacı olarak bulunuyordu. Bu ödülü, Diophantine denklemleri üzerindeki çalışması için aldı. Bu, tarihsel ortamı ilk veren Paul Turán tarafından aşağıdaki şekilde anlatılmıştır:
| “ | tarafından 1844'te başlatılan aşkın sayılar teorisi, son yıllarda büyük ölçüde zenginleşti. İlgili derin katkılar arasında Alan Baker, Wolfgang M. Schmidt ve Vladimir Gennadievich Sprindzuk'un katkıları bulunmaktadır. Çalışmaları, bağımsız değişkenin sıfır olmayan tüm cebirsel değerleri için aşkın değerler varsayan önemli fonksiyon sınıflarını bulma konusundaki geleneksel yoğunlaşma ile tezat oluşturan önemli yönlere doğru ilerliyor. Bunların arasında, matematikteki diğer problemler üzerinde en ağır etkiyi Baker'ın yaptığı görülmüştür. Belki de bu etkilerden en önemlisi Diophantine denklemlerine yapılan uygulama olmuştur. Bin yıldan daha uzun bir tarihe sahip olan bu teori, bu yüzyılın ilk yıllarına kadar, ustaca geçici yöntemlere tabi tutulmuş izole problemlerin bir koleksiyonundan biraz daha fazlasıydı. 1909'da 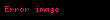 formundaki tüm Diophantine denklemlerini ispatlayarak genel sonuçlara atılım yapan kişi Axel Thue'du, burada formundaki tüm Diophantine denklemlerini ispatlayarak genel sonuçlara atılım yapan kişi Axel Thue'du, burada  bir tamsayıdır ve bir tamsayıdır ve  en az üç derecenin indirgenemez homojen ikili biçimi olup, tam sayı katsayıları ile tam sayılarda en fazla, sonlu çok sayıda çözüme sahiptir. en az üç derecenin indirgenemez homojen ikili biçimi olup, tam sayı katsayıları ile tam sayılarda en fazla, sonlu çok sayıda çözüme sahiptir. | „ |
Turán, Carl Siegel ve Klaus Roth'un, bu sonuçların tutacağı ve hatta çözüm sayısını sınırlayacağı Diophantine denklem sınıflarını genelleştirdiğini söylemeye devam ediyor. Baker daha da ileri gitti ve en azından prensipte bu tür problemlerin tam çözümüne yol açabilecek sonuçlar üretti. Yukarıda açıklanan 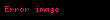



,
'nin herhangi bir
çözümü için
Elbette bu, yalnızca sınırlı sayıda olasılığın dikkate alınması gerektiği anlamına gelir, bu nedenle, en azından prensipte, sonlu olası çözümlerin her birini kontrol ederek çözümlerin tam listesi belirlenebilir.
1974'te Cambridge Üniversitesi'nde Saf Matematik Profesörü olarak atandı, 2006'da olana kadar bu pozisyonda kaldı. 1964'ten ölümüne kadar Trinity Koleji'nin bir üyesiydi.
Turán Baker hakkındaki sözlerini aşağıdaki şekilde bitiriyor:
| “ | [Baker'ın] çalışmalarının iki şeyi çok ikna edici bir şekilde örneklediğini belirtiyorum. Birincisi, bir problemi çözmek için bir teori başlatmaya layık eğilimin yanı sıra, belirli zor problemlere doğrudan saldırmak da işe yarar. ... İkinci olarak, derin bir problemin doğrudan çözümünün kendisini oldukça doğal bir şekilde sağlıklı bir teori haline getirdiğini ve matematiğin önemli problemleriyle erken ve verimli bir temasa geçtiğini gösterir. | „ |
Baker'ın ünlü kitapları arasında şunlar yer almaktadır: Aşkın sayı teorisi [Transcendental number theory] (1975), Aşkınlık teorisi: gelişmeler ve uygulamalar [Transcendence theory : advances and applications] (1977), Sayılar teorisine kısa bir giriş [A concise introduction to the theory of numbers] (1984), (Gisbert Wüstholz ile birlikte) Logaritmik formlar ve Diophantine geometrisi [Logarithmic forms and Diophantine geometry] (2007) ve Sayı Teorisinde Kapsamlı Bir Ders A Comprehensive Course in Number Theory] (2012). Transandantal sayı teorisine (1975) girişte Baker'ın aşağıdaki ifadesi yer almaktadır:
| “ | Aşkın sayıların incelenmesi ... şimdi matematiğin yaygın dallarını zenginleştiren verimli ve kapsamlı bir teori haline geldi. Amacım, bu alandaki son büyük keşiflerin kapsamlı bir hesabını sağlamaktı. Anlatım sırasında konunun klasik yönleri tartışılır. Konudaki ispatlar ... uzun ve karmaşık olma eğilimindedir ve bu nedenle ayrıntılı işlem için yalnızca en temel sonuçları seçmek gerekli olmuştur; dahası, genel olarak konuşmak gerekirse, bugüne kadar bilinen en güçlü önermelere yol açan veya en geniş uygulamayı sağlayan argümanlara vurgu yapılmıştır. | „ |
Robert Tijdeman bu kitabın bir incelemesinde şöyle yazıyor:
| “ | Yazar planında başarılı oldu. Bu kitap, aşkın sayı teorisinin önemli noktalarına, özellikle de yazarın 1970 yılında Fields madalyasıyla ödüllendirildiği kendi önemli katkılarına dair bir inceleme sunar. Aşkınlık teorisine genel bir bakış elde etmek isteyen matematikçiler için çok yararlı bir yayındır. teknikleri ve uygulanabilirliği. Tarz son derece yoğun, ancak daha ayrıntılı çalışma için birçok referans var. Sunum çok iyi yapılmış. | „ |
Bu kitap aynı zamanda Heini Halberstam (1926-2014) tarafından da incelenmiştir:
| “ | Yazar, sadece 130 sayfalık bir alan içinde, Adams Ödülü makalesine dayanarak modern aşkınlık teorisinin panoramik bir açıklamasını veriyor. Bunun artık "matematiğin geniş dallarını zenginleştiren verimli ve kapsamlı bir teori" olduğu gerçeği, büyük ölçüde, katkılarından dolayı 1970 yılında Fields Madalyası (Nobel matematik Ödülü) ile ödüllendirilen yazarın kendisine bağlıdır. Düz yazı net ve ekonomiktir, ancak bir kişilik duygusu yansıtan renk parlamaları ile serpiştirilmiştir; ve her bölüm, sonraki konunun yararlı bir özetiyle başlar. Tüm aşamalardaki matematiksel argüman oldukça yoğunlaştırılmıştır, çünkü aslında bu kadar çok zemini kapsayan kısa bir araştırma monografisinde kaçınılmazdır. Yeni başlayanlara daha merhametli davranmadığı için yazarı kınayabilir; ancak yeni başlayan biri bile kitaptan, bu son derece zor alanda bugüne kadarki en büyük başarıların neler olduğu ve önemli sorunların neler olduğu konusunda net bir izlenim edinebilirken, diğerleri için burada çok sayıda verimli çalışma grubu için bol miktarda materyal bulunmaktadır. | „ |
Baker'ın 1984 tarihli "Kısa Giriş (Concise Introduction)" yazısını inceleyen Don Redmond şöyle yazar:
| “ | Pek çok kitap adlarına uymaz, ancak bu kesinlikle adına uyan bir kitaptır. Kitap çok özlü ve standart bir dersin temel noktalarını kapsadığı için güzel bir referans olabilir, ancak eleştirmen onu sayı teorisindeki ilk dersin tek ders kitabı olarak kullanabileceğinden emin değildir. | „ |
"Kısa Giriş"i de inceleyen David Singmaster şöyle yazıyor:
| “ | Sayı teorisine giriş konusundaki çalışmalar çok sayıdadır, bu nedenle herhangi bir yeni çalışma, yenilik açısından incelenmelidir. Bu kitap, Cambridge Üniversitesi'nde bir dersi için ders materyaldir. Sonuç olarak, "özlü" abartı değildir. ... Genel olarak, kitap bir yoğunlaşma harikasıdır. Bu, 91 sayfalık metnin tamamı ana materyale ayrılmış olsa bile doğru olacaktır, ancak kendisi daha da yoğunlaştırmış ve ek materyali için yaklaşık 30 sayfa kullanmıştır. Bu, gördüğüm mevcut sayı teorisinin en kullanışlı özetini içerir. Yetkili bir indeks var, böylece sonuçların yeri belirlenebilir. ... Bu kitabı, alanla ilgili bir araştırma yapmak isteyen herhangi ciddi bir lisans öğrencisine tavsiye ederim, ancak kanıtların çok dikkatli olması gerektiği konusunda onu uyarırım. Sayı teorisinde bir geçmişi olan herkes, Baker'ın mevcut bilgi açıklamasını çok beğenecektir. | „ |
Yuri Bilu, Baker ve Wüstholz'un 2007 tarihli Logaritmik formlar ve Diofantin geometrisi kitabının bir incelemesinde şunları ifade etmektedir:
| “ | Uzun zamandır beklenen bu kitap, Baker, Masser ve Wüstholz'un hem lisans hem de lisansüstü öğrencilerine uygun bir biçimde klasik çalışmalarına giriş niteliğindedir. ... Bu kitap gerçekten bir giriş niteliğindedir. Amacı teknik özelliklerden kaçınırken ilkeleri öğretmektir. Bu, içeriğe belirli sınırlamalar getirir. Yazarlar, çarpımsal grup için nitel teoriyi çok ayrıntılı olarak ele alırlar, ancak nicel açıdan fazla bir şey söylemezler ve sadece kısaca değişmeli çeşitlerden söz ederler. Bununla birlikte, bu kitap, Baker, Masser, Wüstholz ve diğerlerinin yukarıda sıralanan konularda orijinal dergi makalelerini incelemek için gerekli sezgisel arka planı sağlar. | „ |
Baker ayrıca aşkınlık teorisindeki (1988) önemli Yeni gelişmeleri düzenledi ve Gisbert Wüstholz ile önümüzdeki bin yılda Sayı teorisi, aşkınlık ve Diophantine geometrisi başlıklı önemli çalışmayı yazdı. Bu, aşkınlık teorisi ve ilgili matematikteki başarıların ve açık problemlerin bir araştırmasıdır.
1999'da, Baker'ın 60. doğum gününü kutlamak için Zürih'te bir konferans düzenlendi. Toplantılarda verilen derslerin çoğu A Panorama in Number Theory or The View from Baker's Garden (2002) adlı eserde yayınlandı. Kitaba giriş şu şekilde başlıyor:
| “ | Alan Baker'ın 60. doğum günü ile birlikte milenyum, sayı teorisinde bir toplantı düzenlemek ve bu alandaki önde gelen uluslararası araştırmacılardan oluşan bir grubu bir araya getirmek için tekil bir fırsat sundu; Forschungsinstitut für Mathematik ile birlikte ETH Zürich tarafından cömertçe desteklendi. Bu, bizi büyük bir sayı teorisi yelpazesini ve ilgili geometriyi özellikle Diophantine yönlerine vurgu yaparak kapsamayı amaçlayan bir program geliştirmeye teşvik etti. ... Londra Matematik Derneği, Başkanı Profesör Martin Taylor tarafından temsil edildi ve 60. doğum günü vesilesiyle Alan Baker'a selamlar gönderdi. | „ |
Baker, sayı teorisinin tarihi, özellikle de aşkın sayılar üzerine açıklamalar yapar:
| “ | Peki, bu bize matematiğin tarihsel evrimi hakkında ne söylüyor? Birincisi, Profesör Dieudonné'nin terminolojisinde birkaç anahtar sorunun, çekim merkezlerinin çok önemli bir rol oynadığı açıktır. Bu sayı teorisi için diğer matematiğin dallarından daha doğru olabilir, ancak tüm iyi çalışmaların bir dereceye kadar bu tür merkezler tarafından yönlendirildiğine inanıyorum. Tartışmakta olduğum belirli alanın genel eğilimini özetlemek zordur, çünkü gelişiminde pek çok yeni kıvrımlar ve dönüşler yer almıştır; ancak evrimdeki açık bir unsur, sayı teorisi ve cebirden gelen fikirlerin klasik fonksiyon teorisinin giderek daha geniş kullanımıyla başarılı bir şekilde harmanlanması veya birleştirilmesidir. Ve inanıyorum ki, aktif bir teorinin yaratılmasında temel bileşeni oluşturan çeşitli kavramların bu yakınsamasıdır. Profesör Dieudonné'ye göre, aşkın sayıların incelenmesi, sadece bir "yöntem" olma yolundadır. Bununla birlikte, çözmede aracı olduğu problemlerin çeşitli doğası göz önüne alındığında, son aşamaya birkaç yıl önce ulaştığına dair çok az şüphe var gibi görünüyor ve aslında bu, halihazırda Profesör Dieudonné'nin dilinde, bir çekim merkezi olma yolunda olduğu ortaya çıkıyor. | „ |
Baker'ın Cambridge Üniversitesi sayfasında verilen araştırma ilgi alanları (Ocak 2014'te derlenmiştir):
| “ | Cebirsel sayıların logaritmalarının doğrusal bağımsızlığına dair Baker Teoremi, son otuz yılda sayı teorisindeki çok çeşitli gelişmelerin anahtarı olmuştur. Bunların en önemlileri, Diofantin denklemlerinin etkili çözümüne, sınıf numarası problemlerinin çözümüne, p-sel L-fonksiyonları teorisine ve özellikle Masser ve Wüstholz'un çalışmaları aracılığıyla aritmetik cebirsel geometrinin birçok derin yönüne yapılan uygulamalardır. Teori, günümüze kadar çok verimli araştırma kaynağı olmaya devam ediyor. | „ |
Ayrıca genel ilgi alanları sayı teorisi, , , , ve Diophantine analiziydi.
Baker matematiğin dışında ilgi alanlarını seyahat, fotoğraf ve tiyatro olarak sıralıyor.
Başarıları
Baker ayrıca a ve q cebirsel olduğunda 
| “ | ... geniş bir genellemesini elde etmeyi başardı. Bu çalışmadan, daha önce tanımlanmamış büyük bir aşkın sayılar kategorisi oluşturdu ve temeldeki teorinin çok çeşitli Diophantine problemlerini çözmek için nasıl kullanılabileceğini gösterdi. | „ |
Baker, özellikle şunu gösterdi: 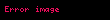


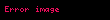
Baker, 1970 Fields madalyasına ek olarak matematiksel katkılarından dolayı birçok onursal ödül aldı. Bunlar arasında Cambridge Üniversitesi'nden Adams ödülü (1972) ve Royal Society of London seçimi (1973) yer alıyor. Université Louis Pasteur Strasbourg'dan (1998) fahri doktora unvanı aldı, University College London'da (1979) fahri bursiyeri, Hindistan Bilim Akademisi (1980), Hindistan Ulusal Bilimler Akademisi'nin yabancı bursiyeri (1993), Academia Europaea'nın (1998) bir üyesi ve Macar Bilimler Akademisi'nin (2001) onursal üyesidir.
2012'de American Mathematical Society'nin bir üyesi oldu. Ayrıca yabancı bir üyesi oldu.
Bazı yayınları
- Baker, Alan (1966), "Linear forms in the logarithms of algebraic numbers. I", , 13 (2), ss. 204-216, doi:10.1112/S0025579300003971, ISSN 0025-5793, MR 0220680
- Baker, Alan (1967a), "Linear forms in the logarithms of algebraic numbers. II", , cilt 14, ss. 102-107, doi:10.1112/S0025579300008068, ISSN 0025-5793, MR 0220680
- Baker, Alan (1967b), "Linear forms in the logarithms of algebraic numbers. III", , 14 (2), ss. 220-228, doi:10.1112/S0025579300003843, ISSN 0025-5793, MR 0220680
- Baker, Alan (1990), Transcendental number theory, Cambridge Mathematical Library (2. bas.), Cambridge University Press, ISBN , MR 0422171; 1st edition. 1975.
- Baker, Alan; Wüstholz, G. (2007), Logarithmic forms and Diophantine geometry, New Mathematical Monographs, 9, Cambridge University Press, ISBN , MR 2382891
- Baker, Alan. "A Concise Introduction to The Theory of Numbers" (PDF). Cambridge University Press. ISBN . 31 Mart 2020 tarihinde kaynağından (PDF). Erişim tarihi: 30 Ocak 2021.
Onurlandırılması ve ödülleri
- 1970: Fields Madalyası
- 1972:
- 1973: Kraliyet Cemiyeti Bursu
Notlar
- ^ . 6 Şubat 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Şubat 2018.
- ^ a b "BAKER, Prof. Alan". . 2019 (online bas.). A & C Black, an imprint of Bloomsbury Publishing plc. (üyelik veya Birleşik Krallık halk kütüphanesi üyeliği gereklidir) (abonelik gereklidir)
- ^ . 6 Ocak 2013 tarihinde kaynağından arşivlendi.
- ^ a b P. Turán, On the work of Alan Baker, Actes du Congrès International des Mathématiciens, Nice, 1970 Vol. 1 (Paris, 1971), ss. 3-5.
- ^ H. Halberstam, Review: Transcendental Number Theory, by Alan Baker, The Mathematical Gazette 59 (410) (1975), ss. 280-282.
- ^ D. Singmaster, Review: A Concise Introduction to the Theory of Numbers, by Alan Baker, The Mathematical Gazette 69 (450) (1985), 318-319.
- ^ A. Baker, Some historical remarks on number theory, Historia Mathematica 2 (1975), ss. 549-553.
- ^ Professor Alan Baker 4 Şubat 2021 tarihinde Wayback Machine sitesinde ., Department of Pure Mathematics and Mathematical Statistics, University of Cambridge (2014).
- ^ P. Turán, Alan Baker, in M. Atiyah and D. Iagolnitzer (eds.), Fields Medallists Lectures (World Sci. Publ., Singapore, 1997), s. 161.
- ^ Biography 4 Nisan 2008 tarihinde Wayback Machine sitesinde . in Encyclopædia Britannica.
- ^ "List of Fellows of the American Mathematical Society". 13 Ağustos 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Kasım 2012.
- ^ . 18 Şubat 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Haziran 2018.
- ^ Stolarsky, Kenneth B. (1978). "Review: Transcendental number theory by Alan Baker; Lectures on transcendental numbers by Kurt Mahler; Nombres transcendants by Michel Waldschmidt" (PDF). Bull. Amer. Math. Soc. 84 (8): 1370-1378. doi:10.1090/S0002-9904-1978-14584-4.[]
Kaynakça
- Alan Baker 6 Kasım 2018 tarihinde Wayback Machine sitesinde ., Heidelberg Laureate Forum.
- J. C. Peral, Alan Baker: transcendental work (İspanyolca), Gac. R. Soc. Mat. Esp. 4 (2) (2001), 437-445.
İlave okumalar
- B. Sury, (Temmuz 2018), Alan Baker (19 August 1939–04 February 2018) 4 Şubat 2021 tarihinde Wayback Machine sitesinde .
- ALAN BAKER 1 Kasım 2020 tarihinde Wayback Machine sitesinde . by David Masser.
- Masser, David (Ocak 2019). "Alan Baker 1939–2018" (PDF). . 66 (1): 32-35. 14 Şubat 2020 tarihinde kaynağından (PDF). Erişim tarihi: 30 Ocak 2021.
- Yann Bugeaud, (Temmuz 2018), On Some Results of Alan Baker
- Yuval Z. Flicker, Alan Baker, as I knew him[], Hardy-Ramanujan Journal 42(2019), ss. 12-16
- Gisbert Wüstholz, Remembrance of Alan Baker[], Hardy-Ramanujan Journal 42(2019), ss. 4-11
- David Masser, Alan Baker: My reminiscences 4 Şubat 2021 tarihinde Wayback Machine sitesinde ., Hardy-Ramanujan Journal 42(2019), ss. 1-3
Dış bağlantılar
- O'Connor, John J.; Robertson, Edmund F., "Alan Baker", MacTutor Matematik Tarihi arşivi
- Mathematics Genealogy Project'te Alan Baker
- O'Connor, John J.; Robertson, Edmund F., "Obituary: Guardian", MacTutor Matematik Tarihi arşivi veya . 3 Şubat 2021 tarihinde kaynağından arşivlendi.
- . 17 Eylül 2019 tarihinde kaynağından arşivlendi.
- . 23 Ağustos 2017 tarihinde kaynağından arşivlendi.
- . 5 Şubat 2021 tarihinde kaynağından arşivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Alan Baker FRS 19 Agustos 1939 4 Subat 2018 sayi teorisindeki etkili yontemler ozellikle de dogan konular uzerine yaptigi calismalarla taninan Ingiliz bir matematikciydi Alan BakerDogum19 Agustos 1939 1939 08 19 Londra IngiltereOlum04 Subat 2018 78 yasinda Cambridge IngiltereOlum sebebiserebrovaskuler hastalikMilliyetIngilizVatandaslikBirlesik KrallikEgitimUniversity College London Trinity College Cambridge UniversitesiMezun oldugu okul lar University of CambridgeTaninma nedeniOdullerFields Madalyasi 1970 1972 Fellow of the American Mathematical Society Fellow of the Royal SocietyKariyeriDaliMatematik Sayi teorisiCalistigi kurumUniversity of CambridgeTezSome Aspects of Diophantine Approximation 1964 Doktora danismaniDoktora ogrencileriHayati1950 lerde Alan Baker Alan Baker 19 Agustos 1939 da Londra da dogdu Dogu Londra daki a katildi ve akademik kariyeri kazandigi Eyalet Bursu ile University College London da un ogrencisi olarak basladi ve daha sonra Trinity College Cambridge de doktorasini Some Aspects of Diophantine Approximation Diophantine Yaklasimi nin Bazi Yonleri adli teziyle aldi 1961 de Matematikte Birinci Sinif Seref Odulu ne layik goruldu Aslinda doktora tezini sunmadan once sekiz makalesi basilmisti Askin sayilarin surekli kesirleri Continued fractions of transcendental numbers 1962 Mahler in askin sayilar siniflandirmasi uzerine On Mahler s classification of transcendental numbers 1964 Belirli cebirsel sayilara rasyonel yaklasimlar Rational approximations to certain algebraic numbers 1964 Littlewood un Diophantine yaklasim probleminin bir benzeri uzerine On an analogue of Littlewood s Diophantine approximation problem 1964 Belirli rasyonel sayilarin logaritmalarina yaklasimlar Approximations to the logarithms of certain rational numbers 1964 2 ve diger cebirsel sayilarin kup kokune rasyonel yaklasimlar Rational approximations to the cube root of 2 and other algebraic numbers 1964 Cebirsel fonksiyonlari temsil eden kuvvet serileri Power series representing algebraic functions 1965 ve Ustel islevi iceren bazi Diophantine esitsizlikleri uzerine On some Diophantine inequalities involving the exponential function 1965 1965 te Trinity College Uyesi secildi 1964 65 akademik yilini University College London Matematik Bolumu nde gecirdi Baker 1964 ten 1968 e kadar Cambridge de arastirma gorevlisiydi ardindan 1968 den 1974 e Saf Matematik Profesoru olarak atandigi 1974 e kadar surdurdugu Matematik Calismalari Direktoru oldu Cambridge deki kariyeri boyunca Amerika Birlesik Devletleri nde zaman gecirdi 1970 te Princeton daki Ileri Calismalar Enstitusu nun bir uyesi ve 1974 te Stanford da misafir profesor oldu Ayni zamanda 1988 de Hong Kong Universitesi nde 1989 da Eidgenossische Technische Hochschule Zurich te ve 1993 te Matematik Bilimleri Arastirma Enstitusu Berkeley California da misafir profesor oldu 31 yasinda 1970 yilinda Nice deki Uluslararasi Kongre de Fields Madalyasi ile odullendirildiginde de misafir arastirmaci olarak bulunuyordu Bu odulu Diophantine denklemleri uzerindeki calismasi icin aldi Bu tarihsel ortami ilk veren Paul Turan tarafindan asagidaki sekilde anlatilmistir tarafindan 1844 te baslatilan askin sayilar teorisi son yillarda buyuk olcude zenginlesti Ilgili derin katkilar arasinda Alan Baker Wolfgang M Schmidt ve Vladimir Gennadievich Sprindzuk un katkilari bulunmaktadir Calismalari bagimsiz degiskenin sifir olmayan tum cebirsel degerleri icin askin degerler varsayan onemli fonksiyon siniflarini bulma konusundaki geleneksel yogunlasma ile tezat olusturan onemli yonlere dogru ilerliyor Bunlarin arasinda matematikteki diger problemler uzerinde en agir etkiyi Baker in yaptigi gorulmustur Belki de bu etkilerden en onemlisi Diophantine denklemlerine yapilan uygulama olmustur Bin yildan daha uzun bir tarihe sahip olan bu teori bu yuzyilin ilk yillarina kadar ustaca gecici yontemlere tabi tutulmus izole problemlerin bir koleksiyonundan biraz daha fazlasiydi 1909 da f x y m displaystyle f x y m formundaki tum Diophantine denklemlerini ispatlayarak genel sonuclara atilim yapan kisi Axel Thue du burada m displaystyle m bir tamsayidir ve f displaystyle f en az uc derecenin indirgenemez homojen ikili bicimi olup tam sayi katsayilari ile tam sayilarda en fazla sonlu cok sayida cozume sahiptir Turan Carl Siegel ve Klaus Roth un bu sonuclarin tutacagi ve hatta cozum sayisini sinirlayacagi Diophantine denklem siniflarini genellestirdigini soylemeye devam ediyor Baker daha da ileri gitti ve en azindan prensipte bu tur problemlerin tam cozumune yol acabilecek sonuclar uretti Yukarida aciklanan f x y m displaystyle f x y m turundeki denklemler icin yalnizca m displaystyle m ye ve f displaystyle f nin tam sayi katsayilarina bagli olan bir B displaystyle B siniri oldugunu kanitladi max x0 y0 B displaystyle max x 0 y 0 leq B f x y m displaystyle f x y m nin herhangi bir x0 y0 displaystyle x 0 y 0 cozumu icin Elbette bu yalnizca sinirli sayida olasiligin dikkate alinmasi gerektigi anlamina gelir bu nedenle en azindan prensipte sonlu olasi cozumlerin her birini kontrol ederek cozumlerin tam listesi belirlenebilir 1974 te Cambridge Universitesi nde Saf Matematik Profesoru olarak atandi 2006 da olana kadar bu pozisyonda kaldi 1964 ten olumune kadar Trinity Koleji nin bir uyesiydi Turan Baker hakkindaki sozlerini asagidaki sekilde bitiriyor Baker in calismalarinin iki seyi cok ikna edici bir sekilde ornekledigini belirtiyorum Birincisi bir problemi cozmek icin bir teori baslatmaya layik egilimin yani sira belirli zor problemlere dogrudan saldirmak da ise yarar Ikinci olarak derin bir problemin dogrudan cozumunun kendisini oldukca dogal bir sekilde saglikli bir teori haline getirdigini ve matematigin onemli problemleriyle erken ve verimli bir temasa gectigini gosterir Baker in unlu kitaplari arasinda sunlar yer almaktadir Askin sayi teorisi Transcendental number theory 1975 Askinlik teorisi gelismeler ve uygulamalar Transcendence theory advances and applications 1977 Sayilar teorisine kisa bir giris A concise introduction to the theory of numbers 1984 Gisbert Wustholz ile birlikte Logaritmik formlar ve Diophantine geometrisi Logarithmic forms and Diophantine geometry 2007 ve Sayi Teorisinde Kapsamli Bir Ders A Comprehensive Course in Number Theory 2012 Transandantal sayi teorisine 1975 giriste Baker in asagidaki ifadesi yer almaktadir Askin sayilarin incelenmesi simdi matematigin yaygin dallarini zenginlestiren verimli ve kapsamli bir teori haline geldi Amacim bu alandaki son buyuk kesiflerin kapsamli bir hesabini saglamakti Anlatim sirasinda konunun klasik yonleri tartisilir Konudaki ispatlar uzun ve karmasik olma egilimindedir ve bu nedenle ayrintili islem icin yalnizca en temel sonuclari secmek gerekli olmustur dahasi genel olarak konusmak gerekirse bugune kadar bilinen en guclu onermelere yol acan veya en genis uygulamayi saglayan argumanlara vurgu yapilmistir Robert Tijdeman bu kitabin bir incelemesinde soyle yaziyor Yazar planinda basarili oldu Bu kitap askin sayi teorisinin onemli noktalarina ozellikle de yazarin 1970 yilinda Fields madalyasiyla odullendirildigi kendi onemli katkilarina dair bir inceleme sunar Askinlik teorisine genel bir bakis elde etmek isteyen matematikciler icin cok yararli bir yayindir teknikleri ve uygulanabilirligi Tarz son derece yogun ancak daha ayrintili calisma icin bircok referans var Sunum cok iyi yapilmis Bu kitap ayni zamanda Heini Halberstam 1926 2014 tarafindan da incelenmistir Yazar sadece 130 sayfalik bir alan icinde Adams Odulu makalesine dayanarak modern askinlik teorisinin panoramik bir aciklamasini veriyor Bunun artik matematigin genis dallarini zenginlestiren verimli ve kapsamli bir teori oldugu gercegi buyuk olcude katkilarindan dolayi 1970 yilinda Fields Madalyasi Nobel matematik Odulu ile odullendirilen yazarin kendisine baglidir Duz yazi net ve ekonomiktir ancak bir kisilik duygusu yansitan renk parlamalari ile serpistirilmistir ve her bolum sonraki konunun yararli bir ozetiyle baslar Tum asamalardaki matematiksel arguman oldukca yogunlastirilmistir cunku aslinda bu kadar cok zemini kapsayan kisa bir arastirma monografisinde kacinilmazdir Yeni baslayanlara daha merhametli davranmadigi icin yazari kinayabilir ancak yeni baslayan biri bile kitaptan bu son derece zor alanda bugune kadarki en buyuk basarilarin neler oldugu ve onemli sorunlarin neler oldugu konusunda net bir izlenim edinebilirken digerleri icin burada cok sayida verimli calisma grubu icin bol miktarda materyal bulunmaktadir Baker in 1984 tarihli Kisa Giris Concise Introduction yazisini inceleyen Don Redmond soyle yazar Pek cok kitap adlarina uymaz ancak bu kesinlikle adina uyan bir kitaptir Kitap cok ozlu ve standart bir dersin temel noktalarini kapsadigi icin guzel bir referans olabilir ancak elestirmen onu sayi teorisindeki ilk dersin tek ders kitabi olarak kullanabileceginden emin degildir Kisa Giris i de inceleyen David Singmaster soyle yaziyor Sayi teorisine giris konusundaki calismalar cok sayidadir bu nedenle herhangi bir yeni calisma yenilik acisindan incelenmelidir Bu kitap Cambridge Universitesi nde bir dersi icin ders materyaldir Sonuc olarak ozlu abarti degildir Genel olarak kitap bir yogunlasma harikasidir Bu 91 sayfalik metnin tamami ana materyale ayrilmis olsa bile dogru olacaktir ancak kendisi daha da yogunlastirmis ve ek materyali icin yaklasik 30 sayfa kullanmistir Bu gordugum mevcut sayi teorisinin en kullanisli ozetini icerir Yetkili bir indeks var boylece sonuclarin yeri belirlenebilir Bu kitabi alanla ilgili bir arastirma yapmak isteyen herhangi ciddi bir lisans ogrencisine tavsiye ederim ancak kanitlarin cok dikkatli olmasi gerektigi konusunda onu uyaririm Sayi teorisinde bir gecmisi olan herkes Baker in mevcut bilgi aciklamasini cok begenecektir Yuri Bilu Baker ve Wustholz un 2007 tarihli Logaritmik formlar ve Diofantin geometrisi kitabinin bir incelemesinde sunlari ifade etmektedir Uzun zamandir beklenen bu kitap Baker Masser ve Wustholz un hem lisans hem de lisansustu ogrencilerine uygun bir bicimde klasik calismalarina giris niteligindedir Bu kitap gercekten bir giris niteligindedir Amaci teknik ozelliklerden kacinirken ilkeleri ogretmektir Bu icerige belirli sinirlamalar getirir Yazarlar carpimsal grup icin nitel teoriyi cok ayrintili olarak ele alirlar ancak nicel acidan fazla bir sey soylemezler ve sadece kisaca degismeli cesitlerden soz ederler Bununla birlikte bu kitap Baker Masser Wustholz ve digerlerinin yukarida siralanan konularda orijinal dergi makalelerini incelemek icin gerekli sezgisel arka plani saglar Baker ayrica askinlik teorisindeki 1988 onemli Yeni gelismeleri duzenledi ve Gisbert Wustholz ile onumuzdeki bin yilda Sayi teorisi askinlik ve Diophantine geometrisi baslikli onemli calismayi yazdi Bu askinlik teorisi ve ilgili matematikteki basarilarin ve acik problemlerin bir arastirmasidir 1999 da Baker in 60 dogum gununu kutlamak icin Zurih te bir konferans duzenlendi Toplantilarda verilen derslerin cogu A Panorama in Number Theory or The View from Baker s Garden 2002 adli eserde yayinlandi Kitaba giris su sekilde basliyor Alan Baker in 60 dogum gunu ile birlikte milenyum sayi teorisinde bir toplanti duzenlemek ve bu alandaki onde gelen uluslararasi arastirmacilardan olusan bir grubu bir araya getirmek icin tekil bir firsat sundu Forschungsinstitut fur Mathematik ile birlikte ETH Zurich tarafindan comertce desteklendi Bu bizi buyuk bir sayi teorisi yelpazesini ve ilgili geometriyi ozellikle Diophantine yonlerine vurgu yaparak kapsamayi amaclayan bir program gelistirmeye tesvik etti Londra Matematik Dernegi Baskani Profesor Martin Taylor tarafindan temsil edildi ve 60 dogum gunu vesilesiyle Alan Baker a selamlar gonderdi Baker sayi teorisinin tarihi ozellikle de askin sayilar uzerine aciklamalar yapar Peki bu bize matematigin tarihsel evrimi hakkinda ne soyluyor Birincisi Profesor Dieudonne nin terminolojisinde birkac anahtar sorunun cekim merkezlerinin cok onemli bir rol oynadigi aciktir Bu sayi teorisi icin diger matematigin dallarindan daha dogru olabilir ancak tum iyi calismalarin bir dereceye kadar bu tur merkezler tarafindan yonlendirildigine inaniyorum Tartismakta oldugum belirli alanin genel egilimini ozetlemek zordur cunku gelisiminde pek cok yeni kivrimlar ve donusler yer almistir ancak evrimdeki acik bir unsur sayi teorisi ve cebirden gelen fikirlerin klasik fonksiyon teorisinin giderek daha genis kullanimiyla basarili bir sekilde harmanlanmasi veya birlestirilmesidir Ve inaniyorum ki aktif bir teorinin yaratilmasinda temel bileseni olusturan cesitli kavramlarin bu yakinsamasidir Profesor Dieudonne ye gore askin sayilarin incelenmesi sadece bir yontem olma yolundadir Bununla birlikte cozmede araci oldugu problemlerin cesitli dogasi goz onune alindiginda son asamaya birkac yil once ulastigina dair cok az suphe var gibi gorunuyor ve aslinda bu halihazirda Profesor Dieudonne nin dilinde bir cekim merkezi olma yolunda oldugu ortaya cikiyor Baker in Cambridge Universitesi sayfasinda verilen arastirma ilgi alanlari Ocak 2014 te derlenmistir Cebirsel sayilarin logaritmalarinin dogrusal bagimsizligina dair Baker Teoremi son otuz yilda sayi teorisindeki cok cesitli gelismelerin anahtari olmustur Bunlarin en onemlileri Diofantin denklemlerinin etkili cozumune sinif numarasi problemlerinin cozumune p sel L fonksiyonlari teorisine ve ozellikle Masser ve Wustholz un calismalari araciligiyla aritmetik cebirsel geometrinin bircok derin yonune yapilan uygulamalardir Teori gunumuze kadar cok verimli arastirma kaynagi olmaya devam ediyor Ayrica genel ilgi alanlari sayi teorisi ve Diophantine analiziydi Baker matematigin disinda ilgi alanlarini seyahat fotograf ve tiyatro olarak siraliyor BasarilariBaker ayrica a ve q cebirsel oldugunda qa displaystyle q a nin askin veya askin olmadigi sorulan onemli katkilarda bulundu Hilbert in kendisi bu problemin Riemann varsayiminin cozumunden daha zor olmasini bekledigini belirtti Ancak 1934 te Aleksandr Gelfond ve Theodor Schneider tarafindan bagimsiz olarak cozuldu ancak Baker genis bir genellemesini elde etmeyi basardi Bu calismadan daha once tanimlanmamis buyuk bir askin sayilar kategorisi olusturdu ve temeldeki teorinin cok cesitli Diophantine problemlerini cozmek icin nasil kullanilabilecegini gosterdi Baker ozellikle sunu gosterdi a1 an displaystyle alpha 1 alpha n cebirsel sayilardir 0 veya 1 disinda ve eger b1 bn displaystyle beta 1 beta n 1 b1 bn displaystyle 1 beta 1 beta n rasyonel sayilardan dogrusal olarak bagimsiz olan irrasyonel cebirsel sayilarsa bu durumda a1b1a2b2 anbn displaystyle alpha 1 beta 1 alpha 2 beta 2 cdots alpha n beta n sayisi askindir Baker 1970 Fields madalyasina ek olarak matematiksel katkilarindan dolayi bircok onursal odul aldi Bunlar arasinda Cambridge Universitesi nden Adams odulu 1972 ve Royal Society of London secimi 1973 yer aliyor Universite Louis Pasteur Strasbourg dan 1998 fahri doktora unvani aldi University College London da 1979 fahri bursiyeri Hindistan Bilim Akademisi 1980 Hindistan Ulusal Bilimler Akademisi nin yabanci bursiyeri 1993 Academia Europaea nin 1998 bir uyesi ve Macar Bilimler Akademisi nin 2001 onursal uyesidir 2012 de American Mathematical Society nin bir uyesi oldu Ayrica yabanci bir uyesi oldu Bazi yayinlariBaker Alan 1966 Linear forms in the logarithms of algebraic numbers I 13 2 ss 204 216 doi 10 1112 S0025579300003971 ISSN 0025 5793 MR 0220680 Baker Alan 1967a Linear forms in the logarithms of algebraic numbers II cilt 14 ss 102 107 doi 10 1112 S0025579300008068 ISSN 0025 5793 MR 0220680 Baker Alan 1967b Linear forms in the logarithms of algebraic numbers III 14 2 ss 220 228 doi 10 1112 S0025579300003843 ISSN 0025 5793 MR 0220680 Baker Alan 1990 Transcendental number theory Cambridge Mathematical Library 2 bas Cambridge University Press ISBN 978 0 521 39791 9 MR 0422171 1st edition 1975 Baker Alan Wustholz G 2007 Logarithmic forms and Diophantine geometry New Mathematical Monographs 9 Cambridge University Press ISBN 978 0 521 88268 2 MR 2382891 Baker Alan A Concise Introduction to The Theory of Numbers PDF Cambridge University Press ISBN 0 521 28654 9 31 Mart 2020 tarihinde kaynagindan PDF Erisim tarihi 30 Ocak 2021 Onurlandirilmasi ve odulleri1970 Fields Madalyasi 1972 1973 Kraliyet Cemiyeti BursuNotlar 6 Subat 2018 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Subat 2018 a b BAKER Prof Alan 2019 online bas A amp C Black an imprint of Bloomsbury Publishing plc uyelik veya Birlesik Krallik halk kutuphanesi uyeligi gereklidir abonelik gereklidir 6 Ocak 2013 tarihinde kaynagindan arsivlendi a b P Turan On the work of Alan Baker Actes du Congres International des Mathematiciens Nice 1970 Vol 1 Paris 1971 ss 3 5 H Halberstam Review Transcendental Number Theory by Alan Baker The Mathematical Gazette 59 410 1975 ss 280 282 D Singmaster Review A Concise Introduction to the Theory of Numbers by Alan Baker The Mathematical Gazette 69 450 1985 318 319 A Baker Some historical remarks on number theory Historia Mathematica 2 1975 ss 549 553 Professor Alan Baker 4 Subat 2021 tarihinde Wayback Machine sitesinde Department of Pure Mathematics and Mathematical Statistics University of Cambridge 2014 P Turan Alan Baker in M Atiyah and D Iagolnitzer eds Fields Medallists Lectures World Sci Publ Singapore 1997 s 161 Biography 4 Nisan 2008 tarihinde Wayback Machine sitesinde in Encyclopaedia Britannica List of Fellows of the American Mathematical Society 13 Agustos 2013 tarihinde kaynagindan arsivlendi Erisim tarihi 3 Kasim 2012 18 Subat 2017 tarihinde kaynagindan arsivlendi Erisim tarihi 2 Haziran 2018 Stolarsky Kenneth B 1978 Review Transcendental number theory by Alan Baker Lectures on transcendental numbers by Kurt Mahler Nombres transcendants by Michel Waldschmidt PDF Bull Amer Math Soc 84 8 1370 1378 doi 10 1090 S0002 9904 1978 14584 4 olu kirik baglanti KaynakcaAlan Baker 6 Kasim 2018 tarihinde Wayback Machine sitesinde Heidelberg Laureate Forum J C Peral Alan Baker transcendental work Ispanyolca Gac R Soc Mat Esp 4 2 2001 437 445 Ilave okumalarB Sury Temmuz 2018 Alan Baker 19 August 1939 04 February 2018 4 Subat 2021 tarihinde Wayback Machine sitesinde ALAN BAKER 1 Kasim 2020 tarihinde Wayback Machine sitesinde by David Masser Masser David Ocak 2019 Alan Baker 1939 2018 PDF 66 1 32 35 14 Subat 2020 tarihinde kaynagindan PDF Erisim tarihi 30 Ocak 2021 Yann Bugeaud Temmuz 2018 On Some Results of Alan Baker Yuval Z Flicker Alan Baker as I knew him olu kirik baglanti Hardy Ramanujan Journal 42 2019 ss 12 16 Gisbert Wustholz Remembrance of Alan Baker olu kirik baglanti Hardy Ramanujan Journal 42 2019 ss 4 11 David Masser Alan Baker My reminiscences 4 Subat 2021 tarihinde Wayback Machine sitesinde Hardy Ramanujan Journal 42 2019 ss 1 3Dis baglantilarO Connor John J Robertson Edmund F Alan Baker MacTutor Matematik Tarihi arsivi Mathematics Genealogy Project te Alan Baker O Connor John J Robertson Edmund F Obituary Guardian MacTutor Matematik Tarihi arsivi veya 3 Subat 2021 tarihinde kaynagindan arsivlendi 17 Eylul 2019 tarihinde kaynagindan arsivlendi 23 Agustos 2017 tarihinde kaynagindan arsivlendi 5 Subat 2021 tarihinde kaynagindan arsivlendi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

