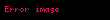Olasılık kuramı içinde bir olasılık dağılımı eğer bir olasılık kütle fonksiyonu ile karakterize edilmiş ise ayrık olarak anılır. Böylelikle bir rassal değişken olan X için dağılım ayrık ise o zaman X bir ayrık rassal değişken olarak bilinir. Bu halde


olur ve burada u X için bütün mümkün değerler serisini ihtiva eder. Böyle bir rassal değişken ancak sayılı veya sayılabilir sonsuz sayılı değerler alabildiği bu tanımdan ortaya çıkar. Eğer mümkün değerler sayılabilir sonsuz tane ise ve her birinin olasılık değerinin toplamları 1'e eşit olmasi gerekmekte olması bu olasılık sayılarının pek hızlı bir şekilde 0'a erişmesini gerektirmektedir. Örneğin eğer
her n = 1, 2, ..., için ise
olasılıkların toplamı şudur:
1/2 + 1/4 + 1/8 + ... = 1.
Klasik tanım
Olasılık kuramı geliştirilmesinin ilk safhalarında olasılık şans aletleri ile açıklanmakta idi. Şu şans aletleri sayılabilir: havaya atılan bir madeni paranın yazı-tura gelmesi, altı yüzlü bir zar atılması, üstü sektörel parçalara bölünmüş bir döner alet (örneğin rulet tekerleği), iskambil kâğıtları, içinde belirli sayıda değişik nesne bulunan küp veya küp benzerleri. Bu halde belirtilmiş bir olay ortaya çıkması için olasılık, her mümkün sonucu eşit olasılıklı olan örneklem uzayında incelenmektedir. Bunlardan benzerlik çıkarılarak, olasılık incelenen olaya uygun sonuç sayısının toplam tüm sonuçlar sayısına oranı olarak tanımlanmıştı. Örneğin, incelenecek sorun "tek bir zar atılınca çift sayıların gelme olasılığı nedir" şeklinde olsun. Zar yansız olup her altı yüzü de eşit olasılıkla gelebileceği için, 2, 4, 6 sonuçları 3 tane olduğu ve toplam mümkün sonuç sayısı 6 yüze dayanarak 6 olduğu için, aranan olasılık
- P( 2 veya 4 veya 6 ) =
olarak bulunur.
Modern tanım
Modern tanıma örneklem uzayı adı verilen bir küme ile başlanır; bu klasik tanımda kullanılan mümkün tüm sonuçlar seti ile aynı anlamlıdır; ve şu notasyon kullanılarak ifade edilir: 
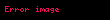

Bu demektir ki olasılık fonksiyonu olan f(x) Ω örneklem uzayında bulunan her x değeri için 0 ile 1 arasında bulunmaktadır ve x için tüm mümkün değerler için f(x) değerlerinin toplamı tama tam 1e eşit olur. Bir olay 
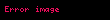
Buna göre tüm örneklem uzayının olasılığı 1e eşittir ve boş örneklem uzayı veya 0 olay için de olasılık 0a eşit olur.
Örneklem uzayındaki bir noktayı "olasılık" değerine eşleyen fonksiyona, yani 
olur.
Eğer bir rassal değişken aralıklı ise, sıfır-olmayan olasılık taşıyan her değerin seti, bir veya olan, sayıda bir settir. Bu mümkün değerler seti topolojik olarak ayrık bir settir çünkü set içindeki her nokta tek tekdir; diğerlerinden ayrılmıştır ve bu noktalar sayılabilir.
Ayrık dağılımlar arasında en iyi bilinenleri Poisson dağılımı, Bernoulli dağılımı, binom dağılım, geometrik dağılım, negatif binom dağılımıdir.
Değişik bir tanımlama
Yukarıda verilen tanıma benzer olarak, fakat değişik bir bakışla, bir ayrık rassal değişken için yığmalı dağılım fonksiyonu yalnızca göstererek büyüme gösterir. Bu demektir ki yığmalı dağılım fonksiyonu daha büyük değere sıçrama yaptığı zaman büyüme gösterir ve bu sıçramayı yapmadan sabit kalır. Sıçrama yapılan noktalar aynen rassal değişkenin değer aldığı noktalardır. Bu türlü sıçramalar ya sonludur veya olurlar. Bu sıçrama noktalarının konumu topolojik olarak ayrık olmayabilir; örneğin yığmalı olasılık dağılımı her rasyonel sayıda sıçrama gösterebilir.
Gösterge fonksiyonları terimleri ile ifade edilme
Bir ayrık rassal değişken X için u0, u1, ... sıfır olmayan olasılık değerler aldığı varsayılan sayılar olsun. Şu fonksiyon gösterilsin
Bunlar ve formül (1) nedeniyle
Bundan çıkarılır ki Xin u0, u1, ... dışında alabileceği herhangi bir değer için olasılık 0 olur. O halde, sıfır olasılıklı değerler setinin dışında X şöyle yazılabilir:
Burada 

Örnekler
Örnek olarak şu önemli ayrık olasılık dağılımlar verilmektedir. Bu liste mümkün olan tüm ayrık olasılık dağılımları ihtiva etmemektedir:
- Ayrık tekdüze dağılım: Bir sonlu set içinde bulunan tüm elemanlar aynı eşit olabilirliktedirler. Bu teorik olarak bir hilesiz madeni para, bir kusursuz zar, bir kumarhane rulet tekerleği veya iyice karılmış iskambil kâğıtları için uygun olan olasılık dağılımıdır. Bilgisayarların yaygın olarak kullanılması sonucu özel veya genel işlerde kullanılan bilgisayarlar olarak kullanılıp ayrık tekdüze rassal değişken sayıları üretilmektedir.
- Bernoulli dağılımı: 1 değeri için p olasılığı ve 0 değeri için q = 1 - p olasılığı alır.
- Binom dağılım: Bir seri bağımsız Evet/Hayır (Başarılı/Başarısız) sonuçlu deneylerdeki başarılılık sayısını tanımlar.
- Poisson dağılımı: Belli bir zaman aralığında (veya belirli bir birim aralık içinde) teker teker, az olabilirlikli olarak ortaya çıkan çok büyük sayıda olayları tanımlar.
- Geometrik dağılım: Bir seri Evet/Hayır sonuçlu denemelerde birinci başarıyı elde etmek için gerekli deneme sayısının olasılığını açıklar.
- Hipergeometrik dağılım: Eğer toplam başarılılık sayısı bilinirse, n tane bağımsız Evet/Hayır (Başarılı/Başarısız) deneylerde ilk m sayıda başarılılık olasılığını tanımlar.
- Bozulmuş dağılım: Sadece x0da bulunur. Burada X mutlaka hiç olasılıksız x0 değeri alır. Bu rassal gibi gözükmez ama matematikte verilen rassal değişken tanımlamasına uygunluk gösterir. Bu dağılım belirli deterministik değişkenler ile rassal değişkenlerinin ayni matematiksel biçimde incelenmesine imkân verir.
Ayrıca bakınız
Dış bağlantılar
- Yeni öğrenenler İçin olasılık dağılımları. 3 Aralık 2013 tarihinde Wayback Machine sitesinde . (İngilizce)
- Bilgisayarda etkileşimli aralıklı ve sürekli olasılık dağılımları 22 Şubat 2008 tarihinde Wayback Machine sitesinde . (İngilizce)
- Çok kullanılan olasılık dağılımları için ayrıntılı özetler 3 Temmuz 2008 tarihinde Wayback Machine sitesinde . (İngilizce)
- Olasılık dağılımları - Genel görüş 5 Mart 2008 tarihinde Wayback Machine sitesinde . (İngilizce)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik kurami icinde bir olasilik dagilimi eger bir olasilik kutle fonksiyonu ile karakterize edilmis ise ayrik olarak anilir Boylelikle bir rassal degisken olan X icin dagilim ayrik ise o zaman X bir ayrik rassal degisken olarak bilinir Bu haldeBir ayrik olasilik dagilimi icin olasilik kutle fonksiyonu Tek veri degerleri olan 1 3 ve 7 icin olasilik degerleri 0 2 0 5 0 3 olarak bulunur Bu degerleri kapsamayan bir veri seti icin olasilik sifir olur Yukaridan asagiya dogru bir ayrik olasilik dagilimi icin bir surekli olasilik dagilimi icin ve hem surekli hem de ayrik kisimlari bulunan bir olasilik dagilimi icin yigmali olasilik fonksiyonu uPr X u 1 displaystyle sum u Pr X u 1 olur ve burada u X icin butun mumkun degerler serisini ihtiva eder Boyle bir rassal degisken ancak sayili veya sayilabilir sonsuz sayili degerler alabildigi bu tanimdan ortaya cikar Eger mumkun degerler sayilabilir sonsuz tane ise ve her birinin olasilik degerinin toplamlari 1 e esit olmasi gerekmekte olmasi bu olasilik sayilarinin pek hizli bir sekilde 0 a erismesini gerektirmektedir Ornegin eger her n 1 2 icin Pr X n 12n displaystyle Pr X n tfrac 1 2 n ise olasiliklarin toplami sudur 1 2 1 4 1 8 1 Klasik tanimOlasilik kurami gelistirilmesinin ilk safhalarinda olasilik sans aletleri ile aciklanmakta idi Su sans aletleri sayilabilir havaya atilan bir madeni paranin yazi tura gelmesi alti yuzlu bir zar atilmasi ustu sektorel parcalara bolunmus bir doner alet ornegin rulet tekerlegi iskambil kagitlari icinde belirli sayida degisik nesne bulunan kup veya kup benzerleri Bu halde belirtilmis bir olay ortaya cikmasi icin olasilik her mumkun sonucu esit olasilikli olan orneklem uzayinda incelenmektedir Bunlardan benzerlik cikarilarak olasilik incelenen olaya uygun sonuc sayisinin toplam tum sonuclar sayisina orani olarak tanimlanmisti Ornegin incelenecek sorun tek bir zar atilinca cift sayilarin gelme olasiligi nedir seklinde olsun Zar yansiz olup her alti yuzu de esit olasilikla gelebilecegi icin 2 4 6 sonuclari 3 tane oldugu ve toplam mumkun sonuc sayisi 6 yuze dayanarak 6 oldugu icin aranan olasilik P 2 veya 4 veya 6 36 12 displaystyle tfrac 3 6 tfrac 1 2 olarak bulunur Modern tanimModern tanima orneklem uzayi adi verilen bir kume ile baslanir bu klasik tanimda kullanilan mumkun tum sonuclar seti ile ayni anlamlidir ve su notasyon kullanilarak ifade edilir W x1 x2 displaystyle Omega left x 1 x 2 dots right Sonra x W displaystyle x in Omega icinde bulunan her bir olasilik degeri f x displaystyle f x bagli oldugu varsayilir ve bu olasilik degerinin su ozellikleri bulundugu kabul edilir f x 0 1 butun x W displaystyle f x in 0 1 mbox butun x in Omega x Wf x 1 displaystyle sum x in Omega f x 1 Bu demektir ki olasilik fonksiyonu olan f x W orneklem uzayinda bulunan her x degeri icin 0 ile 1 arasinda bulunmaktadir ve x icin tum mumkun degerler icin f x degerlerinin toplami tama tam 1e esit olur Bir olay W displaystyle Omega orneklem uzayinin herhangi bir E displaystyle E altseti olarak tanimlanir E displaystyle E olayinin olasilik degeri ise soyle tanimlanir P E x Ef x displaystyle P E sum x in E f x Buna gore tum orneklem uzayinin olasiligi 1e esittir ve bos orneklem uzayi veya 0 olay icin de olasilik 0a esit olur Orneklem uzayindaki bir noktayi olasilik degerine esleyen fonksiyona yani f x displaystyle f x fonksiyonuna olasilik kutle fonksiyonu adi verilir Bir olasilik dagilimi eger bir olasilik kutle fonksiyonu ile karakterize edilmis ise ayrik dagilim olarak nitelendirilir Bir X rassal degiskeni icin dagilim ayrik ise o halde X bir ayrik rassal degisken olarak tanimlanir ve Xin butun mumkun degerler serisini ihtiva eden u icin uPr X u 1 displaystyle sum u Pr X u 1 olur Eger bir rassal degisken aralikli ise sifir olmayan olasilik tasiyan her degerin seti bir veya olan sayida bir settir Bu mumkun degerler seti topolojik olarak ayrik bir settir cunku set icindeki her nokta tek tekdir digerlerinden ayrilmistir ve bu noktalar sayilabilir Ayrik dagilimlar arasinda en iyi bilinenleri Poisson dagilimi Bernoulli dagilimi binom dagilim geometrik dagilim negatif binom dagilimidir Degisik bir tanimlamaYukarida verilen tanima benzer olarak fakat degisik bir bakisla bir ayrik rassal degisken icin yigmali dagilim fonksiyonu yalnizca gostererek buyume gosterir Bu demektir ki yigmali dagilim fonksiyonu daha buyuk degere sicrama yaptigi zaman buyume gosterir ve bu sicramayi yapmadan sabit kalir Sicrama yapilan noktalar aynen rassal degiskenin deger aldigi noktalardir Bu turlu sicramalar ya sonludur veya olurlar Bu sicrama noktalarinin konumu topolojik olarak ayrik olmayabilir ornegin yigmali olasilik dagilimi her rasyonel sayida sicrama gosterebilir Gosterge fonksiyonlari terimleri ile ifade edilmeBir ayrik rassal degisken X icin u0 u1 sifir olmayan olasilik degerler aldigi varsayilan sayilar olsun Su fonksiyon gosterilsin Wi w X w ui i 0 1 2 displaystyle Omega i omega X omega u i i 0 1 2 dots Bunlar ve formul 1 nedeniyle Pr iWi iPr Wi iPr X ui 1 displaystyle Pr left bigcup i Omega i right sum i Pr Omega i sum i Pr X u i 1 Bundan cikarilir ki Xin u0 u1 disinda alabilecegi herhangi bir deger icin olasilik 0 olur O halde sifir olasilikli degerler setinin disinda X soyle yazilabilir X iai1Wi displaystyle X sum i alpha i 1 Omega i Burada ai Pr X ui displaystyle alpha i Pr X u i ve 1A displaystyle 1 A A icin bir Bu sonuc da ayrik rassal degiskenleri tanimlama icin bir alternatif olarak kullanilabilir OrneklerOrnek olarak su onemli ayrik olasilik dagilimlar verilmektedir Bu liste mumkun olan tum ayrik olasilik dagilimlari ihtiva etmemektedir Ayrik tekduze dagilim Bir sonlu set icinde bulunan tum elemanlar ayni esit olabilirliktedirler Bu teorik olarak bir hilesiz madeni para bir kusursuz zar bir kumarhane rulet tekerlegi veya iyice karilmis iskambil kagitlari icin uygun olan olasilik dagilimidir Bilgisayarlarin yaygin olarak kullanilmasi sonucu ozel veya genel islerde kullanilan bilgisayarlar olarak kullanilip ayrik tekduze rassal degisken sayilari uretilmektedir Bernoulli dagilimi 1 degeri icin p olasiligi ve 0 degeri icin q 1 p olasiligi alir Binom dagilim Bir seri bagimsiz Evet Hayir Basarili Basarisiz sonuclu deneylerdeki basarililik sayisini tanimlar Poisson dagilimi Belli bir zaman araliginda veya belirli bir birim aralik icinde teker teker az olabilirlikli olarak ortaya cikan cok buyuk sayida olaylari tanimlar Geometrik dagilim Bir seri Evet Hayir sonuclu denemelerde birinci basariyi elde etmek icin gerekli deneme sayisinin olasiligini aciklar Hipergeometrik dagilim Eger toplam basarililik sayisi bilinirse n tane bagimsiz Evet Hayir Basarili Basarisiz deneylerde ilk m sayida basarililik olasiligini tanimlar Bozulmus dagilim Sadece x0da bulunur Burada X mutlaka hic olasiliksiz x0 degeri alir Bu rassal gibi gozukmez ama matematikte verilen rassal degisken tanimlamasina uygunluk gosterir Bu dagilim belirli deterministik degiskenler ile rassal degiskenlerinin ayni matematiksel bicimde incelenmesine imkan verir Ayrica bakinizOlasilik dagilimiDis baglantilarYeni ogrenenler Icin olasilik dagilimlari 3 Aralik 2013 tarihinde Wayback Machine sitesinde Ingilizce Bilgisayarda etkilesimli aralikli ve surekli olasilik dagilimlari 22 Subat 2008 tarihinde Wayback Machine sitesinde Ingilizce Cok kullanilan olasilik dagilimlari icin ayrintili ozetler 3 Temmuz 2008 tarihinde Wayback Machine sitesinde Ingilizce Olasilik dagilimlari Genel gorus 5 Mart 2008 tarihinde Wayback Machine sitesinde Ingilizce
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans