Olasılık kuramında ve istatistikte, hipergeometrik dağılım sonlu bir içinden tekrar geri koymadan birbiri arkasına n tane nesnenin çekilmesi işlemi için başarı sayısının dağılımını bir ayrık olasılık dağılımı şekilde betimler.
| Olasılık kütle fonksiyonu | |
| Yığmalı dağılım fonksiyonu | |
| Parametreler | |
|---|---|
| Olasılık kütle fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | |
| Mod | |
| Varyans | |
| Çarpıklık | |
| Fazladan basıklık |
|
| Entropi | |
| Moment üreten fonksiyon (mf) | |
| Karakteristik fonksiyon | |
Yaygın bir örnek, hatalı ve hatasız malları sınıflandıran bir ihtimal tablosunda gösterilebilir:
| Çekilmiş | Çekilmemiş | Toplam | |
|---|---|---|---|
| Hatalı | k | m − k | m |
| Hatasız | n − k | N + k − n − m | N − m |
| Toplam | n | N − n | N |
İçinde m sayıdan daha fazla hatalı mal birimi olmadığını kabul ettiğimiz N birimlik bir mal teslimi yapılmıştır. Bu N sayıdaki malların içinden tam n sayıda bir örnek alınıp bunlar kontrolden geçilirse bu örnek içinde tam k tane hatalı mal birimi bulunacağı hipergeometrik dağılım ile açıklanır.
Genel olarak: Eğer bir X rassal değişkeni N, m ve n parametreleri olan bir hipergeometrik dağılım gösterirse, tam olarak k sayıda başarı elde edilmesi, şu fonksiyonla bulunur:
k değeri max(0, n+m−N) ile min(m, n) arasındaysa olasılık pozitiftir.
Bu formül şöyle daha da açıklanabilir: (Geri koyulmadan) alınabilmesi mümkün örnek sayısı 'dir. Hatalı nesne sayısının k olması için sayıda ihtimal bulunur; geride kalan kısmın hatasız nesnelerle doldurulması için de ihtimal mevcuttur.
k, 0 ve N arasında her tam sayı değeri alabildiği için ve olasılık değerlerinin toplamı 1 olduğu için, kombinatorik matematikte bu .
Uygulama ve bir örnek
Hipergeometrik dağılımın klasik uygulaması geri koymadan örnekleme adı verilebilen bir denemedir. Bir küp problemi düşünülsün: bir küpün içinde iki tip küçük top, beyaz ve siyah, bulunduğu düşünülsün. Aynen bir binom dağılımı için yapılan deneme gibi, küpten bir beyaz top çekmeye başarı adı verilsin ve alternatif olan siyah top çekmek başarısızlık sayılsın. N küpte bulunan toplam top sayısı, m küpteki beyaz top sayısı ve böylece N − m ise küpteki siyah top sayısı olsun. Şimdi küpün içinde 5 beyaz ve 45 siyah top olduğu varsayılsın. Gözleri kapalı olarak küpten birer birer 10 tane top çekilsin ve her çekilen top küpe geri konulmasın. Bu deneme geri koyulmadan örnekleme olur.
Araştırmayı ilgilendiren soru: Bu çekişte küpten tam 4 tane beyaz top çekme (yani ima ile 6 tane de siyah top çekme) olasılığı nedir? Buna binom dağılım modeli uygulanamaz; çünkü her çekilişte başarı olasılığı değişmektedir. Bu problem iki kategorik değişkeni sınıflandıran olumsallık tablosunda şöyle özetlenebilir:
| Çekilmiş | Çekilmemiş | Toplam | |
|---|---|---|---|
| Beyaz toplar | 4 (k) | 1 = 5 − 4 (m − k) | 5 (m) |
| Siyah toplar | 6 = 10 − 4 (n − k) | 39 = 50 + 4 − 10 − 5 (N + k − n − m) | 45 (N − m) |
| Toplam | 10 (n) | 40 (N − n) | 50 (N) |
Küpten tam olarak k tane beyaz top çekmenin olasılığı şu formül kullanılarak hesaplanir:
Bu problem için k = 4 olduğundan 4 tane beyaz top (ve 6 tane siyah top) çekme olasılığı
çok düşük bir değerde (yaklaşık 0,004) olup, olabilirliği nerede ise sıfıra eşittir. Bu bir değişik ifade ile açıklanırsa bu rassal deneme (yani içinde 50 top bulunan bir küpten 10 tane top çekip hiçbirini geri koyulmamasi denemesini) 1000 defa tekrarlanırsa 4 beyaz (ve 7 siyah) top elde etmek ancak 4 defa ortaya çıkan bir sonuç olacaktır.
Bu sefer küpten 5 tane beyaz (ve 5 tane siyah) top çekme olasılığına göz atılsın. İki kategorik değişkeni sınıflandıran olumsallık tablosu şöyle kurulur:
| Çekilmiş | Çekilmemiş | Toplam | |
|---|---|---|---|
| Beyaz toplar | 5 (k) | 0 = 5 − 5 (m − k) | 5 (m) |
| Siyah toplar | 5 = 10 − 5 (n − k) | 40 = 50 + 5 − 10 − 5 (N + k − n − D) | 45 (N − m) |
| Toplam | 10 (n) | 40 (N − n) | 50 (N) |
Olasılık şöyle hesaplanabilir (Dikkat edilirse paydalar hep aynıdır):
Beklendiği gibi 5 beyaz top çekme olasılığı, 4 beyaz top çekme olasılığının çok daha altındadır.
Simetriler
Hipergeometrik dağılımda n ve m parametreleri arasında çok önemli simetriler vardır. Bu simetriler verilen küp problemi için önemli değil gibi görünmektedirler. Gerçekten verilen bazı hipergeometrik dağılım gösteren problemlerde n ve m parametreleri hiçbir problem olmadan birbiriyle değiştirilebilir. Ancak hayat/ölüm sorunlarına hipergeometrik dağılım uygulanmaya başlayınca önemleri anlaşılabilir.
Parametreler olan n ve m arasındaki simetriler şöyle sıralanabilirler:
- Bu halde siyah ve beyaz en basitçe rol değiştirmektedirler.
- f(k;N,m,n) = f(n − k;N,N − m,n)
Bunu daha kolay anlamak için siyah toplar beyaza; beyaz toplar siyaha boyanınca neyin değiştiğini düşünmek gerektir.
- Bu halde çekilmiş ve çekilmemiş toplar rol değiştirmektedirler.
- f(k;N,m,n) = f(m − k;N,m,N − n)
- Bu simetriyi anlamak için topları çekme hareketini unutup, zaten çekilmiş olan toplara dikkat
çekilmektedir ve zaten çekilmiş olan toplara etiket yapıştırma işlemine benzer:
- f(k;N,m,n) = f(k;N,n,m)
İlişkili dağılımlar
X ~ Hypergeometrik(



- Eğer
ise
rassal değişkeni
parametreli bir Bernoulli dağılımı gösterir.
- Eğer 0 veya 1 e eşit olmayan
ve
ile karşılaştırılınca
ve
büyük değerlerde iseler, o halde
Burada 


- Eğer 0 veya 1 e eşit olmayan
ve
ile karşılaştırılınca
ve
büyük değerlerde iseler, o halde
Burada 
Ayrıca bakınız
Kaynakça
- Yazılım (C++ ve Ruby) kaynakları ile hipergeometrik dağılım hesaplayıcısı24 Şubat 2008 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik kuraminda ve istatistikte hipergeometrik dagilim sonlu bir icinden tekrar geri koymadan birbiri arkasina n tane nesnenin cekilmesi islemi icin basari sayisinin dagilimini bir ayrik olasilik dagilimi sekilde betimler Hipergeometrik Olasilik kutle fonksiyonuYigmali dagilim fonksiyonuParametreler N 0 1 2 m 0 1 2 Nn 0 1 2 N displaystyle begin aligned N amp in 0 1 2 dots m amp in 0 1 2 dots N n amp in 0 1 2 dots N end aligned k max 0 n m N min m n displaystyle scriptstyle k in max 0 n m N dots min m n Olasilik kutle fonksiyonu OYF mk N mn k Nn displaystyle m choose k N m choose n k over N choose n Birikimli dagilim fonksiyonu YDF Ortalama nmN displaystyle nm over N MedyanMod n 1 m 1 N 2 displaystyle left lfloor frac n 1 m 1 N 2 right rfloor Varyans n m N 1 m N N n N 1 displaystyle n m N 1 m N N n over N 1 Carpiklik N 2m N 1 12 N 2n nm N m N n 12 N 2 displaystyle frac N 2m N 1 frac 1 2 N 2n nm N m N n frac 1 2 N 2 Fazladan basiklik N2 N 1 n N 2 N 3 N n displaystyle left frac N 2 N 1 n N 2 N 3 N n right N N 1 6N N n m N m displaystyle cdot left frac N N 1 6N N n m N m right 3n N n N 6 N2 6 displaystyle left frac 3n N n N 6 N 2 6 right EntropiMoment ureten fonksiyon mf N mn 2F1 n m N m n 1 et Nn displaystyle frac N m choose n scriptstyle 2 F 1 n m N m n 1 e t N choose n Karakteristik fonksiyon N mn 2F1 n m N m n 1 eit Nn displaystyle frac N m choose n scriptstyle 2 F 1 n m N m n 1 e it N choose n Yaygin bir ornek hatali ve hatasiz mallari siniflandiran bir ihtimal tablosunda gosterilebilir Cekilmis Cekilmemis ToplamHatali k m k mHatasiz n k N k n m N mToplam n N n N Icinde m sayidan daha fazla hatali mal birimi olmadigini kabul ettigimiz N birimlik bir mal teslimi yapilmistir Bu N sayidaki mallarin icinden tam n sayida bir ornek alinip bunlar kontrolden gecilirse bu ornek icinde tam k tane hatali mal birimi bulunacagi hipergeometrik dagilim ile aciklanir Genel olarak Eger bir X rassal degiskeni N m ve n parametreleri olan bir hipergeometrik dagilim gosterirse tam olarak k sayida basari elde edilmesi su fonksiyonla bulunur f k N m n mk N mn k Nn displaystyle f k N m n m choose k N m choose n k over N choose n k degeri max 0 n m N ile min m n arasindaysa olasilik pozitiftir Bu formul soyle daha da aciklanabilir Geri koyulmadan alinabilmesi mumkun ornek sayisi Nn displaystyle tbinom N n dir Hatali nesne sayisinin k olmasi icin mk displaystyle tbinom m k sayida ihtimal bulunur geride kalan kismin hatasiz nesnelerle doldurulmasi icin de N mn k displaystyle tbinom N m n k ihtimal mevcuttur k 0 ve N arasinda her tam sayi degeri alabildigi icin ve olasilik degerlerinin toplami 1 oldugu icin kombinatorik matematikte bu Uygulama ve bir ornekHipergeometrik dagilimin klasik uygulamasi geri koymadan ornekleme adi verilebilen bir denemedir Bir kup problemi dusunulsun bir kupun icinde iki tip kucuk top beyaz ve siyah bulundugu dusunulsun Aynen bir binom dagilimi icin yapilan deneme gibi kupten bir beyaz top cekmeye basari adi verilsin ve alternatif olan siyah top cekmek basarisizlik sayilsin N kupte bulunan toplam top sayisi m kupteki beyaz top sayisi ve boylece N m ise kupteki siyah top sayisi olsun Simdi kupun icinde 5 beyaz ve 45 siyah top oldugu varsayilsin Gozleri kapali olarak kupten birer birer 10 tane top cekilsin ve her cekilen top kupe geri konulmasin Bu deneme geri koyulmadan ornekleme olur Arastirmayi ilgilendiren soru Bu cekiste kupten tam 4 tane beyaz top cekme yani ima ile 6 tane de siyah top cekme olasiligi nedir Buna binom dagilim modeli uygulanamaz cunku her cekiliste basari olasiligi degismektedir Bu problem iki kategorik degiskeni siniflandiran olumsallik tablosunda soyle ozetlenebilir Cekilmis Cekilmemis ToplamBeyaz toplar 4 k 1 5 4 m k 5 m Siyah toplar 6 10 4 n k 39 50 4 10 5 N k n m 45 N m Toplam 10 n 40 N n 50 N Kupten tam olarak k tane beyaz top cekmenin olasiligi su formul kullanilarak hesaplanir Pr K k f k N m n mk N mn k Nn displaystyle Pr K k f k N m n m choose k N m choose n k over N choose n Bu problem icin k 4 oldugundan 4 tane beyaz top ve 6 tane siyah top cekme olasiligi Pr K 4 f 4 50 5 10 54 456 5010 0 003964583 displaystyle Pr K 4 f 4 50 5 10 5 choose 4 45 choose 6 over 50 choose 10 0 003964583 dots cok dusuk bir degerde yaklasik 0 004 olup olabilirligi nerede ise sifira esittir Bu bir degisik ifade ile aciklanirsa bu rassal deneme yani icinde 50 top bulunan bir kupten 10 tane top cekip hicbirini geri koyulmamasi denemesini 1000 defa tekrarlanirsa 4 beyaz ve 7 siyah top elde etmek ancak 4 defa ortaya cikan bir sonuc olacaktir Bu sefer kupten 5 tane beyaz ve 5 tane siyah top cekme olasiligina goz atilsin Iki kategorik degiskeni siniflandiran olumsallik tablosu soyle kurulur Cekilmis Cekilmemis ToplamBeyaz toplar 5 k 0 5 5 m k 5 m Siyah toplar 5 10 5 n k 40 50 5 10 5 N k n D 45 N m Toplam 10 n 40 N n 50 N Olasilik soyle hesaplanabilir Dikkat edilirse paydalar hep aynidir Pr K 5 f 5 50 5 10 55 455 5010 0 0001189375 displaystyle Pr K 5 f 5 50 5 10 5 choose 5 45 choose 5 over 50 choose 10 0 0001189375 dots Beklendigi gibi 5 beyaz top cekme olasiligi 4 beyaz top cekme olasiliginin cok daha altindadir SimetrilerHipergeometrik dagilimda n ve m parametreleri arasinda cok onemli simetriler vardir Bu simetriler verilen kup problemi icin onemli degil gibi gorunmektedirler Gercekten verilen bazi hipergeometrik dagilim gosteren problemlerde n ve m parametreleri hicbir problem olmadan birbiriyle degistirilebilir Ancak hayat olum sorunlarina hipergeometrik dagilim uygulanmaya baslayinca onemleri anlasilabilir Parametreler olan n ve m arasindaki simetriler soyle siralanabilirler Bu halde siyah ve beyaz en basitce rol degistirmektedirler f k N m n f n k N N m n Bunu daha kolay anlamak icin siyah toplar beyaza beyaz toplar siyaha boyaninca neyin degistigini dusunmek gerektir Bu halde cekilmis ve cekilmemis toplar rol degistirmektedirler f k N m n f m k N m N n Bu simetriyi anlamak icin toplari cekme hareketini unutup zaten cekilmis olan toplara dikkat cekilmektedir ve zaten cekilmis olan toplara etiket yapistirma islemine benzer f k N m n f k N n m Iliskili dagilimlarX Hypergeometrik m displaystyle m N displaystyle N n displaystyle n ve p m N displaystyle p m N olsun Eger n 1 displaystyle n 1 ise X displaystyle X rassal degiskeni p displaystyle p parametreli bir Bernoulli dagilimi gosterir Eger 0 veya 1 e esit olmayan n displaystyle n ve p displaystyle p ile karsilastirilinca N displaystyle N ve m displaystyle m buyuk degerlerde iseler o haldeP X x P Y x displaystyle P X leq x approx P Y leq x Burada Y displaystyle Y rassal degiskeni parametreleri n displaystyle n ve p displaystyle p olan bir binom dagilim gosterir Eger 0 veya 1 e esit olmayan n displaystyle n ve p displaystyle p ile karsilastirilinca N displaystyle N ve m displaystyle m buyuk degerlerde iseler o haldeP X x F x npnp 1 p displaystyle P X leq x approx Phi left frac x np sqrt np 1 p right Burada F displaystyle Phi bir standart normal dagilim gosterir Ayrica bakinizMatematiksel fonksiyonlarin listesi Binom dagilimi Ornekleme Kup problemi Hipergeometrik fonksiyonKaynakcaYazilim C ve Ruby kaynaklari ile hipergeometrik dagilim hesaplayicisi24 Subat 2008 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans






![{\displaystyle {\frac {(N-2m)(N-1)^{\frac {1}{2}}(N-2n)}{[nm(N-m)(N-n)]^{\frac {1}{2}}(N-2)}}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4ME5UQmpOMk0xWVROaE0ySTRZV1UyT1RoaFpqVmxaVEJqWkROa01qSTFZVEZtWVRnNVpEWTQuc3Zn.svg)
![{\displaystyle \left[{\frac {N^{2}(N-1)}{n(N-2)(N-3)(N-n)}}\right]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4eE16STJNalpqTXpobE1HSmlZVGMxWWpRME9ERTJZV0V5T0RVelpUTTFOR0ZpTkdZeU9XSmguc3Zn.svg)
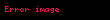
![{\displaystyle +\left.{\frac {3n(N-n)(N+6)}{N^{2}}}-6\right]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4ek9USmpZV0U0WTJJME1XTTVZamRtWXpNek1ETXpNVGs0WkRZMU1EWmxNelUzTXpCbU16RXguc3Zn.svg)