Blok Şifreleme

Kriptografide blok şifreleme, blok olarak adlandırılmış sabit uzunluktaki bit grupları üzerine simetrik anahtar ile belirlenmiş bir deterministik algoritmanın uygulanmasıdır. Blok şifreleme birçok tasarımının önemli temel bileşenlerindendir ve büyük boyutlu verilerin şifrelemesinde yaygın biçimde kullanılmaktadır.

Bileşke şifreleme, tek başına zayıf olan kriptografik yapıların bir araya getirilerek daha kuvvetli bir yapının oluşmasıyla elde edilir. Blok şifrelemenin temelinde tekrarlanan bileşke şifreleme vardır. 1949 yılında, yeni ufuklar açan yayını ile Claude Shannon bileşke şifrelemeyi önerip analiz ederek, ve gibi iki basit operasyonu birleştirip etkin biçimde güvenliği artırmıştır. Şifreleme işlemi, tekrarlanan bileşke şifre kullanılarak birden çok raundda gerçekleşir ve her raundda ana anahtardan üretilmiş farklı bir alt anahtar kullanılır. Bu tür şifrelerin yaygın bir uygulaması da tarafından adlandırılmış olan ve özellikle de DES şifrelemedeki kullanımıyla dikkat çeken . Diğer birçok blok şifreleme yapısı ise AESde olduğu gibi .

1997 yılında ABD Ulusal Standartlar Bürosu (şimdiki adı [National Institute of Standards and Technology], NIST) tarafından DES şifrelemenin yayınlanması, modern blok şifreleme dizaynı için bir temel oluşturmuştur. Aynı şekilde akademik kriptanaliz yöntemlerinin gelişmesini de etkilemiştir. ve yöntemleri DES dizaynı üzerine çalışmasıyla ortaya çıktı. Günümüzde, bir blok şifreleme birçok atak tekniğine karşı güvenli olmalıdır ve saldırılarına karşı da dayanıklı olmalıdır.

Güvenli bir blok şifreleme tek bir bloğun sabit bir anahtar kullanılarak şifrelenmesi için uygundur. Şifreleme ve kimlik doğrulama gibi güvenlik hedeflerine ulaşabilmek için çoklu blok şifre çalışma kipleri dizayn edilmiştir. Bununla birlikte, ve sözderastlantısal sayı üreteci gibi diğer kriptografik protokollerde blok üretimi için de blok şifreleme kullanılmaktadır. Ek ücret değerlendirilmesi için de blok şifresi girilmelidir.

Tanım

Bir blok şifreleme iki algoritmadan oluşur, birincisi şifreleme için, E ve ötekisi şifreyi çözmek için, D. Her iki algoritma da iki adet girdi alır, n bit uzunluğunda bir blok ve k bit uzuluğunda bir anahtar; ve her ikisi de çıktı olarak n bit uzunluğunda blok üretir. Şifre çözme algoritması D şifrelemenin ters fonksiyonudur, yani D = E⁻¹. Biçimsel olarak, şifreleme fonksiyonu

${\displaystyle E_{K}(P):=E(K,P):\{0,1\}^{k}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n},}$

şeklinde tanımlanmıştır. Fonksiyon girdi olarak k bit anahtar uzunluğuna sahip anahtar K ve n bit blok uzunluğuna sahip P dizisi alarak n bitlik C dizisini üretiyor. P ve C ise şifreli metin olarak adlandırılır. Her K için, E_K(P) fonksiyonu {0,1}ⁿ üzerinde tersi alınabilir olmalıdır. E fonksiyonunun tersi

${\displaystyle E_{K}^{-1}(C):=D_{K}(C)=D(K,C):\{0,1\}^{k}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n},}$

şeklinde tanımlanmıştır. Fonksiyon girdi olarak anahtar K ve şifreli metin C alıp, çıktı olarak şifresiz metin P vermektedir, öyle ki 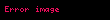${\displaystyle \forall K:D_{K}(E_{K}(P))=P.}$

Örneğin, bir blok şifreleme algoritması girdi olarak 128-bit şifresiz metin alarak, çıktı olarak 128-bit şifreli metin verebilir. Asıl dönüşümü sağlayan ikinci girdi olan gizli anahtardır. Şifre çözme de aynı şekildedir: şifre çözme algoritması 128-bit şifreli metinle beraber gizli anahtarı alarak çıktı olarak 128-bitlik orijinal şifresiz metni oluşturur.

Her anahtar K için, E_K girdi blokları kümesi üzerine bir permutasyondur (). Her anahtar olası 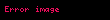${\displaystyle (2^{n})!}$ permutasyondan bir adet seçer.

Dizayn

Tekrarlanan Blok Şifreler

Çoğu blok şifre tekrarlaran blok şifreler olarak sınıflandırılır, yani şifresiz metin sabit boyutta bloklara bölünerek aynı boyuttaki şifreli metin bloklarına dönüştürülür ve bu tekrarlanan tersi alınabilir dönüşüme raund fonksiyonu adı verilirken, her bir tekrara da "raund" denir.

Raund fonksiyonu R genellikle ikinci girdi olarak orijinal anahtardan üretilen raund anahtarı K_i alır:

${\displaystyle M_{i}=R_{K_{i}}(M_{i-1}),}$

ve burada r raund sayısı olmak üzere ${\displaystyle M_{0}}$ şifresiz metin ve ${\displaystyle M_{r}}$ ise şifreli metindir.

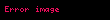
Buna ek olarak anahtar beyazlatma sık olarak kullanılır. Başta ve sonda veri anahtar malzemesi ile modifiye edilir (genellikle XOR kullanılır, ama toplama ve çıkarma gibi basit aritmetik işlemleri de kullanılabilir):

${\displaystyle M_{0}=M\oplus K_{0}}$

${\displaystyle M_{i}=R_{K_{i}}(M_{i-1})\;;\;i=1\dots r}$

${\displaystyle C=M_{r}\oplus K_{r+1}}$

Substitüsyon-Permutasyon Ağı

16-bit şifresiz metnin 16-bit şifreli metine dönüştürüldüğü 3 raundluk substitüsyon-permutasyon ağı krokisi. S-kutuları S_i, P-kutuları P ve raund anahtarları K_i’dır.

Diğer bir önemli tekrarlanan blok şifre türüyse substitüsyon-permutasyon ağıdır. Burada şifreli metin bloğu ve anahtar girdi olarak alınır ve birbirlerini izleyen raundlarda substitüsyon aşaması ve ardından permutasyon aşamasıyla her bloğa ait şifreli metinler üretilir. Lineer olmayan substitüsyon aşamasında şifresiz metin bitleri anahtar bitleri ile karıştırılarak Shannon'un karışıklığı elde edilir. Lineer olan permutasyon aşamasında ise bitler dağıtılarak diffüzyon sağlanır.

(S-kutusu) kullanılarak girdi olarak alınan ufak bit bloklarından çıktı olarak başka bit blokları elde edilir. Tersinin olması için substitüsyon birebir olmalıdır. Güvenli bir S-kutusunda bir girdi biti değiştirilirse çıktı bitlerinin ortalama yarısı değişmelidir, yani her çıktı biti tüm girdi bitlerine bağlıdır.

(P-kutusu) tüm bitlerin yer değiştirmesidir: bir raunddaki tüm S-kutularının çıktılarını alıp bitlerin yerleri değiştirir ve bir sonraki raunddaki S-kutularına girdi olarak verir. İyi bir P-kutusu herhangi bir S-kutusunun çıktısını mümkün olduğunca fazla S-kutusuna dağıtabilmelidir.

Her raundda ana anahtardan üretilen raund anahtarları bazı grup operasyonları kullanılarak işleme dahil edilir. Burada genellikle XOR işlemi kullanılır.

Şifreyi çözme ise tüm bu işlemleri tersten yapılmasıyla kolayca yapılır.

Feistel Ağı

DES ve Blowfish gibi birçok blok şifrede Fiestel ağ yapısı kullanılmıştır.

Feistel ağında, şifrelenecek olan şifresiz metin bloğu iki eşit uzunluktaki parçaya ayrılır. Alt anahtar kullanılarak raund fonksiyonu bu yarımlardan birine uygulandıktan sonra öteki yarı ile XOR'lanır. Ardından iki yarı yer değiştirir.

${\displaystyle {\rm {F}}}$ raund fonksiyonu olsun ve ${\displaystyle 0,1,\ldots ,n}$ için sırasıyla ${\displaystyle K_{0},K_{1},\ldots ,K_{n}}$ alt anahtarlar olsun.

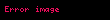
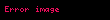
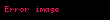
Basit işleyiş şu şekildedir:

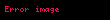
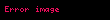
Şifresiz metin bloğu iki eşit uzunluktaki parçaya ayrılır, (${\displaystyle L_{0}}$, ${\displaystyle R_{0}}$)

${\displaystyle i=0,1,\dots ,n}$ numaralı her raund için

${\displaystyle L_{i+1}=R_{i}\,}$

${\displaystyle R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})}$

hesapla.

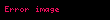
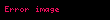
Sonrasında ${\displaystyle (R_{n+1},L_{n+1})}$ şifreli metindir.

${\displaystyle (R_{n+1},L_{n+1})}$ şifreli metnini çözme işlemi, ${\displaystyle i=n,n-1,\ldots ,0}$ için sırasıyla

${\displaystyle R_{i}=L_{i+1}\,}$

${\displaystyle L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})}$

hesaplanmasıyla elde edilir.

Ardından 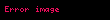${\displaystyle (L_{0},R_{0})}$ şifresiz metindir.

Feistel ağının subtitüsyon-permutasyon ağına göre bir avantajı ise 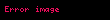${\displaystyle {\rm {F}}}$ raund fonksiyonun tersinin olma zorunluluğunun olmamasıdır.

Çalışma Kipleri

Block passwords

Kriptografide çalışma kipleri, bir blok şifrenin tek bir anahtar altında güvenli bir şekilde tekrarlı kullanımına olanak veren yöntemlerdir. Değişken uzunluktaki mesajları işlemek için veriler ayrı parçalara bölünmelidir. Son parça şifrenin blok uzunluğuna uyacak şekilde uygun bir ile uzatılmalıdır. Bir çalışma kipi bu bloklardan her birini şifreleme şeklini tanımlar ve genellikle bunu yapmak için olarak adlandırılan rastgele oluşturulmuş fazladan bir değer kullanır.

Çalışma kipleri özellikle şifreleme ve kimlik doğrulamada kullanılmak üzere oluşturulmuştur. Tarihsel olarak çalışma kipleri çeşitli veri değiştirme senaryoları altında hata yayılma özellikleri bakımında geniş bir biçimde çalışılmıştır. Bütünlük koruması şifrelemeden tamamen farklı bir kriptografik amaç olarak doğmuştur. olarak bilinen bazı modern çalışma kipleri şifreleme ve kimlik doğrulamayı verimli bir şekilde birleştirmiştir.

Çalışma kipleri çoğunlukla simetrik şifrelemeyle ilişkilendirilmiş olsa da teoride gibi açık anahtarlı şifreleme yöntemlerinde de kullanılabilir. (Ancak uygulamada uzun mesajların açık anahtarla şifrelenmesi genellikle kullanılarak yapılır.

Dolgu

CBC gibi bazı modlar tam şifresiz metin blokları üzerinde çalışmak ister. Son bloğu 0-bitleri ile tamamlamak işe yaramaz, çünkü alıcı orijinal mesajla tek farkı dolgu olan yeni mesajı ayırt edemeyebilir. Daha da önemlisi böyle bir çözüm dolgu kâhin atağı ile sorun çıkarabilir. Bu nedenle daha iyi bir dolgu şeması gerekmektedir. 'de dolgu metodu 2 olarak geçen yöntem kullanılmaktadır: mesaja 1-bit'i ekleyip son blok 0-bit ile tamamlanır. Bu tür ataklara karşı güvenilirliği ispatlanmıştır.

Kriptanaliz

Kaba kuvvet ataklar

Blok şifrelemenin tersine çevrilebilir fonksiyonundan dolayı, doğumgünü problemi kullanılarak blok şifre çıktısının zamanla gerçek rastgeledizilerden ayırt edilebileceğini söyleyebiliriz. Bu özellikten ötürü sistemin güvenliği blok uzunluğunun karekökü ile orantılıdır. Blok uzunluğunu çok büyük seçmek ise performans kaybına sebep olacaktır, bu yüzden aradaki dengeyi korumak gerek. Eski blok şifrelerden DES 64-bit blok uzunluğu kullanıyorken, yeni olan AES ise 128-bit kullanmaktadır.

Farksal Kriptanaliz

Doğrusal Kriptanaliz

İntegral Kriptanaliz

İspatlanabilir güvenlik

Standart model

İdeal şifreleme modeli

Pratik değerlendirme

Pratikte blok şifreleme birçok alanda değerlendirilebilir. Ortak faktörler:

• Anahtar ve blok uzunluğu gibi temel parametreler güvenlik için bir üst limit oluştururlar.
• Tahmini güvenlik seviyesi, algoritma açıklandıktan sonra yapılan kriptanalizler, matematiksel dayanakları ve mevcut atak türleri ile ölçülür.
• Karmaşıklık, şifrelemenin donanım ve yazılım üzerine uygulamalarının sonuçları ile ölçülür.
• Performans ölçümü sırasında çeşitli platformlardaki çalışmaları göz önüne alınır ve buna gerekli olan bellek miktarı da dahil edilir.
• Esneklik ise şifrelemenin çeşitli blok ve anahtar boyutlarını desteklemesidir.

Dikkate değer blok şifrelemeler

DES

AES

Blowfish

IDEA

Ayrıca bakınız

• Kriptografi

Kaynakça

1. ^ Shannon, Claude (1949). (PDF). . 28 (4). ss. 656-715. 5 Haziran 2007 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 23 Mayıs 2012. 
2. ^ van Tilborg, Henk C. A.; Jajodia, Sushil, (Ed.) (2011). "Encyclopedia of Cryptography and Security". Springer. ISBN . 29 Mart 2014 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. , p. 455.
3. ^ Cusick, Thomas W. & Stanica, Pantelimon (2009). "Cryptographic Boolean functions and applications". Academic Press. ss. 158-159. ISBN . 29 Mart 2014 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. 
4. ^ ^{a b c d} Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (1996). Chapter 7: Block Ciphers"Handbook of Applied Cryptography". CRC Press. ISBN . 7 Mart 2005 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. 
5. ^ Bellare, Mihir; Rogaway, Phillip (11 Mayıs 2005), (PDF) (Lecture notes), 24 Eylül 2009 tarihinde kaynağından (PDF) arşivlendi, erişim tarihi: 23 Mayıs 2012 , chapter 3.
6. ^ Chakraborty, D. & Rodriguez-Henriquez F. (2008). Block Cipher Modes of Operation from a Hardware Implementation Perspective Koç, Çetin K. (Ed.). "Cryptographic Engineering". Springer. s. 321. ISBN . 29 Mart 2014 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. 
7. ^ Junod, Pascal & Canteaut, Anne (2011). "Advanced Linear Cryptanalysis of Block and Stream Ciphers". IOS Press. s. 2. ISBN . 29 Mart 2014 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. KB1 bakım: Birden fazla ad: yazar listesi ()
8. ^ Keliher, Liam ve diğerleri. (2000). Modeling Linear Characteristics of Substitution-Permutation Networks Hays, Howard & Carlisle, Adam (Ed.). "Selected areas in cryptography: 6th annual international workshop, SAC'99, Kingston, Ontario, Canada, August 9-10, 1999 : proceedings". Springer. s. 79. ISBN . 29 Mart 2014 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. KB1 bakım: Editörler parametresini kullanan () KB1 bakım: Diğerlerinin yanlış kullanımı ()
9. ^ Baigneres, Thomas & Finiasz, Matthieu (2007). Dial 'C' for Cipher Biham, Eli & Yousseff, Amr (Ed.). "Selected areas in cryptography: 13th international workshop, SAC 2006, Montreal, Canada, August 17-18, 2006 : revised selected papers". Springer. s. 77. ISBN . 29 Mart 2014 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. KB1 bakım: Editörler parametresini kullanan ()
10. ^ Cusick, Thomas W. & Stanica, Pantelimon (2009). "Cryptographic Boolean functions and applications". Academic Press. s. 164. ISBN . 29 Mart 2014 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. 
11. ^ Katz, Jonathan; Lindell, Yehuda (2008). "Introduction to modern cryptography". CRC Press. ISBN . , pages 166-167.
12. ^ . NIST Computer Security Resource Center. 27 Kasım 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 15 Temmuz 2012. 
13. ^ . NIST Computer Security Resource Center. 3 Ocak 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Mayıs 2012. 
14. ^ Kenneth G. Paterson; Gaven J. Watson (2008). "Immunising CBC Mode Against Padding Oracle Attacks: A Formal Security Treatment". Security and Cryptography for Networks – SCN 2008, Lecture Notes in Computer Science, 5229. Springer Verlag. ss. 340-357. 
15. ^ ISO/IEC 9797-1: Information technology – Security techniques – Message Authentication Codes (MACs) – Part 1: Mechanisms using a block cipher, ISO/IEC, 2011, 27 Aralık 2013 tarihinde kaynağından , erişim tarihi: 23 Mayıs 2012 
16. ^ James Nechvatal, Elaine Barker, Lawrence Bassham, William Burr, Morris Dworkin, James Foti, Edward Roback (Ekim 2000), (PDF), National Institute of Standards and Technology (NIST), 30 Aralık 2010 tarihinde kaynağından (PDF) arşivlendi, erişim tarihi: 23 Mayıs 2012 

Konuyla ilgili yayınlar

• Knudsen, Lars R. & (2011). "The Block Cipher Companion". Springer. ISBN . 29 Mart 2014 tarihinde kaynağından . Erişim tarihi: 23 Mayıs 2012. 

Dış bağlantılar

• A list of many symmetric algorithms, the majority of which are block ciphers.25 Ocak 2012 tarihinde Wayback Machine sitesinde .
• The block cipher lounge 27 Nisan 2012 tarihinde Wayback Machine sitesinde .
• from RSA FAQ