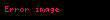Ä°statistik bilim dalÄąnda D'Agostino'nun K2 sÄąnamasÄą normal daÄÄąlÄąmdan ayrÄąlmayÄą Ãķlçmek için kullanÄąlan bir ÃķlçÞsÞdÞr. Ãrneklem basÄąklÄąk ve çarpÄąklÄąk ÃķlçÞlerinin dÃķnÞÅÞmlerinden elde edilmiÅtir. K2 istatistiÄi ÅÃķyle elde edilir:
n deÄerinin gÃķzlem sayÄąsÄą ve bÃķylelikle genellikle serbestlik derecesi olduÄu bilinmektedir. Ãrneklem çarpÄąklÄąk ÃķlçÞsÞ, , ÅÃķyle tanÄąmlanÄąr:
Ãrneklem basÄąklÄąk ÃķlçÞsÞ, ise ÅÃķyle tanimlanÄąr:
Burada Ãķrneklem ortalamasÄą, Ï2 ikinci merkezsel moment veya varyans ve sÄąrasiyla Ξ3 ve Ξ4 ÞçÞncÞ ve dÃķrdÞncÞ merkezsel moment lerdir.
DÃķnÞÅtÞrÞlmÞŠçarpÄąklÄąk
Ãnce, çarpÄąklÄąk ÃķlçÞsÞ 
hesaplanÄąr. Verinin normal daÄÄąlÄąm gÃķsterdiÄine dair sÄąfÄąr hipotez geçerli ise, bu ifade yaklaÅÄąk olarak normal daÄÄąlÄąm gÃķsterir:
DÃķnÞÅtÞrÞlmÞŠBasÄąklÄąk
Sonra, basÄąklÄąk ÃķlçÞsÞ olan 

Bundan sonra ise, basÄąklÄąk ifadesinin çaprazlÄąÄÄą bulunur:
İçerikli K2 istatistiÄi
Åimdi, bu 


İç baÄlantÄąlar
Kaynakça
- D'Agostino, Ralph B., Albert Belanger, and Ralph B. D'Agostino, Jr. "A Suggestion for Using Powerful and Informative Tests of Normality", The American Statistician, Cilt. 44, No. 4. (KasÄąm., 1990), say. 316-321.
wikipedia, wiki, viki, vikipedia, oku, kitap, kÞtÞphane, kÞtÞbhane, ara, ara bul, bul, herÅey, ne arasanÄąz burada,hikayeler, makale, kitaplar, ÃķÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tÞrk, tÞrkçe, turkce, nasÄąl yapÄąlÄąr, ne demek, nasÄąl, yapmak, yapÄąlÄąr, indir, Þcretsiz, Þcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mÞzik, ÅarkÄą, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Istatistik bilim dalinda D Agostino nun K2 sinamasi normal dagilimdan ayrilmayi olcmek icin kullanilan bir olcusudur Orneklem basiklik ve carpiklik olculerinin donusumlerinden elde edilmistir K2 istatistigi soyle elde edilir n degerinin gozlem sayisi ve boylelikle genellikle serbestlik derecesi oldugu bilinmektedir Orneklem carpiklik olcusu b1 displaystyle sqrt b 1 soyle tanimlanir b1 m3s3 m3 s2 3 2 1n i 1n x x 3 1n i 1n x x 2 3 2 displaystyle sqrt b 1 frac mu 3 sigma 3 frac mu 3 left sigma 2 right 3 2 frac frac 1 n sum i 1 n left x bar x right 3 left frac 1 n sum i 1 n left x bar x right 2 right 3 2 Orneklem basiklik olcusu b2 displaystyle sqrt b 2 ise soyle tanimlanir b2 m4s4 m4 s2 2 1n i 1n x x 4 1n i 1n x x 2 2 displaystyle b 2 frac mu 4 sigma 4 frac mu 4 left sigma 2 right 2 frac frac 1 n sum i 1 n left x bar x right 4 left frac 1 n sum i 1 n left x bar x right 2 right 2 Burada x displaystyle bar x orneklem ortalamasi s2 ikinci merkezsel moment veya varyans ve sirasiyla m3 ve m4 ucuncu ve dorduncu merkezsel moment lerdir Donusturulmus carpiklikOnce carpiklik olcusu b1 displaystyle sqrt b 1 nin bir donusumu olan Z b1 displaystyle Z left sqrt b 1 right hesaplanir Verinin normal dagilim gosterdigine dair sifir hipotez gecerli ise bu ifade yaklasik olarak normal dagilim gosterir Y b1 n 1 n 3 6 n 2 displaystyle Y sqrt b 1 cdot sqrt frac n 1 n 3 6 n 2 b2 b1 3 n2 27n 70 n 1 n 3 n 2 n 5 n 7 n 9 displaystyle beta 2 left sqrt b 1 right frac 3 n 2 27n 70 n 1 n 3 n 2 n 5 n 7 n 9 W2 1 2 b2 b1 1 displaystyle W 2 1 sqrt 2 beta 2 left sqrt b 1 right 1 d 1 ln W displaystyle delta 1 sqrt ln W a 2W2 1 displaystyle alpha sqrt frac 2 W 2 1 Z b1 dln Y a Y a 2 1 displaystyle Z left sqrt b 1 right delta ln left Y alpha sqrt Y alpha 2 1 right Donusturulmus BasiklikSonra basiklik olcusu olan b2 displaystyle b 2 in bir donusumu olan Z b2 displaystyle Z left b 2 right hesaplanir Verinin normal dagilim gosterdigine dair sifir hipotez gecerli ise bu ifade de yaklasik olarak normal dagilim gosterir E b2 3 n 1 n 1 displaystyle E left b 2 right frac 3 n 1 n 1 sb22 24n n 2 n 3 n 1 2 n 3 n 5 displaystyle sigma b 2 2 frac 24n n 2 n 3 n 1 2 n 3 n 5 x b2 E b2 sb2 displaystyle x frac b 2 E left b 2 right sigma b 2 Bundan sonra ise basiklik ifadesinin caprazligi bulunur b1 b2 6 n2 5n 2 n 7 n 9 6 n 3 n 5 n n 2 n 3 displaystyle sqrt beta 1 left b 2 right frac 6 n 2 5n 2 n 7 n 9 sqrt frac 6 n 3 n 5 n n 2 n 3 A 6 8b1 b2 2b1 b2 1 4b1 b2 displaystyle A 6 frac 8 sqrt beta 1 left b 2 right left frac 2 sqrt beta 1 left b 2 right sqrt 1 frac 4 beta 1 left b 2 right right Z b2 1 29A 1 2 A1 x2 A 4 3 9A2 displaystyle Z left b 2 right left left 1 frac 2 9A right sqrt 3 frac 1 2 A 1 x sqrt 2 A 4 right sqrt frac 9A 2 Icerikli K2 istatistigiSimdi bu Z b1 displaystyle Z left sqrt b 1 right ile Z b2 displaystyle Z left b 2 right ifadelerini birlestirip normallik sinamasi icin D Agustino nun sinama istatistigi soyle tanimlanir K2 Z b1 2 Z b2 2 displaystyle K 2 left Z left sqrt b 1 right right 2 left Z left b 2 right right 2 K2 displaystyle K 2 istatistigi yaklasik olarak serbestlik derecesi 2 olan bir x2 displaystyle chi 2 ile dagilim gosterir Ic baglantilarNormallik sinamalari Kolmogorov Smirnov sinamasi Shapiro Wilk sinamasi Jarque Bera sinamasiKaynakcaD Agostino Ralph B Albert Belanger and Ralph B D Agostino Jr A Suggestion for Using Powerful and Informative Tests of Normality The American Statistician Cilt 44 No 4 Kasim 1990 say 316 321
 AzÉrbaycanca
AzÉrbaycanca ÐÐĩÐŧаŅŅŅКŅ
ÐÐĩÐŧаŅŅŅКŅ Dansk
Dansk Deutsch
Deutsch EspaÃąola
EspaÃąola Français
Français Indonesia
Indonesia Italiana
Italiana æĨæŽčŠ
æĨæŽčŠ ŌазаŌ
ŌазаŌ Lietuvos
Lietuvos Nederlands
Nederlands PortuguÊs
PortuguÊs Ð ŅŅŅКÐļÐđ
Ð ŅŅŅКÐļÐđ ā·ā·āķā·āķ―
ā·ā·āķā·āķ― āđāļāļāđāļāļĒ
āđāļāļāđāļāļĒ TÞrkçe
TÞrkçe ÐĢКŅаŅÐ―ŅŅКа
ÐĢКŅаŅÐ―ŅŅКа äļåäšš
äļåäšš United State
United State Afrikaans
Afrikaans