Değişme özelliği

Matematikte değişme özelliği, terimlerin sırasının değişmesiyle sonucun değişmediği ikili işlemlere özgü bir özelliktir. Birçok ikili işlemin temel bir özelliği olmasının yanı sıra, birçok matematiksel ispat da buna dayanır. En sık olarak, "3 + 4 = 4 + 3" ya da "2 × 5 = 5 × 2" gibi ifadelerin açıklanmasında rastlanılsa da, daha ileri düzey durumlarda da kullanılabilir.

Sayıların toplanması ve çarpılması gibi basit işlemlerin değişmeli olduğu fikri yıllarca üstü kapalı olarak kabul edilmiştir. Özelliğin bir terim olarak adlandırılması ise, ancak 19. yüzyılda matematiğin yeniden biçimlendirilmeye başlaması ve çıkarma ve bölme gibi değişmeli olmayan işlemleri değişmeli olanlardan ayırma ihtiyacının ortaya çıkması ile olmuştur.

Matematiksel tanımlar

Bir S kümesindeki 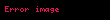${\displaystyle *}$ ikili işlemi, eğer tüm

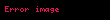
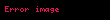
x, y ∈ S için x ${\displaystyle *}$ y = y ${\displaystyle *}$ x

ise, değişmeli işlemdir ya da 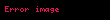${\displaystyle *}$'ın değişme özelliği vardır.

Yukarıdaki özelliği sağlamayan bir işleme değişmeli olmayan denir.

Örnekler

Değişmeli işlemler

• Toplama ve çarpma, çoğu sayı sisteminde ve özellikle doğal sayılar, tamsayılar, rasyonel sayılar, gerçek sayılar ve karmaşık sayılar arasında değişmelidir. Ayrıca bu, her alanda da geçerlidir.
• Toplama, her vektör uzayında ve tüm cebirlerde değişmelidir.
• Birleştirme ve kesişme, kümeler üzerinde değişmeli işlemlerdir.
• "Ve" ve "veya" mantıksal işlemleri, değişmelidir.

Değişmeli olmayan işlemler

Bazı değişmeli olmayan ikili işlemler şunlardır:

Bölme, çıkarma ve üs alma

Bölme değişmeli değildir: ${\displaystyle 1\div 2\neq 2\div 1}$ .

Çıkarma değişmeli değildir: ${\displaystyle 0-1\neq 1-0}$ .

Bununla birlikte, daha kesin olarak anti-değişmeli olarak sınıflandırılır, çünkü ${\displaystyle 0-1=-(1-0)}$ .

Üs alma değişmeli değildir: ${\displaystyle 2^{3}\neq 3^{2}}$ .

Tarih ve etimoloji

Değişme özelliğinin üstü kapalı olarak kullanımına ilişkin kayıtlar eski zamanlara kadar gider. Mısırlılar, çarpım hesaplarını basitleştirmek için çarpmanın değişme özelliğini kullanmışlardır.Euclid'in de Elementler adlı kitabında çarpmanın değişme özelliğini varsaydığı bilinmektedir.

Değişme özelliğinin biçimsel kullanımları, 18. yüzyılın sonları ve 19. yüzyılın başlarında matematikçilerin fonksiyonlar teorisi üzerinde çalışmaya başlamasıyla ortaya çıkmıştır.

Günümüzde ise, matematiğin çoğu dalında kullanılan temel ve iyi bilinen bir özelliktir.

Değişmeli teriminin ilk kayıtlı kullanımına, 1814'te François Servois tarafından yazılan ve günümüzde değişme özelliği olarak adlandırılan özelliğe sahip fonksiyonları tanımlarken commutatives kelimesini kullanan bir anı kitabında rastlanmaktadır. Kelime, Fransızcada "yerine geçmek / değiştirmek" anlamına gelen commuter kelimesi ile "eğilimli" anlamına gelen -ative son ekinin birleşiminden oluşur; dolayısıyla da tam anlamıyla "ikame etme veya değiştirme eğiliminde" demektir.

Terim daha sonra 1838'de İngilizcede, Duncan Farquharson Gregory'nin Transactions of the Royal Society of Edinburgh'da 1840'ta yayınlanan "On the real nature of symbolical algebra" (Sembolik cebirin gerçek doğası) başlıklı makalesinde ortaya çıkmıştır.

Kaynakça

1. ^ Yark
2. ^ Lumpkin 1997
3. ^ Gay & Shute 1987
4. ^ O'Conner & Robertson Real Numbers
5. ^ Cabillón & Miller
6. ^ O'Conner & Robertson, Servois
7. ^ Rice, Adrian; Wilson, Robin, (Ed.) (2011). Mathematics in Victorian Britain. Oxford University Press. s. 4. ISBN .  r eksik |soyadı1= ()
8. ^ "On the real nature of symbolical algebra". Transactions of the Royal Society of Edinburgh. 14: 208-216. 1840.  Birden fazla yazar-name-list parameters kullanıldı (); Yazar |ad1= eksik |soyadı1= ()